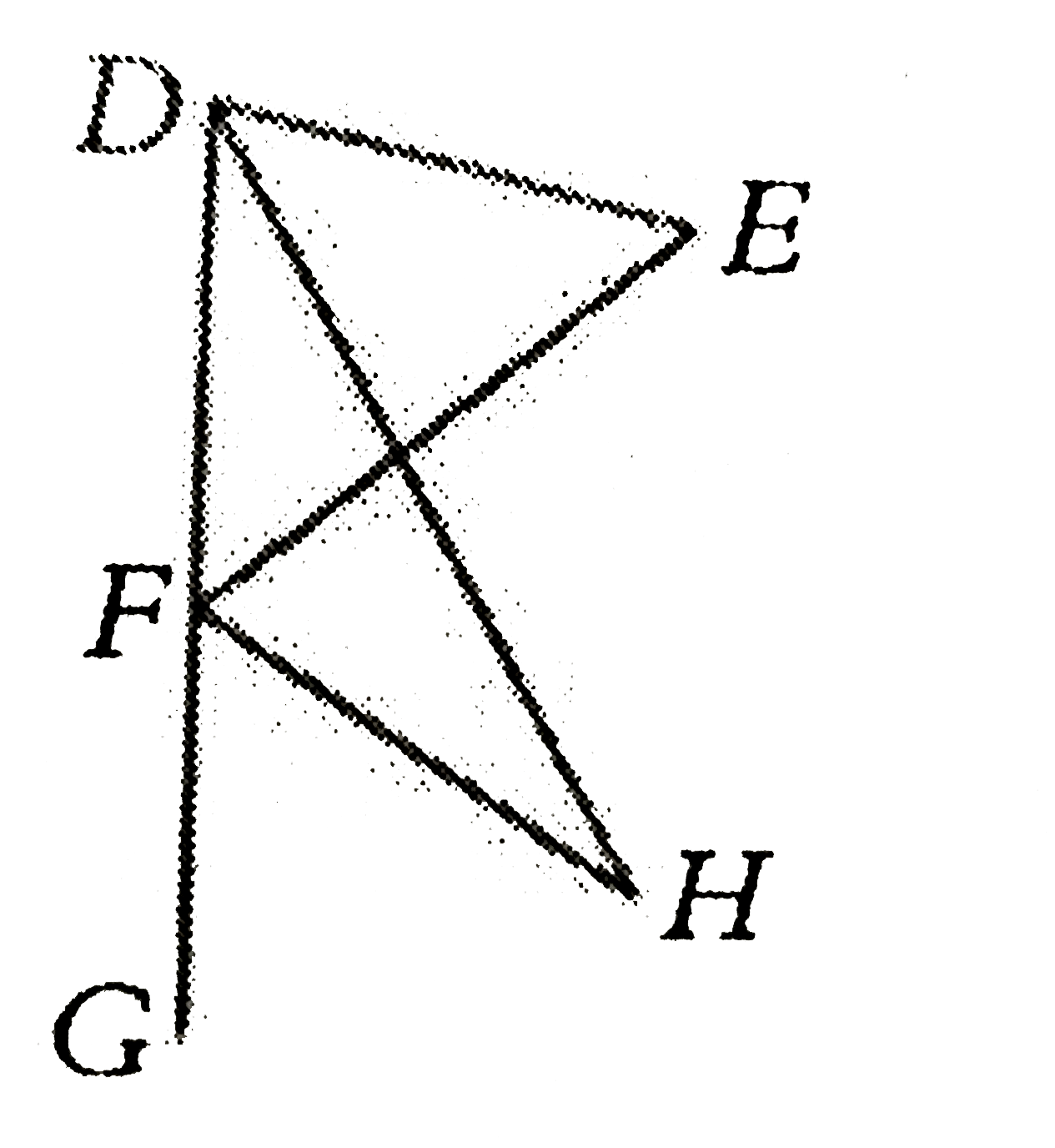
In the abve figure, DEF is a triangle whose side DF is produced to G. HF and HD are the bisectors of ∠EFG and ∠EDG respectively . If ∠DEF=2312.∘ and ∠DHF ( in degrees) =
1112
1125
1134
1113
The correct Answer is:c
(i) DH and FH are angle bisectors. Exterior angle of a triangle equals the sum of its interior opposite anges.
(ii) Take ∠FDH=∠HDE=x and ∠EFH=∠HFG=y.
(iii) ∠EFG is the exterior angle of a ΔDEF.
(iv) ∠DEF=2312.∘ and 2x+y=180∘−2312.∘
(v) Find x and y and H.
∴2y=2x+2312
Simplify to obtain the value of the required angle.
Topper's Solved these Questions
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level 3
Explore 7 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:TEST YOUR CONCEPTS ( VERY SHORT ANSWER TYPE QUESTIONS)
Explore 28 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level 1
Explore 32 Videos
- FormulaeBook:PEARSON IIT JEE FOUNDATIONChapter:FormulaeExercise:Level 3
Explore 7 Videos
- INDICESBook:PEARSON IIT JEE FOUNDATIONChapter:INDICESExercise:CONCEPT APPLICATION (Level 3)
Explore 7 Videos
Similar Questions
In the given figure, ΔABC is an equilateral triangle whose side BC has been produced in both the directions to D and E respectively. Prove that ∠ACD=∠ABE.
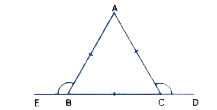
View SolutionThe sides AB and AC of a ΔABC are produced to P and Q respectively. If the bisectors of ∠PBC and ∠QCB meet at O ; Then ∠BOC=90∘−12∠A
View Solution
Knowledge Check

In the above figure , DEF is a triangle whose side DF is produced to G .HF and HD are the bisectors of ∠EFGand∠EDG , respectively . If ∠DEF=231(2)∘ , then ∠DHF (in degrees) = _______.A1112B1125C1134D1113In ΔPQR,PD⊥QR and PO is the bisector of ∠QPR. If ∠PQR=65∘ and ∠PRQ=2312.∘ then ∠DPO in degrees =
A2034B2012C2015D2014In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQRand ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
A50B60C80D100
ΔABC~ΔDEF in which AX and DY are the bisectors of ∠Aand∠D respectively . If AX=6.5cmandDY=5.2cm, find the ratio of the areas of ΔABCandΔDEF.
View SolutionIn the given figure, OD and OE are bisectors of ΔCDE and ΔDEB respectively. Find the measures of <1, <2,<3,<4
View SolutionIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of <PBC and <QCB intersect at O. Tnen. <BOC is equal to
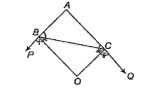
View SolutionIn triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQR and ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
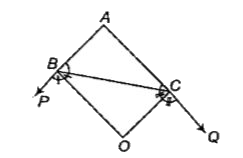
View SolutionIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
View Solution
