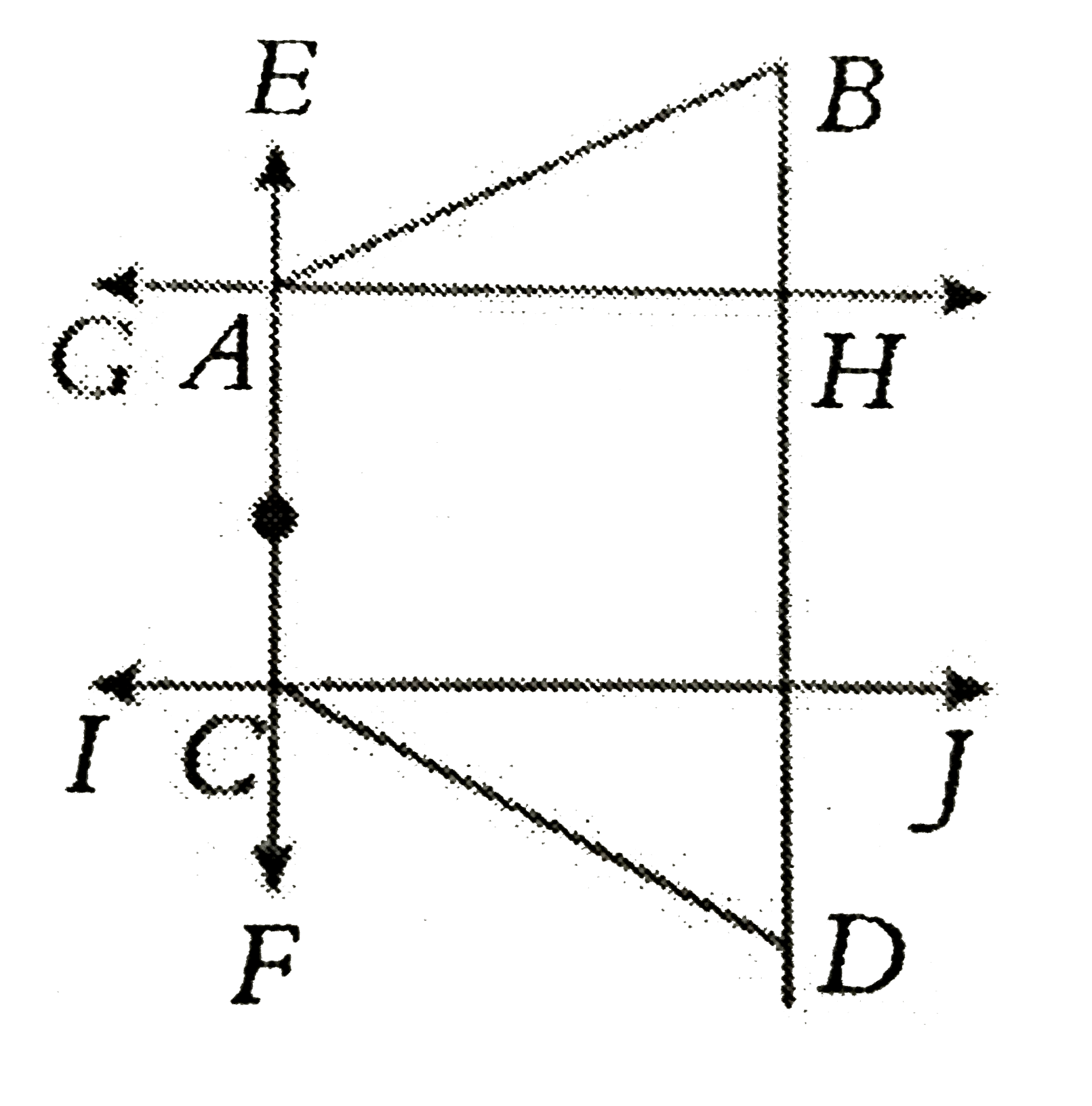
In the above figure, GH∣∣IJ and AC∣∣BD,AB and CD are bisectors of ∠EAH and ∠FCJ respectively. Find the ∠ABD+∠BDC, if ∠BAC=3∠BDC.
A
80∘
B
90∘
C
100∘
D
110∘
Video Solution
Text Solution
The correct Answer is:b
(i) Sum of the angles in a straight line is 180∘. Vertically opposite angles are equal. Co-interior angles are supplementary .
(ii) Let ∠FCD=∠DCJ=x∘ and ∠EAB=∠BAH=y∘.
(iii) ∠BDC=∠DCF (alterante angles ) and ∠BAC=3∠BDC (1) (given)
(iv) ∠ACJ=(180∘)=(180∘−2x∘)
∴∠HAC=∠EAH (2)
(vi) Solve equations (1) and (2) .
|
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 3
7 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - TEST YOUR CONCEPTS ( VERY SHORT ANSWER TYPE QUESTIONS)
28 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 1
32 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
Knowledge Check

In the above figure, GH∣∣IJ and AC∣∣BD,AB and CD are bisectors of ∠EAH and ∠FCJ respectively. Find the ∠ABD+∠BDC, if ∠BAC=3∠BDC.A80∘B90∘C100∘D110∘In the given figure AB||CD||EF and GH||KL Find m ∠HKL.
 A85∘B145∘C120∘D95∘
A85∘B145∘C120∘D95∘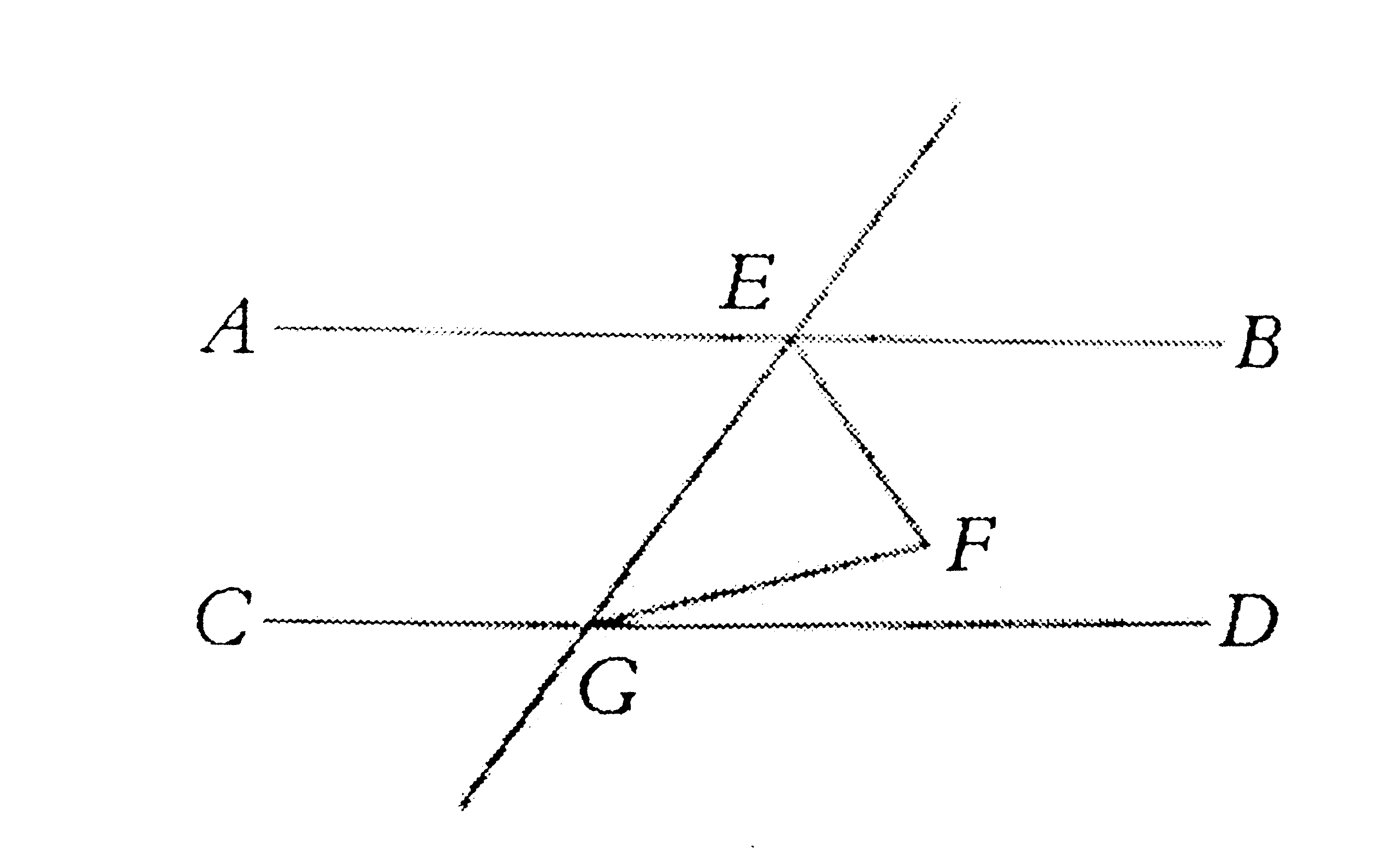
In the figure above, AB || CD. EF and FG are the bisectors of ∠BEGand∠DGE, respectively. ∠FEG=∠FGE+10∘. Find ∠FGE.A20∘B25∘C40∘D35∘
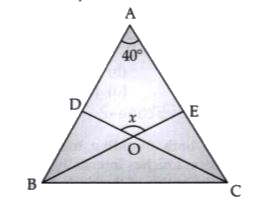
In the given figure , AB = AC , ∠BAC=40∘ , BE and CD are angle bisectors of ∠Band∠C respectively . If ∠DOE=x , the value of x is :
View Solution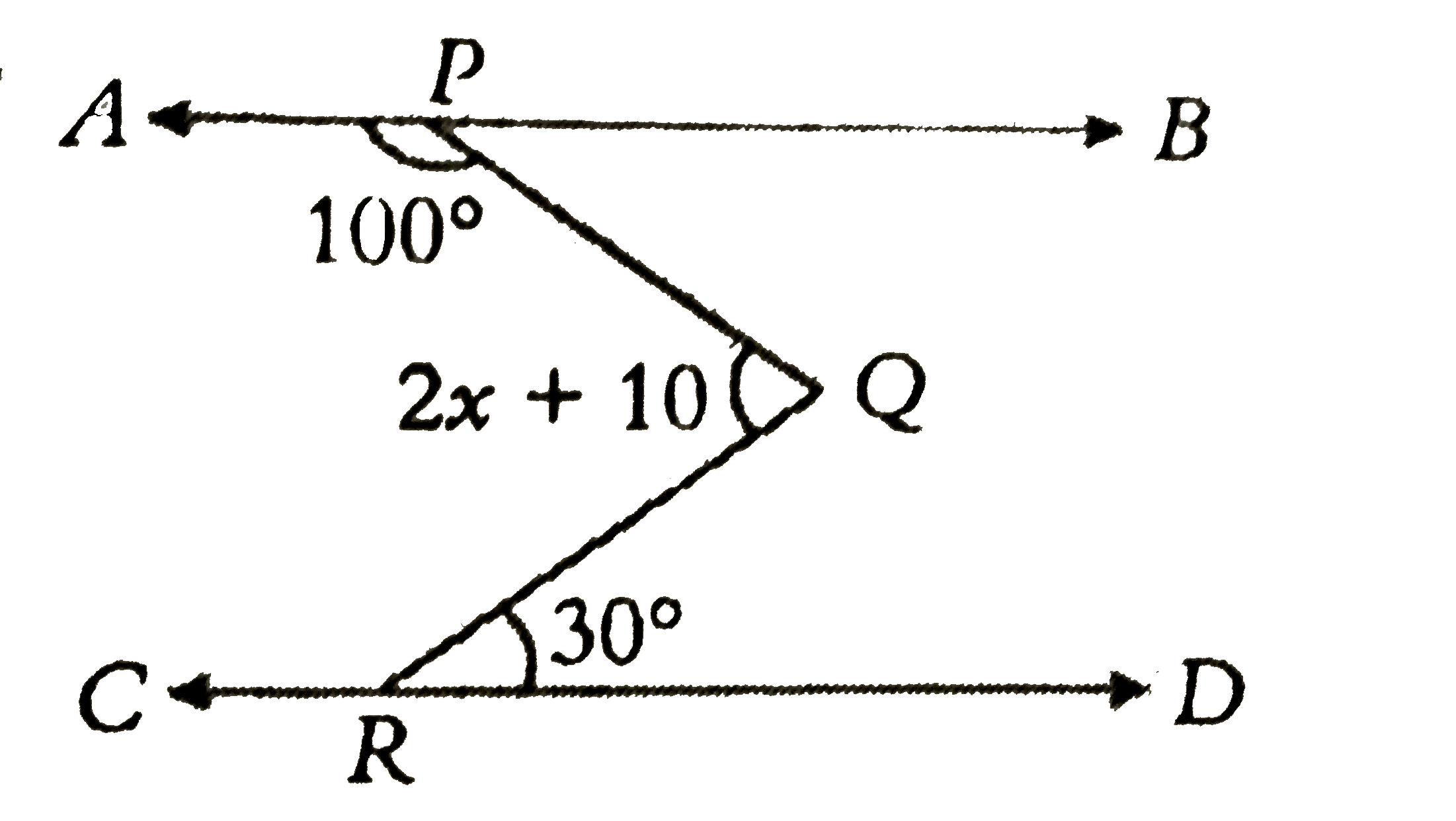
In the above figure, AB is parallel to CD. P and R are the points on AB and CD respectively. Q is in between AB and CD. Find the value of x in degrees
View Solution
In the figure above, AB || CD. EF and FG are the bisectors of ∠BEGand∠DGE, respectively. ∠FEG=∠FGE+10∘. Find ∠FGE.
View Solution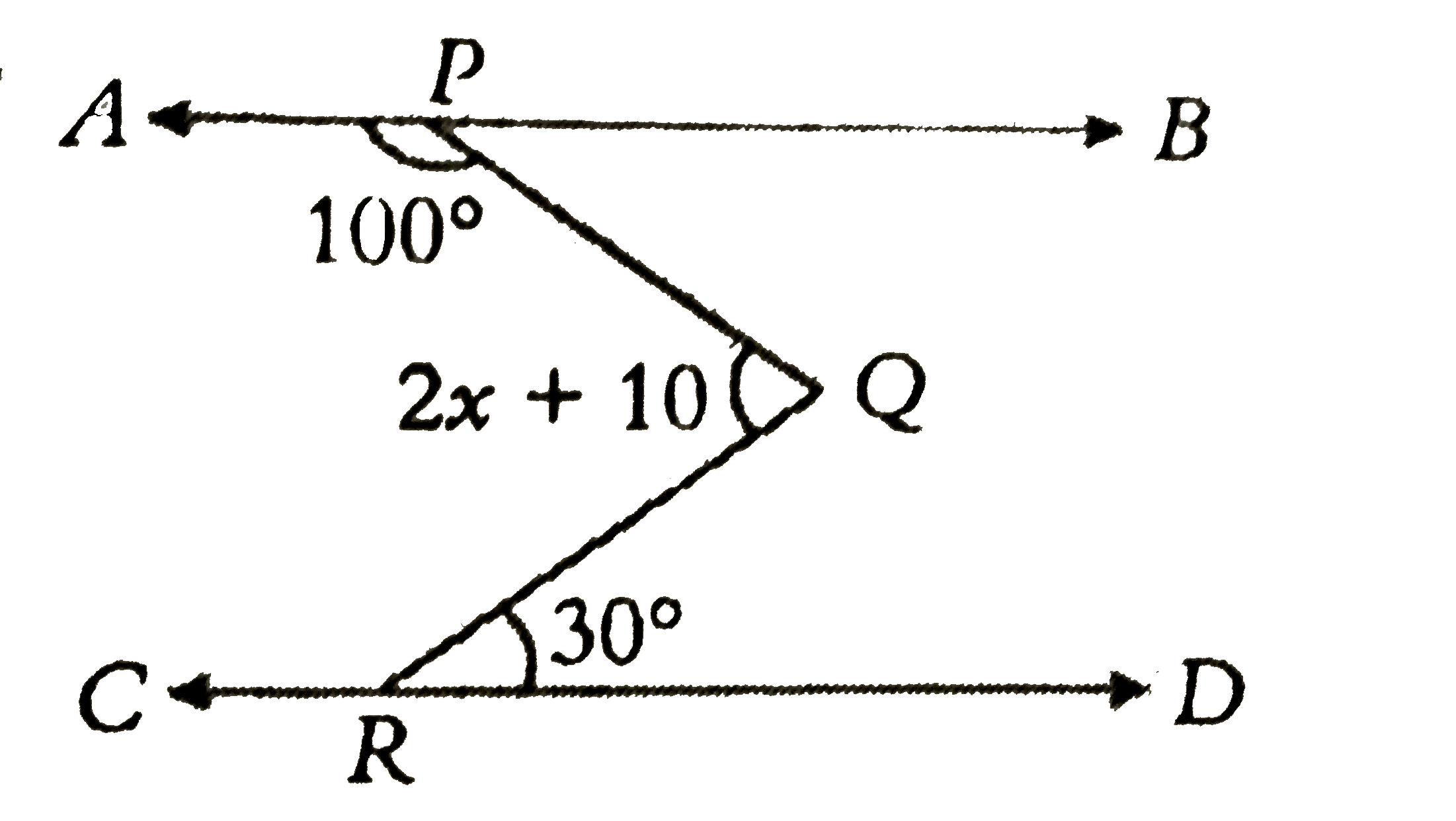
In the above figure, AB is parallel to CD. P and R are the points on AB and CD respectively. Q is in between AB and CD. Find the value of x in degrees
View SolutionIn the given figure below, if AC = BD then prove that AB = CD.

View Solution

