In the adjacent figure, if AB=12cm, BC=8cm and AC=10cm , then AD= (FIGURE) (a) 5cm (b) 4cm (c) 6cm (d) 7cm
To solve the problem, we need to find the length of segment AD in the given triangle ABC, where AB = 12 cm, BC = 8 cm, and AC = 10 cm. We will use the properties of tangents from a point outside a circle.
1. Identify the Tangents:
From point A, we can draw two tangents to the circle, which we will denote as AD and AF. According to the properties of tangents, the lengths of tangents drawn from an external point to a circle are equal. Therefore, we have:
AD=AF
Let's denote AD=AF=x.
2. Identify Other Tangent Segments:
Similarly, from point B, we can draw two tangents to the circle, denoting them as BD and BE. We will denote BD=BE=y.
From point C, we can draw two tangents to the circle, denoting them as CE and CF. We will denote CE=CF=z.
3. Set Up the Equations:
Now, we can set up equations based on the lengths given:
- From point A to B:
AB=AD+BD⟹12=x+y(Equation 1)
- From point B to C:
BC=BE+CE⟹8=y+z(Equation 2)
- From point C to A:
AC=CF+AF⟹10=z+x(Equation 3)
4. Solve the Equations:
We now have three equations:
- x+y=12 (Equation 1)
- y+z=8 (Equation 2)
- z+x=10 (Equation 3)
We can solve these equations step by step. Let's first subtract Equation 3 from Equation 2:
(y+z)−(z+x)=8−10⟹y−x=−2⟹x−y=2(Equation 4)
5. Substitute Equation 4 into Equation 1:
Now, we can substitute Equation 4 into Equation 1:
x+y=12⟹(y+2)+y=12⟹2y+2=12⟹2y=10⟹y=5
6. Find x:
Now substitute y=5 back into Equation 1:
x+5=12⟹x=12−5=7
7. Conclusion:
Therefore, the length of segment AD is:
AD=x=7 cm
Final Answer:
AD = 7 cm, which corresponds to option (d).
From point A, we can draw two tangents to the circle, which we will denote as AD and AF. According to the properties of tangents, the lengths of tangents drawn from an external point to a circle are equal. Therefore, we have:
AD=AF
Let's denote AD=AF=x.
Similarly, from point B, we can draw two tangents to the circle, denoting them as BD and BE. We will denote BD=BE=y.
From point C, we can draw two tangents to the circle, denoting them as CE and CF. We will denote CE=CF=z.
Now, we can set up equations based on the lengths given:
- From point A to B:
AB=AD+BD⟹12=x+y(Equation 1)
- From point B to C:
BC=BE+CE⟹8=y+z(Equation 2)
- From point C to A:
AC=CF+AF⟹10=z+x(Equation 3)
We now have three equations:
- x+y=12 (Equation 1)
- y+z=8 (Equation 2)
- z+x=10 (Equation 3)
(y+z)−(z+x)=8−10⟹y−x=−2⟹x−y=2(Equation 4)
Now, we can substitute Equation 4 into Equation 1:
x+y=12⟹(y+2)+y=12⟹2y+2=12⟹2y=10⟹y=5
Now substitute y=5 back into Equation 1:
x+5=12⟹x=12−5=7
Therefore, the length of segment AD is:
AD=x=7 cm
AD = 7 cm, which corresponds to option (d).
Topper's Solved these Questions
Similar Questions
In the adjacent figure, if AB=12cm, BC=8cm and AC=10cm , then AD= (FIGURE) (a) 5cm (b) 4cm (c) 6cm (d) 7cm
View SolutionIn Figure, ABCD is a parallelogram. If AB=12cm,AE=7.5cm,CF=15cm, then AD=

(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
View SolutionIn Fig. 10.97, the sides AB, BC and CA of triangle ABC , touch a circle at P, Q and R respectively. If PA=4cm , BP=3cm and AC=11cm , then length of BC is (FIGURE) (a) 11cm (b) 10cm (c) 14cm (d) 15cm
View SolutionIn Fig. 10.79, RQ is a tangent to the circle with centre O . If SQ=6cm and QR=4cm , then OR= (FIGURE) (a) 8cm (b) 3cm (c) 2.5cm (d) 5cm
View SolutionIn the figure, if DF||BC, AD = 3cm, BD = 4cm and BC = 14cm, then DE equals
(a) 7cm
(b) 6cm
(c) 4cm
(d) 3cm
View SolutionIn Fig. 10.103, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB=x cm , BC=7cm , CR=3cm and AS=5cm , then x= (FIGURE) (a) 10 (b) 9 (c) 8 (d) 7
View SolutionIn Fig. 10.94, if AB=8cm and PE=3cm , then AE= (FIGURE) (a) 11cm (b) 7cm (c) 5cm (d) 3cm
View SolutionABCPQR such that ar(ABC)=4ar(PQR). If BC=12cm , then QR= (a) 9cm (b) 10cm (c) 6cm (d) 8cm
View SolutionIn Fig. 10.90, PR= (FIGURE) (a) 20cm (b) 26cm (c) 24cm (d) 28cm
View SolutionIn Figure, if AC is bisector fo ∠BAD such that AB=3 cm and AC=5 cm, then CD= 2 cm (b) 3 cm (c) 4 cm (d) 5 cm
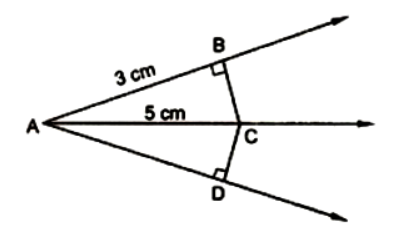
View Solution
