Construct a ABC in which AB=4cm , BC=5cm and AC=6cm . Now, construct a triangle similar to ABC such that each of its sides is two-third of the corresponding sides of ABC . Also, prove your assertion.
To construct triangle ABC with sides AB = 4 cm, BC = 5 cm, and AC = 6 cm, and then construct a similar triangle with sides that are two-thirds of the corresponding sides of triangle ABC, follow these steps:
1. Draw Base AB:
- Using a ruler, draw a line segment AB of length 4 cm. Label the endpoints as A and B.
Hint: Use the ruler to measure exactly 4 cm and mark the points clearly.
2. Construct an Arc for BC:
- With a compass, set the width to 5 cm (the length of BC). Place the compass point on B and draw an arc above the line segment AB.
Hint: Make sure the compass is not moved while drawing the arc to maintain the correct length.
3. Construct an Arc for AC:
- Now, set the compass to 6 cm (the length of AC). Place the compass point on A and draw another arc that intersects with the first arc drawn from point B.
Hint: Ensure the compass remains at 6 cm while drawing the arc from A.
4. Label Intersection Point:
- Let the intersection of the two arcs be point C. Now you have points A, B, and C.
Hint: Mark point C clearly where the two arcs intersect.
5. Join Points to Form Triangle ABC:
- Use a ruler to draw line segments AC and BC to complete triangle ABC.
Hint: Ensure the lines are straight and connect the points accurately.
6. Extend Line AB:
- Extend line AB in both directions to prepare for constructing the similar triangle.
Hint: Use a ruler to extend the line straight without bending.
7. Constructing the Similar Triangle:
- To find the points for the similar triangle, we need to find points A1, B1, and C1 such that the sides are two-thirds of the original triangle.
- From point A, make an angle with the extended line AB using a compass.
Hint: Use a protractor to ensure the angle is acute.
8. Marking Points for Similar Triangle:
- From point A, mark three equal divisions along the angle you created. Label them A1, A2, and A3 where A1 is closest to A.
Hint: Use the compass to ensure equal spacing for the divisions.
9. Join A2 to B:
- Draw a line from A2 to point B.
Hint: Ensure the line is straight and connects both points clearly.
10. Constructing Parallel Lines:
- Using the compass, measure the distance A2B and mark the same distance from A3 to create point B1.
- Repeat this process to find point C1 by measuring the distance from B to C and marking it from B1.
Hint: Keep the compass width the same while marking points.
11. Finalizing the Similar Triangle:
- Join points A3, B1, and C1 to complete triangle A1B1C1.
Hint: Make sure the lines are drawn straight and connect the points accurately.
12. Proving Similarity:
- To prove that triangle A1B1C1 is similar to triangle ABC, show that the ratio of corresponding sides is 2:3.
- Since A1B1 is parallel to AB, angles A1B1C1 and ABC are equal. Similarly, angles A1C1B1 and ACB are equal.
Hint: Use the properties of parallel lines and angles to justify the similarity.
Conclusion:
- By following these steps, you have constructed triangle ABC and a similar triangle A1B1C1, where each side of A1B1C1 is two-thirds the length of the corresponding side of triangle ABC. The triangles are similar due to the Angle-Angle (AA) criterion for similarity.
- Using a ruler, draw a line segment AB of length 4 cm. Label the endpoints as A and B.
- With a compass, set the width to 5 cm (the length of BC). Place the compass point on B and draw an arc above the line segment AB.
- Now, set the compass to 6 cm (the length of AC). Place the compass point on A and draw another arc that intersects with the first arc drawn from point B.
- Let the intersection of the two arcs be point C. Now you have points A, B, and C.
- Use a ruler to draw line segments AC and BC to complete triangle ABC.
- Extend line AB in both directions to prepare for constructing the similar triangle.
- To find the points for the similar triangle, we need to find points A1, B1, and C1 such that the sides are two-thirds of the original triangle.
- From point A, make an angle with the extended line AB using a compass.
- From point A, mark three equal divisions along the angle you created. Label them A1, A2, and A3 where A1 is closest to A.
- Draw a line from A2 to point B.
- Using the compass, measure the distance A2B and mark the same distance from A3 to create point B1.
- Repeat this process to find point C1 by measuring the distance from B to C and marking it from B1.
- Join points A3, B1, and C1 to complete triangle A1B1C1.
- To prove that triangle A1B1C1 is similar to triangle ABC, show that the ratio of corresponding sides is 2:3.
- Since A1B1 is parallel to AB, angles A1B1C1 and ABC are equal. Similarly, angles A1C1B1 and ACB are equal.
- By following these steps, you have constructed triangle ABC and a similar triangle A1B1C1, where each side of A1B1C1 is two-thirds the length of the corresponding side of triangle ABC. The triangles are similar due to the Angle-Angle (AA) criterion for similarity.
Topper's Solved these Questions
Similar Questions
Draw ΔABC with sides = 6 cm, 8 cm and 9 cm and then construct a triangle similar to ΔA'B'C whose sides are 35 or the corresponding sides of ΔABC.
View SolutionIf A, B, C are the angles of a triangle and tanA=1,tanB=2, prove that tanC=3. If a, b, c are the corresponding sides, then prove that a√5=b2√2=c3
View Solution
Knowledge Check
If sides of triangle ABC are a, b, and c such that 2b=a+c, then
Abc>23Bbc>13Cbc<2Dbc<32
AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle
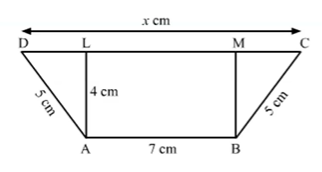
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
View SolutionIf triangle ABC is similar to triangle DEF such that BC=3CM,EF=4cm and area of triangle ABC=54cm2 . Determine the area of triangle DEF.
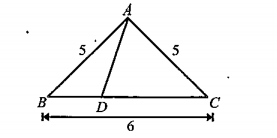
View SolutionFigure shows triangle ABC such that AB=AC=5,BC=6.P∮DisonB Csuchtˆ(B D)/(D C)=1/2,then□of≤n>hofsA D is
View SolutionIn a ABC , AD is the bisector of ∠BAC . If AB=8cm , BD=6cm and DC=3cm . Find AC 4cm (b) 6cm (c) 3cm (d) 8cm
View SolutionIn a ABC , AD is the bisector of ∠BAC . If AB=6cm , AC=5cm and BD=3cm , then DC= 11.3cm (b) 2.5cm (c) 3:5cm (d) None of these
View SolutionABC is a triangle and PQ is a straight line meeting AB in P and AC in Q . If AP=1cm , PB=3cm , AQ=1.5cm , QC=4.5m , prove that area of APQ is one-sixteenth of the area of ABC .
View Solution
