In the adjoining figure, A and B are the centres of two circles. If CB=17cm, EB=15cm, then find the length of common chord.
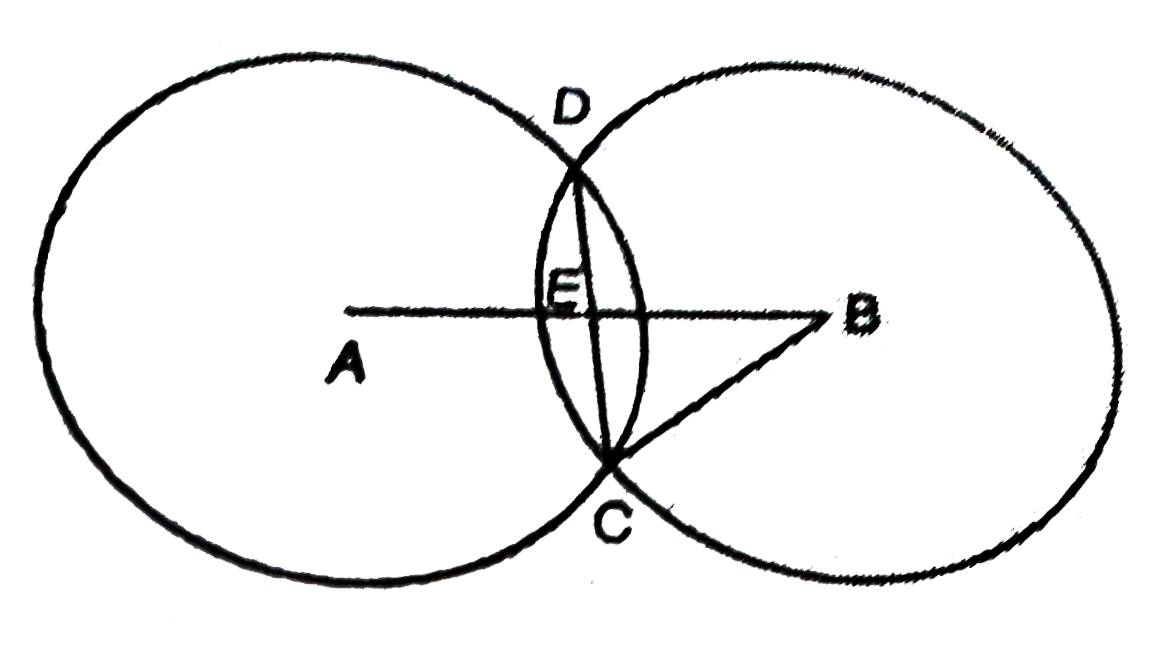
The linc segment joining the centres of the circles bisect the common chord at right angle
∴∠BEC=90∘
In ΔBEC,
BE2+EC2=BC2 (by Pythagoras theoram)
⇒EC2=BC2−BE2=172−152=289−225=64
⇒EC=√64=8cm
Now, CD=2EC (Property 1)
=2×8=16cm
∴ Length of common chord= 16 cm .
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
The radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
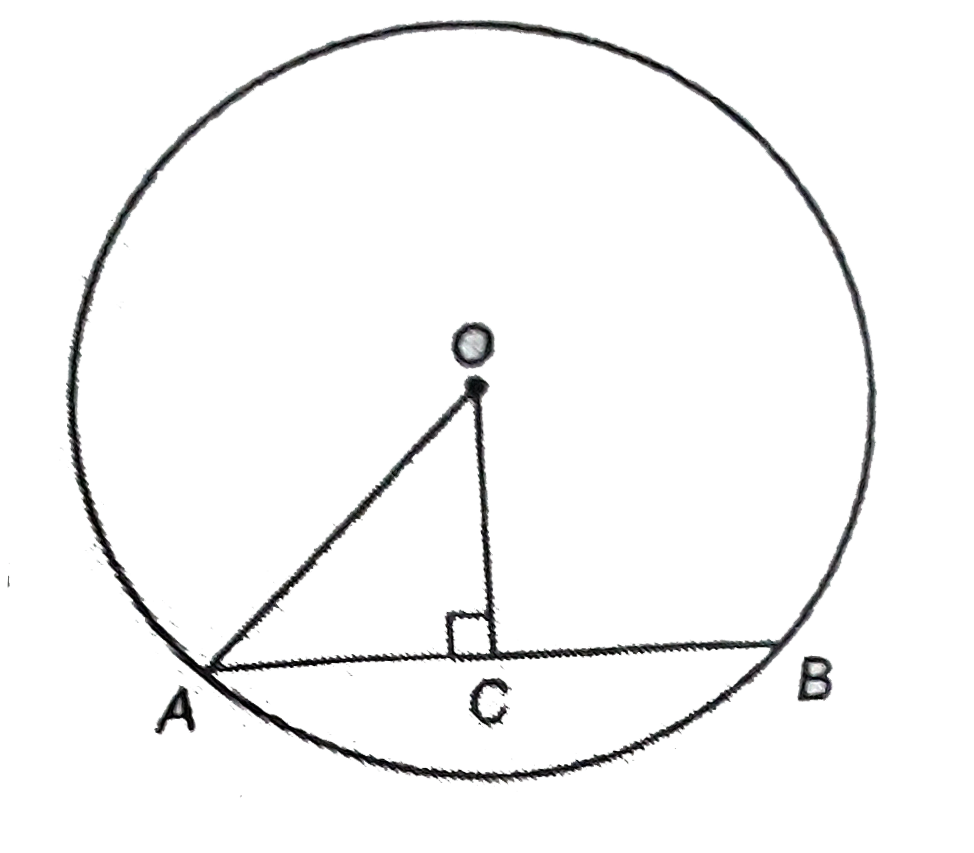
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
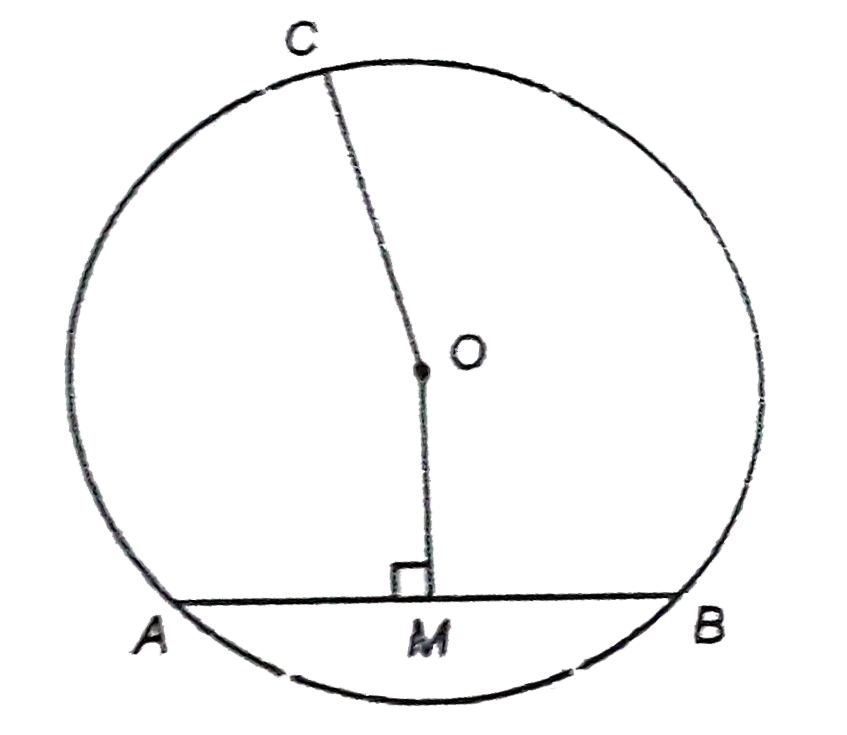
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
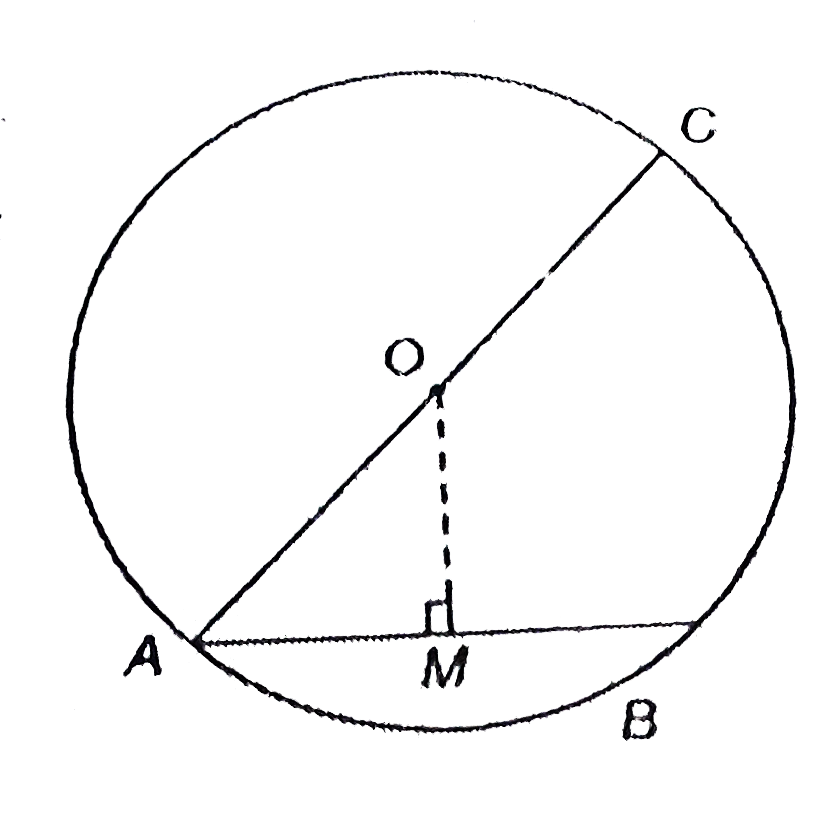
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
View Solution
Knowledge Check
In the adjoining figure O is the centre of the circle . If chord AB=2 cm radius OA=2 cm, then find the value of ∠ACB.
 A=60∘B=45∘C=30∘D=50∘
A=60∘B=45∘C=30∘D=50∘In the given figure, O is the centre of the circle. Radius of the circle is 17 cm. lf OC=8cm, then the length of the chord AB is :
 A35 cmB30 cmC15 cmD18 cm
A35 cmB30 cmC15 cmD18 cmTwo circles of equal radii intersect each other such that one circle will pass through the centre of the other circle. The distance between the centre of two circles is equal to 6 cm. Find the length (in cm) of common chord.
A√3B2√3C3√3D6√3
In the adjoining figure ,PT is tangent to a circle with centre O . if OP= 25 cm and radius of circle is 7cm , then find the length of the tangent PT .
View SolutionThe distance between centres of two circle with radius 15 cm and 20 cm is 25 cm. Then find out the length of the common chord of the circles.
View SolutionTwo circles with equal radius passes through the centres of each other. If the radius of each circle is 5 cm then find the length of common chord.
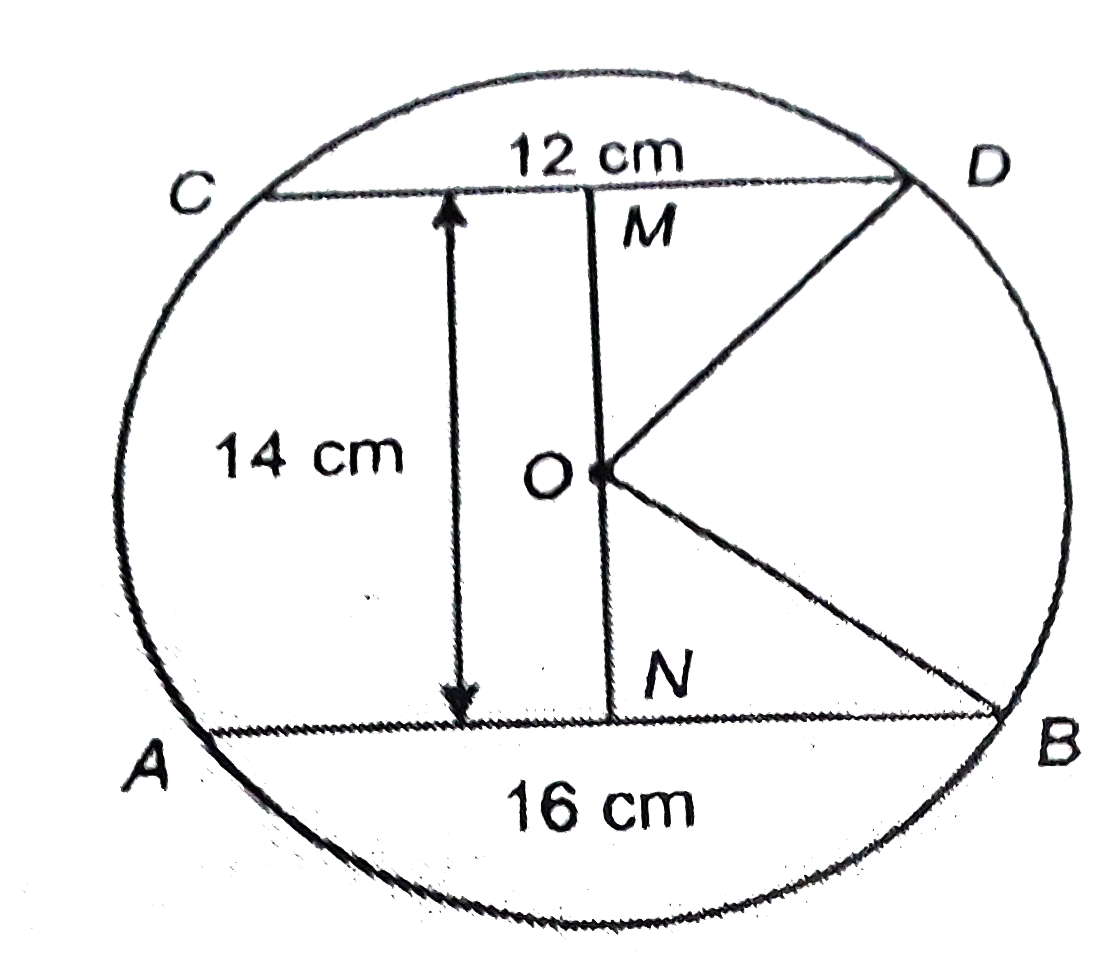
View SolutionIn the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
View SolutionTwo circles with centres A and B of radii 3 cm and 4 cm respectively intersect at two points C and D, such that AC and BC are tangents to the two circle. Find the length of the common chord CD.
View Solution
