Two circles with equal radius passes through the centres of each other. If the radius of each circle is 5 cm then find the length of common chord.
5
5√3
10√3
5√32
To find the length of the common chord between two circles that pass through each other's centers, we can follow these steps:
Step 1: Understand the Configuration
We have two circles with equal radius r=5 cm, and the distance between their centers OO′ is equal to the radius, which is also 5 cm.
Step 2: Identify Key Points
Let:
- O be the center of the first circle.
- O′ be the center of the second circle.
- A and B be the points where the common chord intersects the circles.
- M be the midpoint of the common chord AB.
Step 3: Calculate the Distance OO′
Since both circles pass through each other's centers, we have:
OO′=r=5 cm
Step 4: Find the Length OM
The distance from the center O to the midpoint M of the common chord can be calculated using the right triangle OAM. Here, OA is the radius of the circle, and OM is the distance from the center to the midpoint of the chord.
Using the property of the triangle:
OM=OO′2=52=2.5 cm
Step 5: Apply the Pythagorean Theorem
In triangle OAM:
OA2=OM2+AM2
Substituting the known values:
52=(52)2+AM2
Calculating the squares:
25=(254)+AM2
Rearranging gives:
AM2=25−254=1004−254=754
Taking the square root:
AM=√754=√752=5√32 cm
Step 6: Calculate the Length of the Common Chord AB
The length of the common chord AB is twice the length of AM:
AB=2×AM=2×5√32=5√3 cm
Final Answer
Thus, the length of the common chord is:
5√3 cm
We have two circles with equal radius r=5 cm, and the distance between their centers OO′ is equal to the radius, which is also 5 cm.
Let:
- O be the center of the first circle.
- O′ be the center of the second circle.
- A and B be the points where the common chord intersects the circles.
- M be the midpoint of the common chord AB.
Since both circles pass through each other's centers, we have:
OO′=r=5 cm
The distance from the center O to the midpoint M of the common chord can be calculated using the right triangle OAM. Here, OA is the radius of the circle, and OM is the distance from the center to the midpoint of the chord.
OM=OO′2=52=2.5 cm
In triangle OAM:
OA2=OM2+AM2
Substituting the known values:
52=(52)2+AM2
Calculating the squares:
25=(254)+AM2
Rearranging gives:
AM2=25−254=1004−254=754
Taking the square root:
AM=√754=√752=5√32 cm
The length of the common chord AB is twice the length of AM:
AB=2×AM=2×5√32=5√3 cm
Thus, the length of the common chord is:
5√3 cm
Topper's Solved these Questions
Similar Questions
The radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
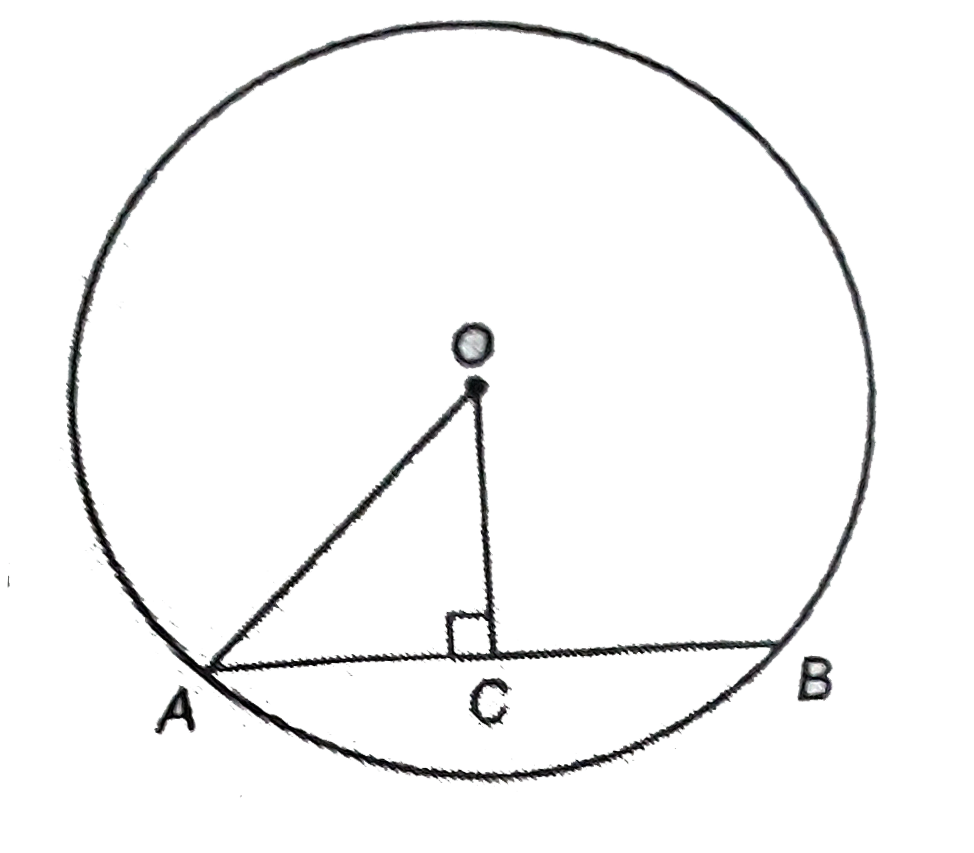
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
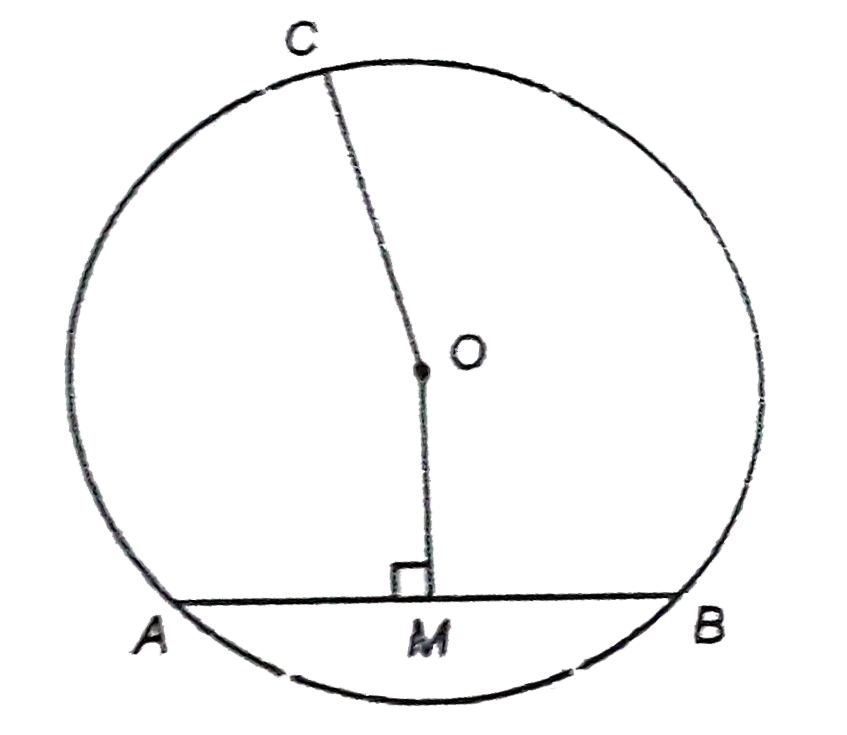
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
View SolutionTwo equal circles intersect such that each passes through the centre of the other. If the length of the common chord of the circles is 10√3 cm, then what is the diameter of the circle?
View Solution
Knowledge Check
Two equal circles pass through each other centre. If the radius of each circle is 5 cm, what is the length of the common chord?
A5B5√3C10√3D5√32it two circles, A, B of equal radii pass through the centres of each other, then what is the ratio of the length of the smaller arc to the circumference of the circle A but off by the circle
A12B14C13D23Each of the two circles of same radius a passes through the centre of the other. If the circles cut each other at the points A, B and 0,0' be their centres, then area of the quadrilateral AOBO' is
A14a2B12a2C√32a2Da2
Each of the two circles of same radius 'a' passes through the centre of the other, If the circles cut each other at the points A and Band O, O'be their centres, area of the quadrilateral AOBO' is :
View SolutionTwo circles with same radius r intersect each other and one passes through the centre of the other. Then the length of the common chord is
View SolutionTwo circles with same radius r intersect each other and one passes through the centre of the other. Then the length of the common chord is
View SolutionTwo circles touch each other externally. The distance between their centres is 7 cm. If the radius of one circle is 4 cm, then the radius of the other circle is
View SolutionTwo circles touch each other externally. The distance between their centres is 7 cm. If the radius of one circle is 4 cm, then the radius of the other circle is
View Solution