In the adjoining figure, A and B are the centres of two circles. If CB=17cm, EB=15cm, then find the length of common chord.
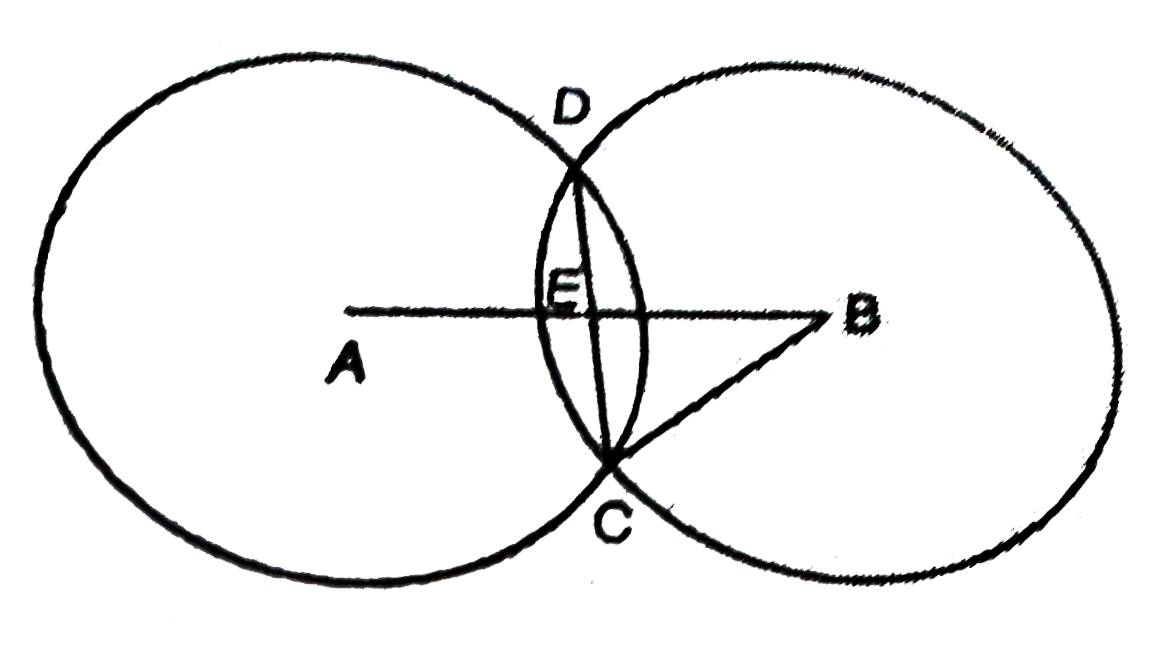
The linc segment joining the centres of the circles bisect the common chord at right angle
∴∠BEC=90∘
In ΔBEC,
BE2+EC2=BC2 (by Pythagoras theoram)
⇒EC2=BC2−BE2=172−152=289−225=64
⇒EC=√64=8cm
Now, CD=2EC (Property 1)
=2×8=16cm
∴ Length of common chord= 16 cm .
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a22videos
CIRCLE
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b19videos
CIRCLE
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
Similar Questions
In the adjoining figure O is the centre of the circle . If chord AB=2 cm radius OA=2 cm, then find the value of ∠ACB.
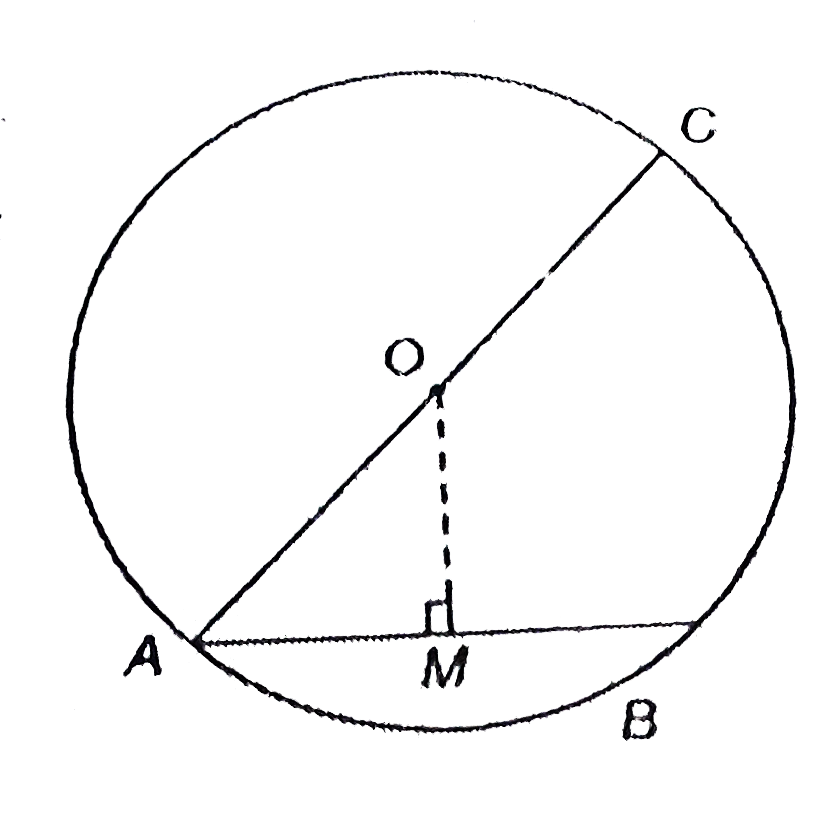
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
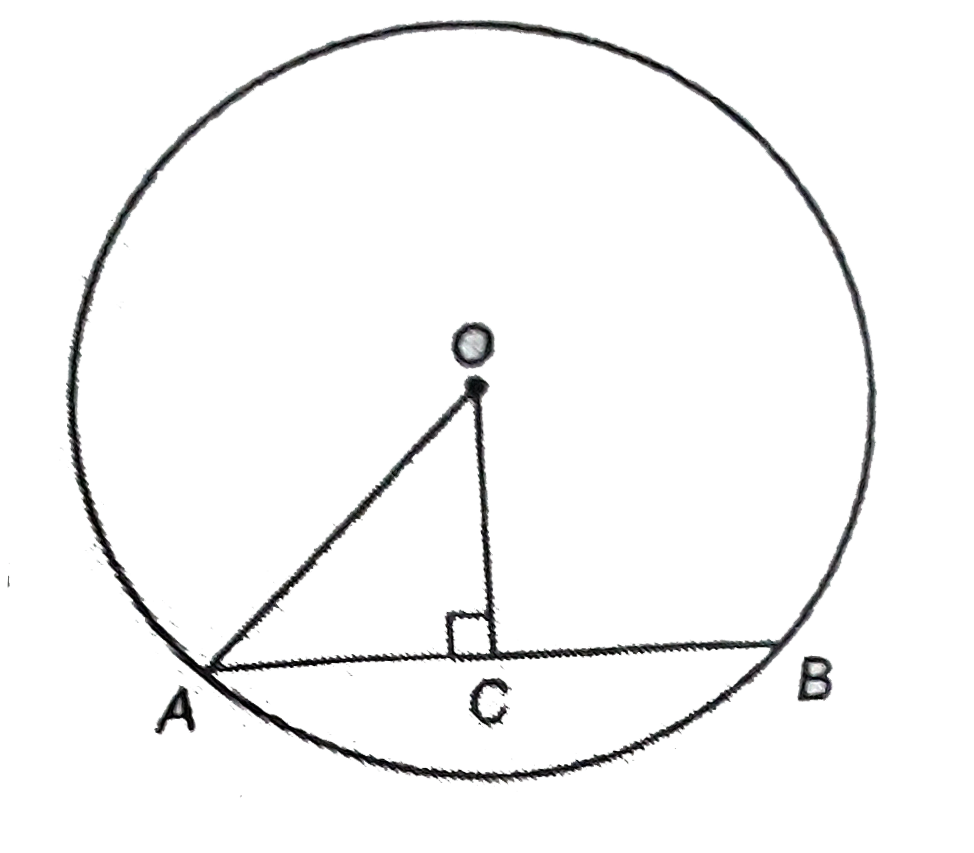
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.
View SolutionIn the adjoining figure O is the centre of circle and c is the mid point. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠BOD=50∘, then find ∠BCD.
(ii) In the adjoining figure,O is the centre of the circle. If ∠ABC=20∘, then find ∠AOC.
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.
View SolutionIn the adjoining figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90∘. Find the area of the shaded region.
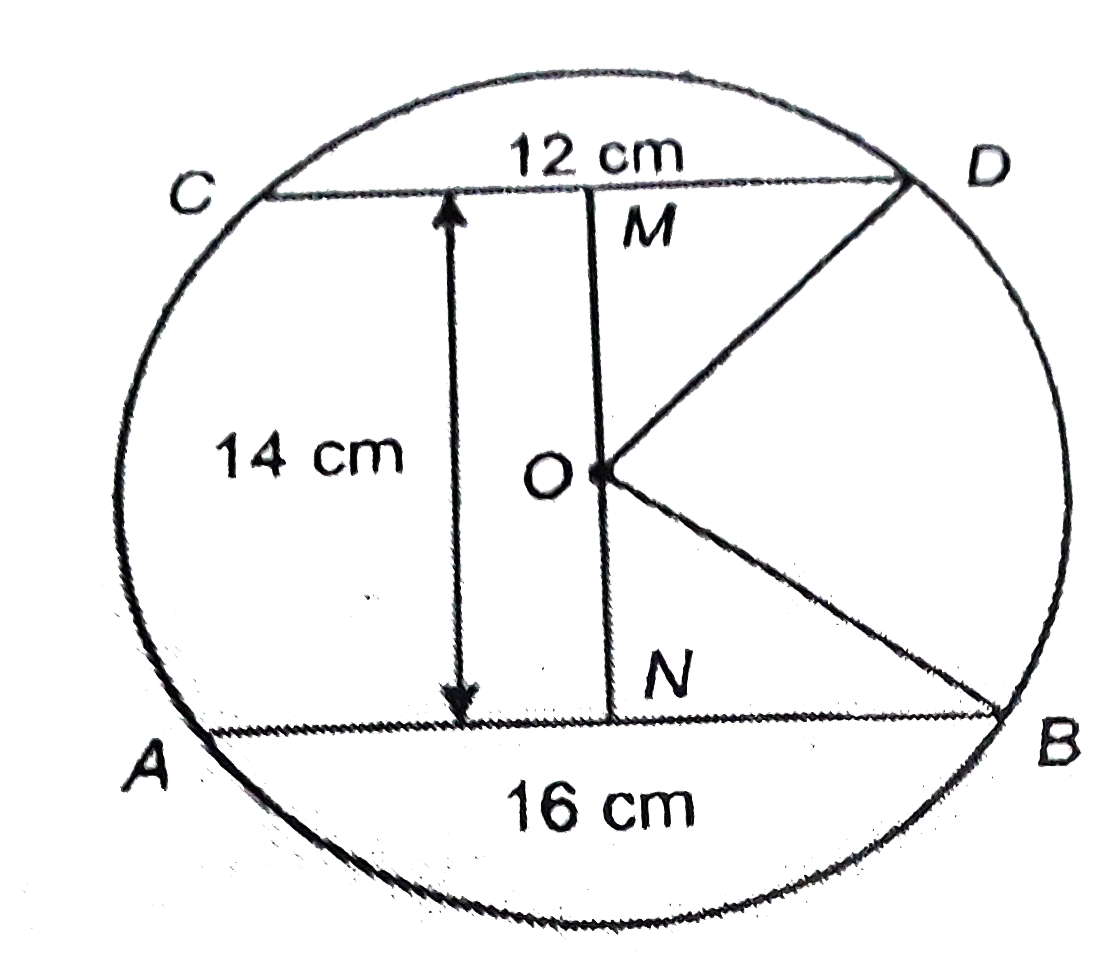
View SolutionIn the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
View SolutionThe radius of a circle is 15cm. Find the length of its longest chord.
View SolutionIn the adjoining figure, two circles cut at A and B. P and Q are the centres of the circles. If ∠APB=90∘and∠AQB=60∘, then find the area of the shaded portion if AP = 4 cm. (Use =√3=1.73)
View Solution