In the adjoining figure, ABC is a triangle in which side BC has been produced to D. If ∠BAC=x∘,∠ABC=(4a)∘,and∠ACD=(5a)∘, find the values of a a and x.

The correct Answer is:30
Step by step video, text & image solution for In the adjoining figure, ABC is a triangle in which side BC has been produced to D. If /_BAC=x^(@), /_ABC=(4a)^(@),"and" /_ACD=(5a)^(@), find the values of a a and x. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Exercise 18A
23 Videos
- PROPERTIES OF TRIANGLESBOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Exercise 18B
10 Videos
- PROPERTIES OF TRIANGLESBOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Exercise 18B
10 Videos
- PROFIT AND LOSS BOOK - ICSECHAPTER - PROFIT AND LOSS EXERCISE - EXERCISE 10
18 Videos
- RATIO AND PROPORTIONBOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - Challenge
1 Videos
Similar Questions
Knowledge Check
In the figure, triangle ABC and ABD are right triangle , what is the value of x?
 A20B30C50D70
A20B30C50D70
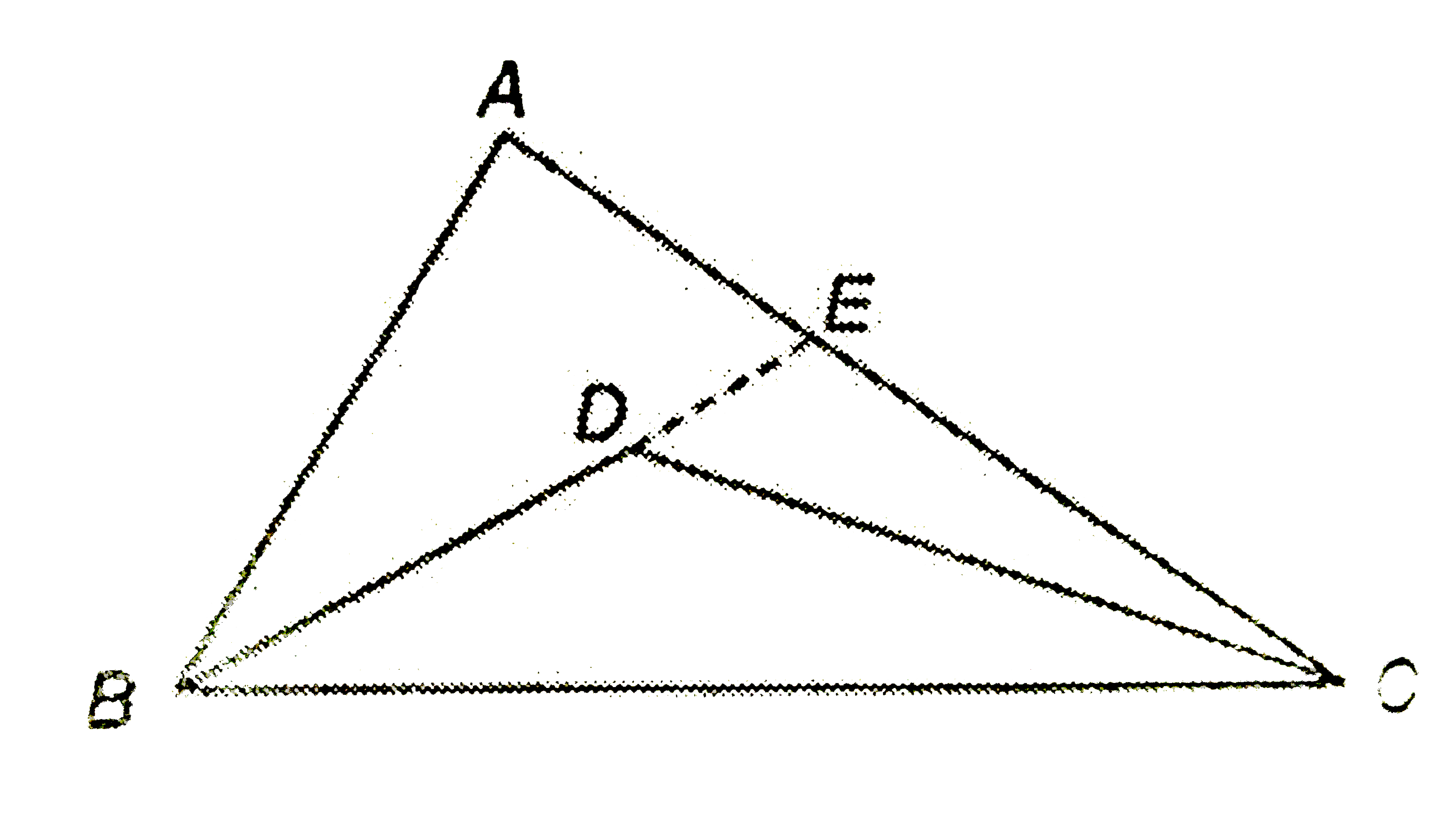
In the adjoining figure, ΔABC is an isosceles triangle. Find the value of ∠BDC and ∠BEC.
View SolutionIn the adjoining figure, ∠ABC=95∘ and ∠DAC=35∘, then find the value of ∠ACD.

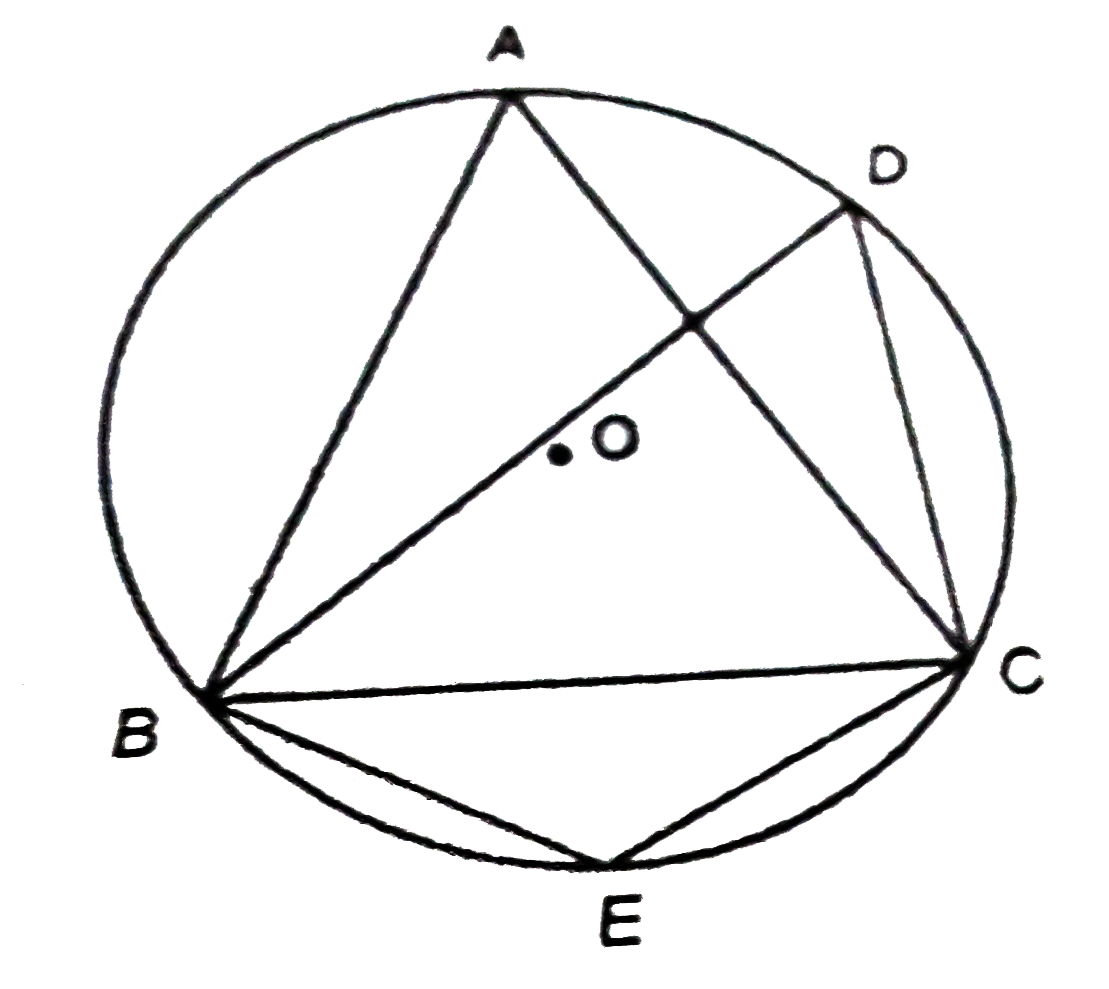
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral.If side BC is produced upto point E and ∠DAB=95∘, then find the value of ∠DCE.

View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.

If BD = 18 cm and CD = 8 cm, find AD.
View SolutionABC is a triangle and G (4, 3) is the centroid of the triangle. If A = (1, 3), B = (4, b) and C = (a, 1), find 'a' and 'b'.
Find the length of side BC.
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.

If BD = 3.6 cm and CD = 6.4 cm, find the length of AD.
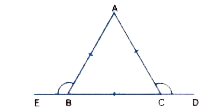
View SolutionIn the given figure, ΔABC is an equilateral triangle whose side BC has been produced in both the directions to D and E respectively. Prove that ∠ACD=∠ABE.
View Solution