The sides AB and AC of ABC have been produced to D and E reapectively. The bisectors of ∠CBD and ∠BCE meet at O. If ∠A=50∘, find ∠BOC.
50∘
55∘
60∘
65∘
The correct Answer is:D
To find the angle ∠BOC in triangle ABC where ∠A=50∘, we can follow these steps:
1. Draw the Triangle: Start by sketching triangle ABC with A at the top, B on the left, and C on the right. Extend side AB to point D and side AC to point E.
2. Label the Angles: Mark ∠A=50∘. Let ∠B=P and ∠C=Q.
3. Use the Angle Sum Property: According to the angle sum property of triangles, we have:
∠A+∠B+∠C=180∘
Substituting the known value:
50∘+P+Q=180∘
This simplifies to:
P+Q=130∘(Equation 1)
4. Identify Exterior Angles: The angle ∠CBD is an exterior angle for triangle ABC:
∠CBD=∠A+∠C=50∘+Q
Since ∠CBD is bisected by line BO, we have:
∠CBD=2xwhere x=the angle on either side of the bisector
Thus:
2x=50∘+Q⇒x=12(50∘+Q)
5. Similarly for ∠BCE: The angle ∠BCE is also an exterior angle:
∠BCE=∠A+∠B=50∘+P
This angle is bisected by line CO:
2y=50∘+P⇒y=12(50∘+P)
6. Find ∠BOC: In triangle BOC, we have:
∠BOC+∠OBC+∠BCO=180∘
Substituting OBC=x and BCO=y:
∠BOC+x+y=180∘
Therefore:
∠BOC=180∘−(x+y)
7. Substitute Values of x and y:
∠BOC=180∘−(12(50∘+Q)+12(50∘+P))
Combining the terms inside the parentheses:
∠BOC=180∘−12(100∘+P+Q)
From Equation 1, we know P+Q=130∘:
∠BOC=180∘−12(100∘+130∘)
Simplifying gives:
∠BOC=180∘−12(230∘)=180∘−115∘=65∘
Final Answer:
∠BOC=65∘
∠A+∠B+∠C=180∘
Substituting the known value:
50∘+P+Q=180∘
This simplifies to:
P+Q=130∘(Equation 1)
∠CBD=∠A+∠C=50∘+Q
Since ∠CBD is bisected by line BO, we have:
∠CBD=2xwhere x=the angle on either side of the bisector
Thus:
2x=50∘+Q⇒x=12(50∘+Q)
∠BCE=∠A+∠B=50∘+P
This angle is bisected by line CO:
2y=50∘+P⇒y=12(50∘+P)
∠BOC+∠OBC+∠BCO=180∘
Substituting OBC=x and BCO=y:
∠BOC+x+y=180∘
Therefore:
∠BOC=180∘−(x+y)
∠BOC=180∘−(12(50∘+Q)+12(50∘+P))
Combining the terms inside the parentheses:
∠BOC=180∘−12(100∘+P+Q)
From Equation 1, we know P+Q=130∘:
∠BOC=180∘−12(100∘+130∘)
Simplifying gives:
∠BOC=180∘−12(230∘)=180∘−115∘=65∘
∠BOC=65∘
Topper's Solved these Questions
- BOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Exercise 18A23videos
PROPERTIES OF TRIANGLES
- BOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Exercise 18B10videos
PROPERTIES OF TRIANGLES
- BOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Exercise 18B10videos
PROPERTIES OF TRIANGLES
- BOOK - ICSECHAPTER - PROFIT AND LOSS EXERCISE - EXERCISE 1018videos
PROFIT AND LOSS
- BOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - Challenge1videos
RATIO AND PROPORTION
Similar Questions
In ΔABC, the angle bisectors of ∠Band∠C meet at O. If ∠A=70∘, find ∠BCO=12∠C.
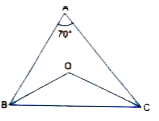 View Solution
View SolutionThe sides AB and AC of a ABC are produced to P and Q respectively. If the bisectors of ∠PBC AND ∠QCB intersect at O, then ∠boc=900−12∠A GIVEN : A ABC in which sides AB and AC are produced to P and Q respectively. The bisectors of ∠PBC and ∠QCB intersect at O.
View SolutionIn Fig. 6.38, the sides AB and AC of ABC are produced to points E and D respectively. If bisectors BO and CO of CBE and BCD respectively meet at point O, then prove that ∠BOC=90∘−12∠BAC.
View SolutionIn Figure, the sides BC, CA and AB of a ABC have been produced to D, E and F respectively. If ∠ACD=1050 and ∠EAF=450, find all the angles of the ABC
View SolutionIn Figure, side BC of ABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC=680, find ∠BEC
View SolutionIn ABC, ∠A=500 and BC is produced to a point D. The bisectors of ∠ABC and ∠ACD meet at E. find ∠E.
View SolutionThe sides AB and AC of a triangle ABC are produced, and the bisectors of the external angles at B and C meet at P. Prove that if AB>AC, then PC>PB.
View SolutionThe sides BC of ΔABC is produced to a point D . The bisector of ∠A meets side BC in L . If ∠ABC=300 and ∠ACD=1150, find ∠ALC
View SolutionIn a parallelogram ABCD, the bisectors of ∠A and ∠B meet at O. Find ∠AOB.
View SolutionIn ABC, ∠A=600, ∠B=800 and the bisectors of ∠B and ∠C meet at O . Find : (i) ∠C (ii) ∠BOC.
View Solution

