In the adjoining figure AB∣∣CD and EF is a transversal cutting them at G and H respactively. if GL and HM are the bisectors of the corresponding angels EGB and EHD respectively show that GL||HM.
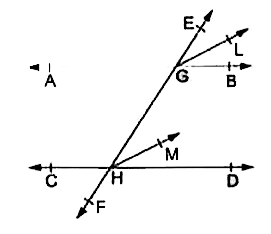
The correct Answer is:GL∣∣HM
Step by step video, text & image solution for In the adjoining figure AB||CD and EF is a transversal cutting them at G and H respactively. if GL and HM are the bisectors of the corresponding angels EGB and EHD respectively show that GL||HM. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF PARALLEL LINE BOOK - RS AGGARWALCHAPTER - PROPERTIES OF PARALLEL LINE EXERCISE - EXERCISE 14
15 Videos
- PROFIT AND LOSSBOOK - RS AGGARWALCHAPTER - PROFIT AND LOSSEXERCISE - Test paper
9 Videos
- PROPERTIES OF TRIANGLESBOOK - RS AGGARWALCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE 15-D
18 Videos
Similar Questions
In the given figure, AB∣∣CD and a transversal t cuts them at E and F respectively. If EP and FQ are the bisectors of ∠AEF and ∠EFD respectively, prove that EP∣∣FQ.

View SolutionIn the given figure, AB∣∣CD and a transversal t cuts them at E and F respectively. If EG and FG are this bisectors of ∠BEF and ∠EFD respectivelym prove that ∠EGF=90∘.

View Solution
Knowledge Check
Two parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
A180∘B60∘C90∘DNone of theseTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
A180∘B60∘C90∘Dnone of theseTwo parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘
In the following figure AB||CD,QM and RN are bisectors of corresponding angles PQB and QRD respectively. Show that QM ||RN

View SolutionIn the figure given below AB∣∣CD.EF is the transversal, intersections, ABandCD at 'G'and'H' respectively. Find the value of 'x'?
View SolutionIn the following figure, AB||CD, QM and RN are bisectors of alternate angles AQR and QRD respectively. Show that QM||RN.
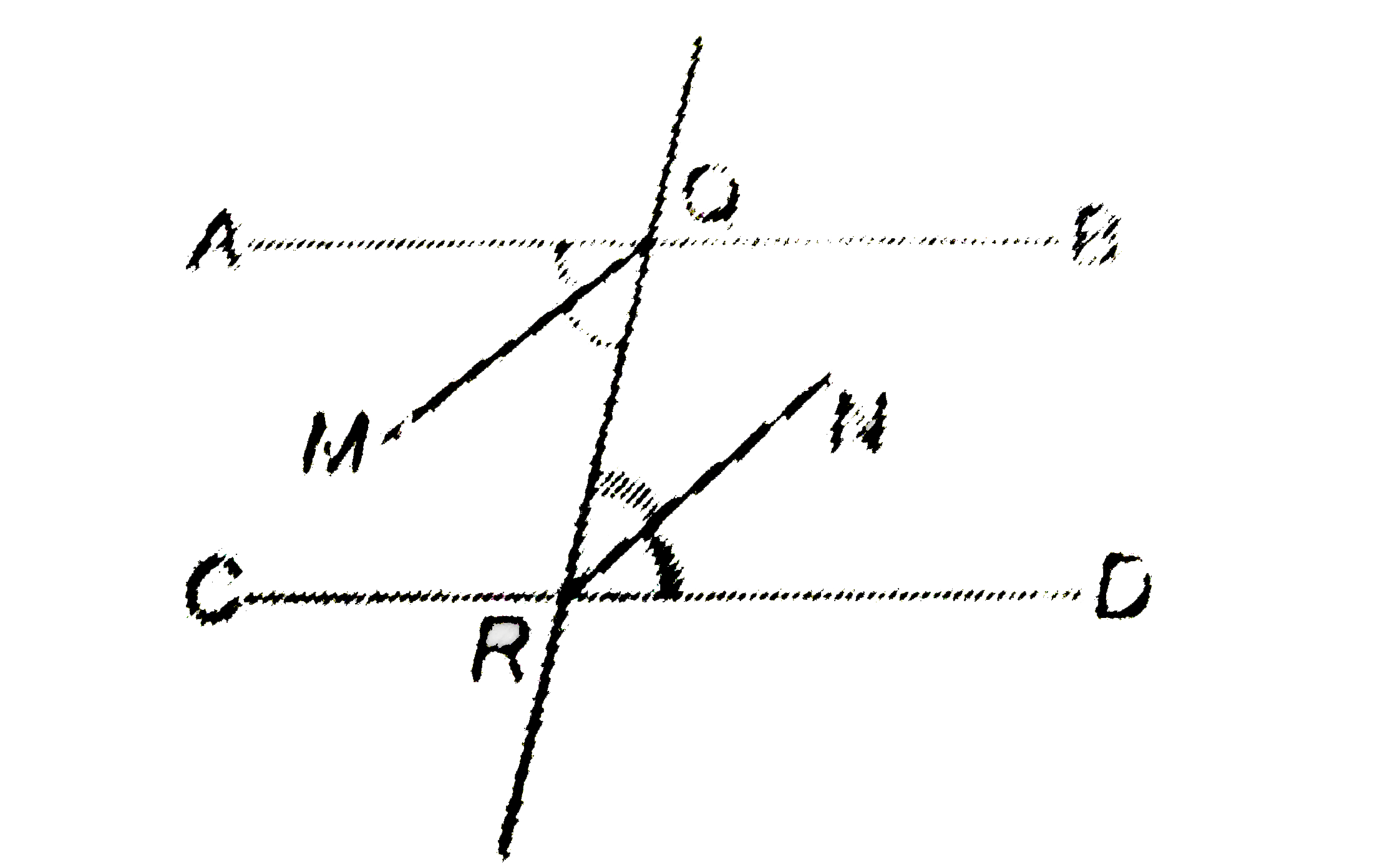
View SolutionTwo parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :
View SolutionIn the figure AB || CD and PQ,QR intersects AB and CD both at E,F, and G,H respectively. If ∠PQR =x, then find the value of x (in degrees).
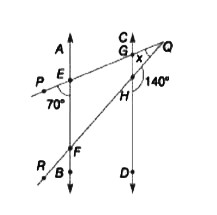
View Solution
