Doubtnut Promotions Sticky

In the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP
In the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find : (i) angleAPD (ii) anglePDC (iii) angleDPC (iv) Prove that DP = CP

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:(i) 15∘ (ii) 75∘ (iii) 30∘

|
Answer

Step by step video, text & image solution for In the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find : (i) angleAPD (ii) anglePDC (iii) angleDPC (iv) Prove that DP = CP by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023
Class 9MATHSTRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

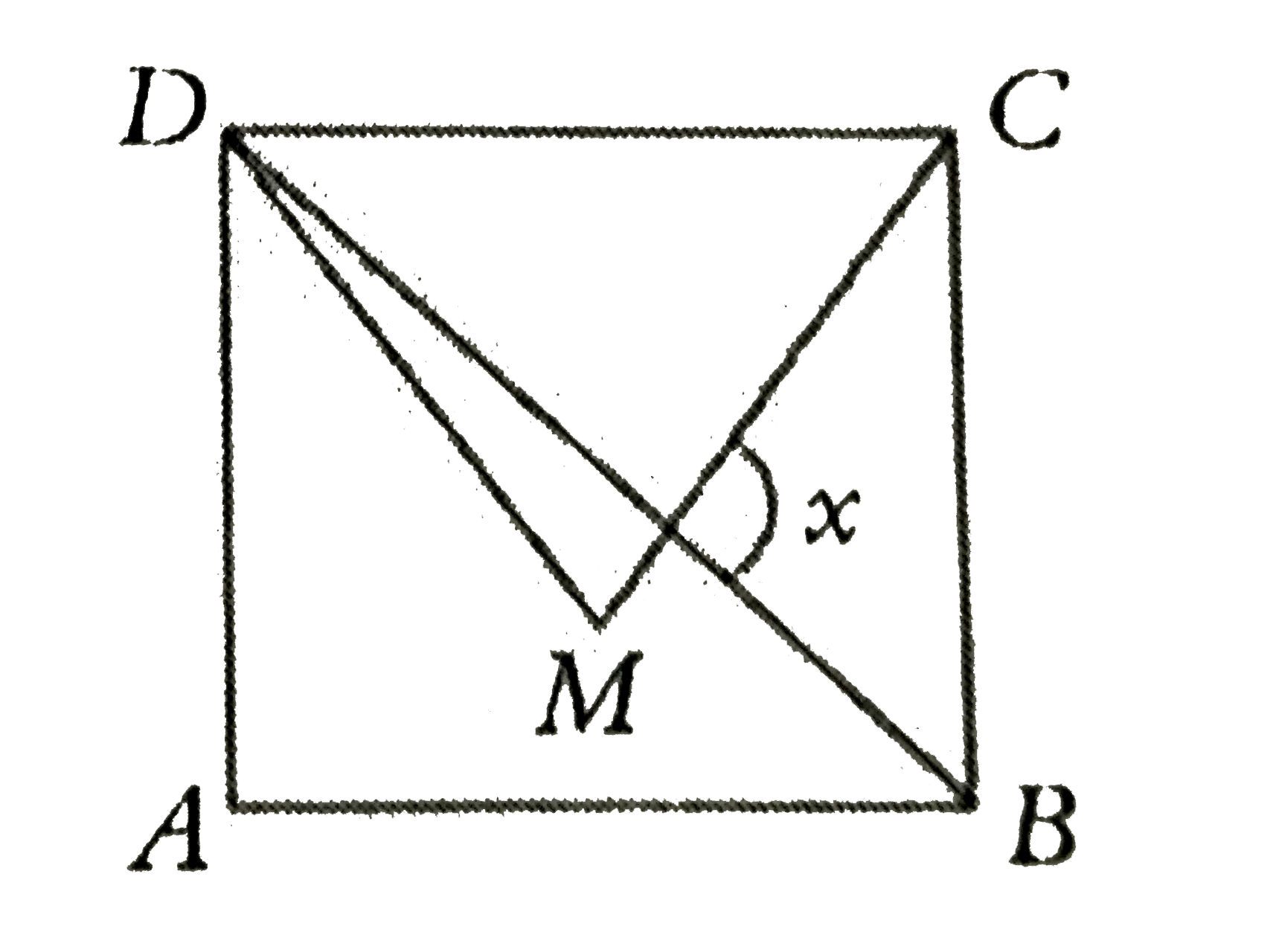
    In the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
    ocr_image

    A75∘
    B90∘
    C105∘
    D60∘
  • Question 2 - Select One

    In the adjoining figure, ABCD is a rhombus and ABE is an equilateral triangle. If ∠BCD=70∘, find
    (a)∠ADE (b)∠BDE (c)∠BED
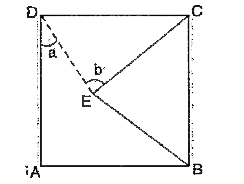
    ocr_image

    A(a)20∘(b)40∘(c)30∘
    B(a)25∘(b)30∘(c)35∘
    C(a)30∘(b)45∘(c)15∘
    D(a)40∘(b)30∘(c)20∘
  • Question 3 - Select One

    ABCD is a square and BCE is an equilateral triangle. Find the value of a,b and reflex ∠BED.
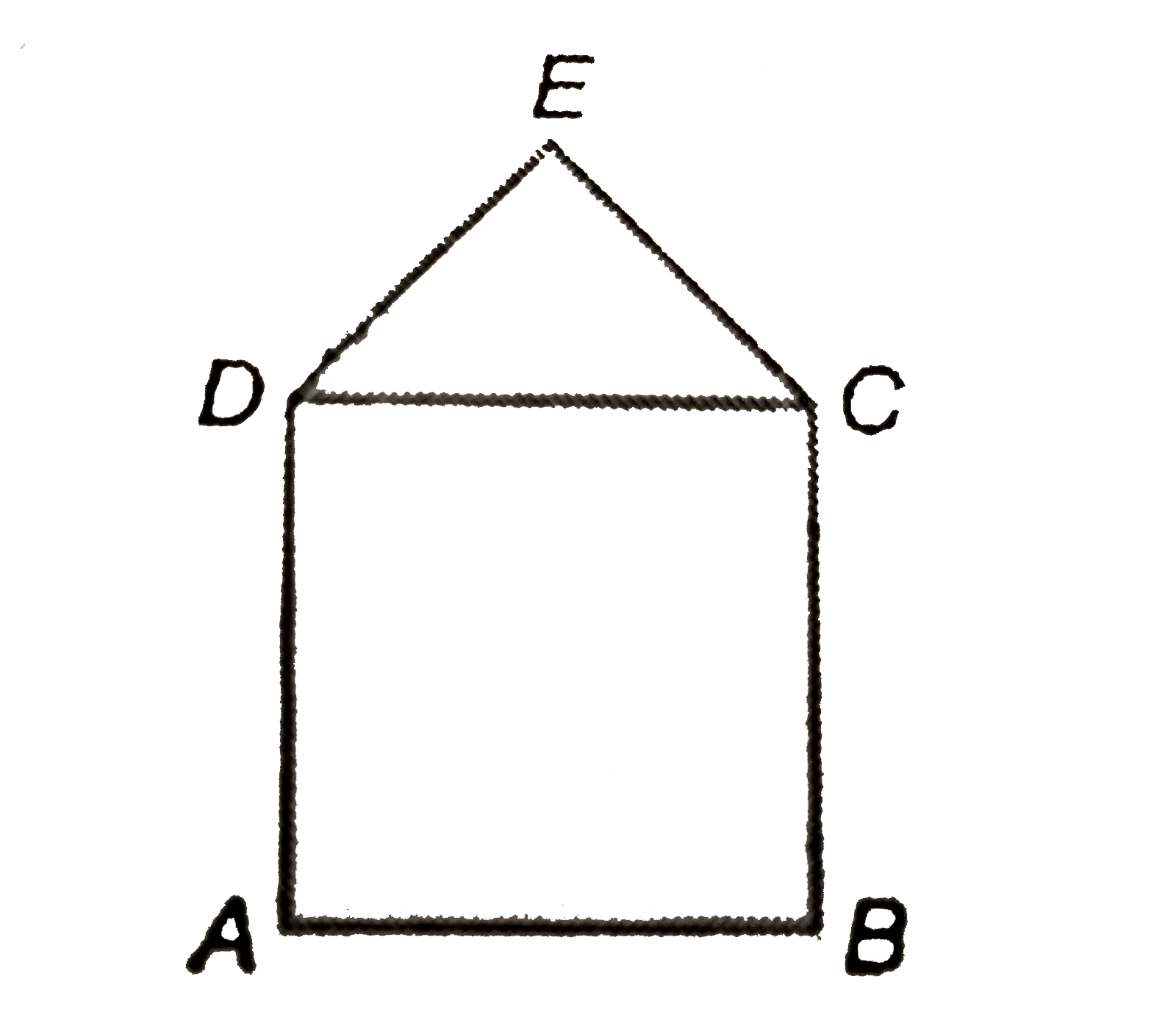
    ocr_image

    A20°, 70°, 230°
    B18°, 72°, 210°
    C15°, 75°, 225°
    D25°, 65°, 210°