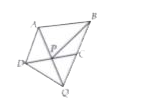
In the adjoining figure, ABCD is a paralogram. The side AB is produced

ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
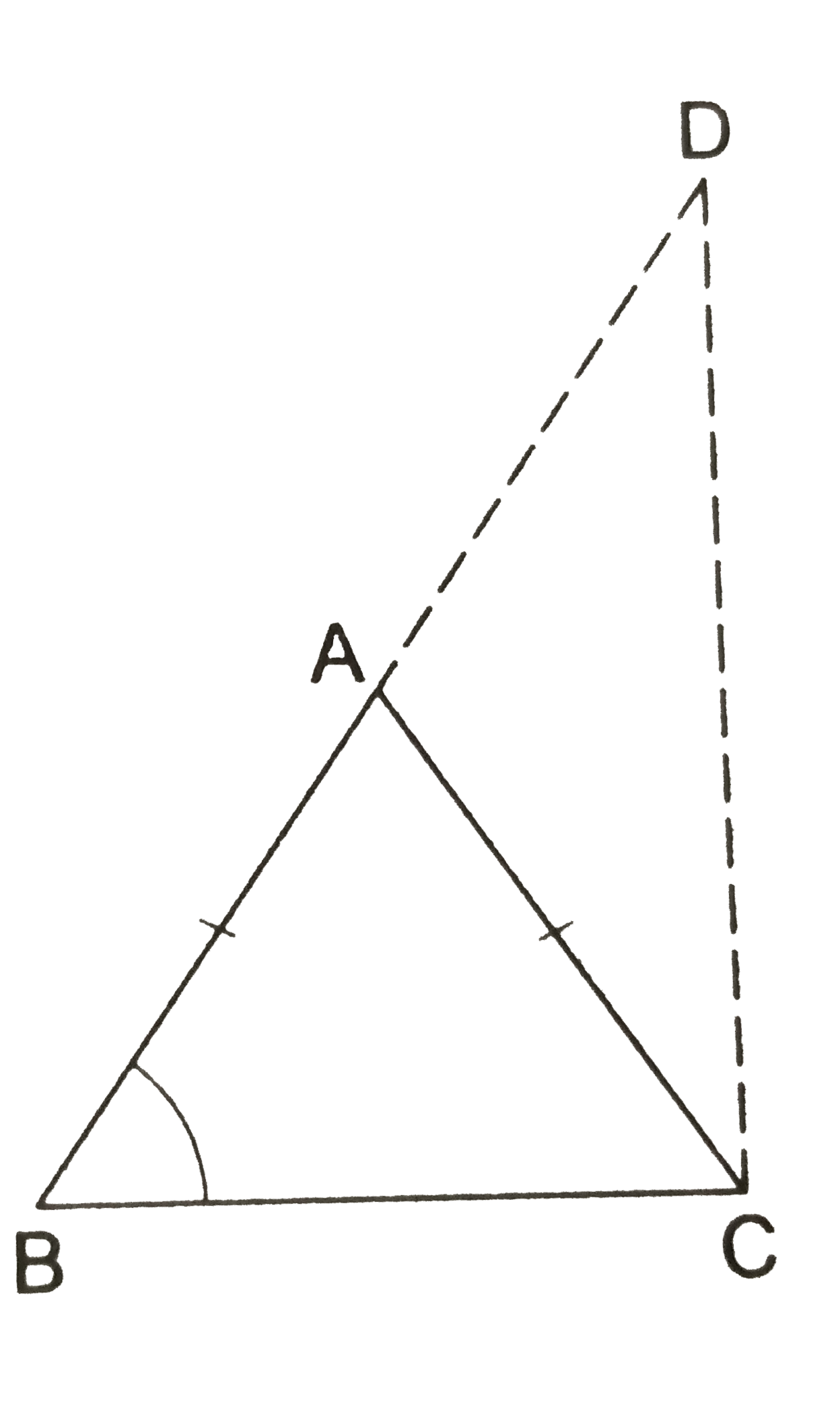
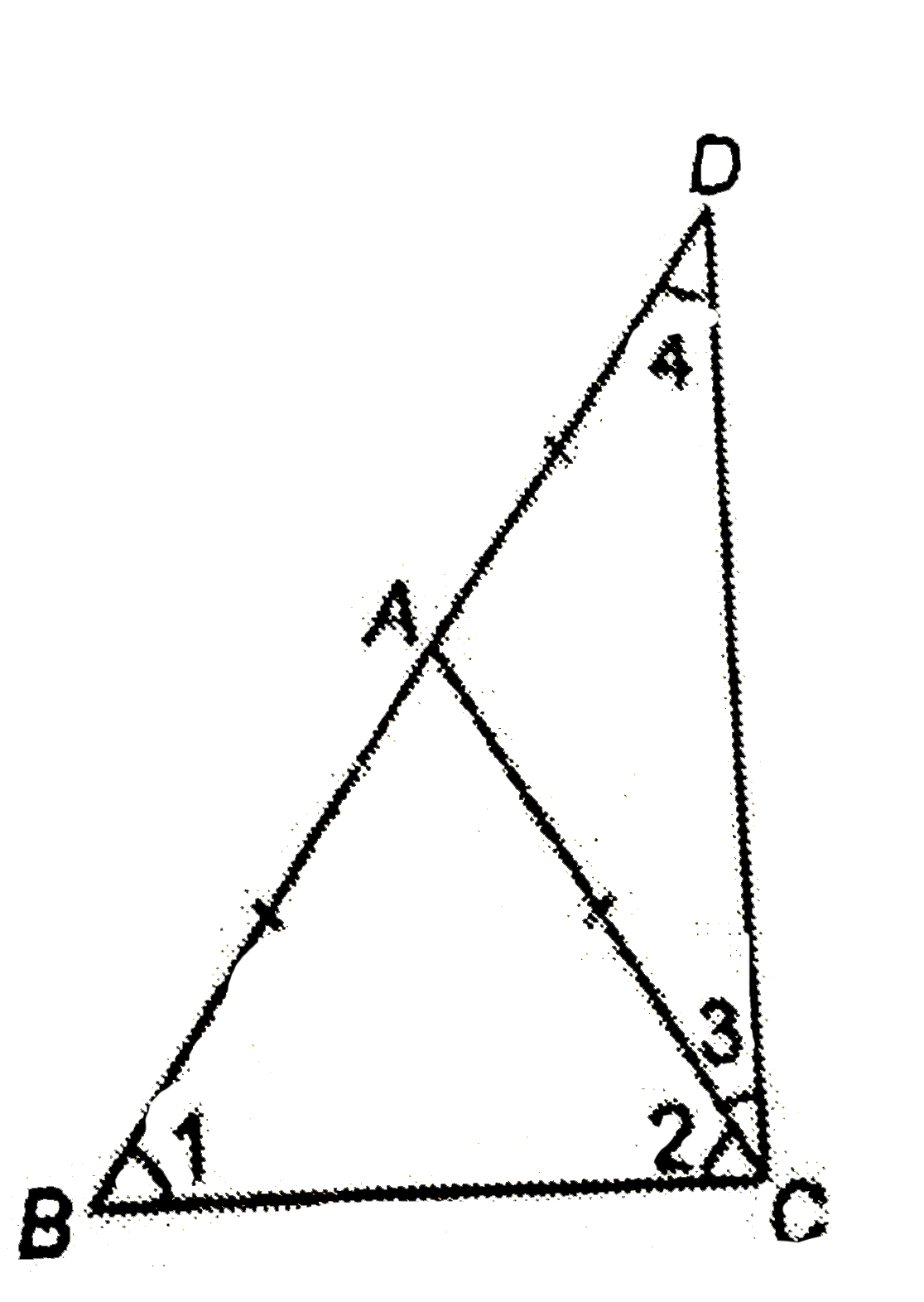
A(a) area ( $Δ B C P)$ = area ( $Δ D P Q)$
B(b) area $(Δ B C P) >$ area ( $Δ D P Q)$
C(c) area $(Δ B C P) <$ area $(Δ D P Q)$
D(d) area $(Δ B C P)$ + area ( $Δ D P Q)$ = area $(Δ B C D)$
$Δ A B C$ is an isosceles triangle with $A B = A C$ , side BA is produced to D such that AB=AD. Prove that $∠ B C D$ is a right angle.
A $60^{\circ}$
B $90^{\circ}$
C $120^{\circ}$
Dcan't be determined
$Δ A B C$ is an isosceles triangle with $A B = A C$ , side BA is produced to D such that AB=AD. Prove that $∠ B C D$ is a right angle.
A $60^{\circ}$
B $90^{\circ}$
C $120^{\circ}$
Dcan't be determined

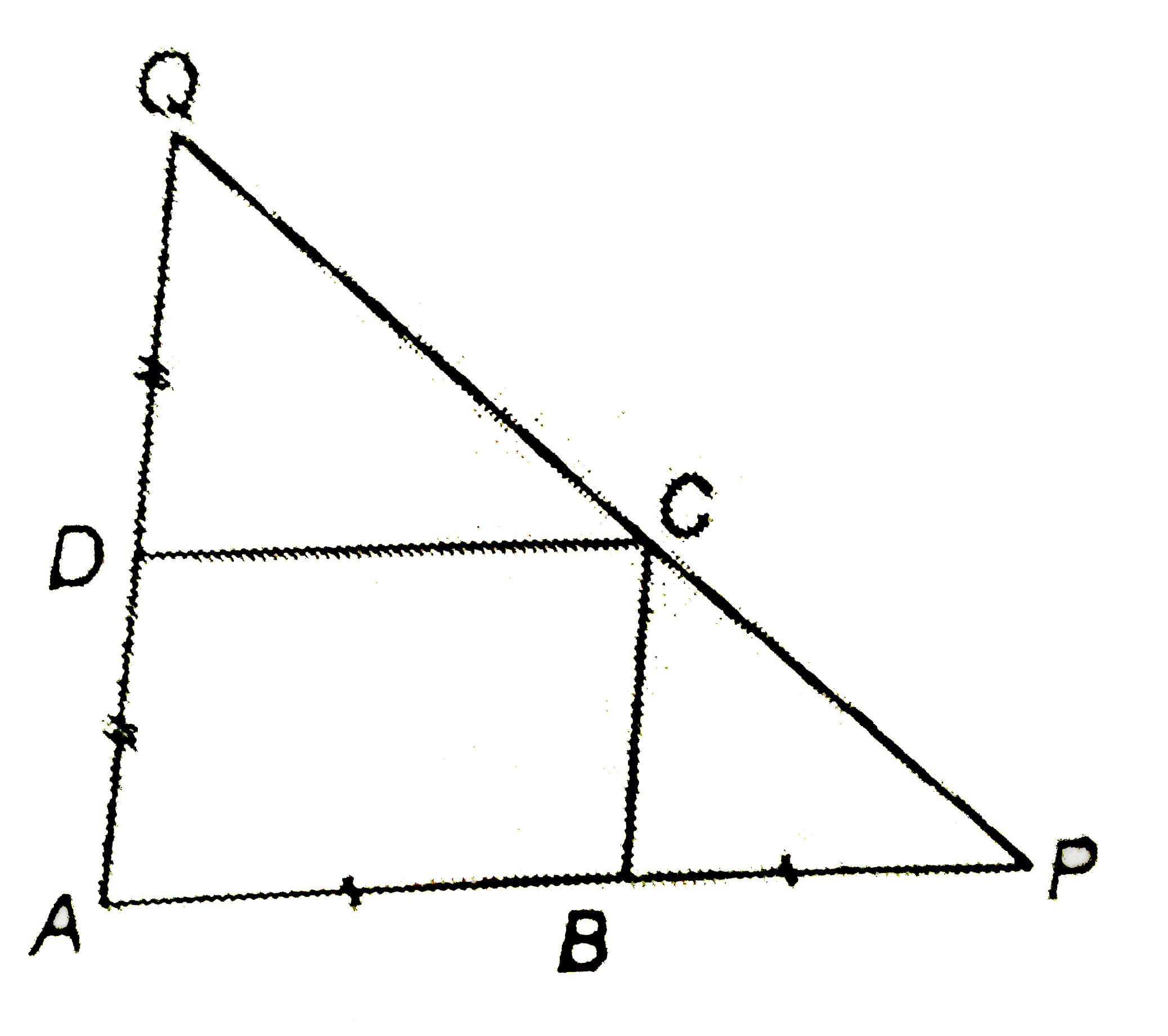
In the adjoining figure, ABCD is a paralogram. The side AB is produced to P such that AB=BP and the side AD is produced to Q such that AD = DQ. Prove that CP = CQ.