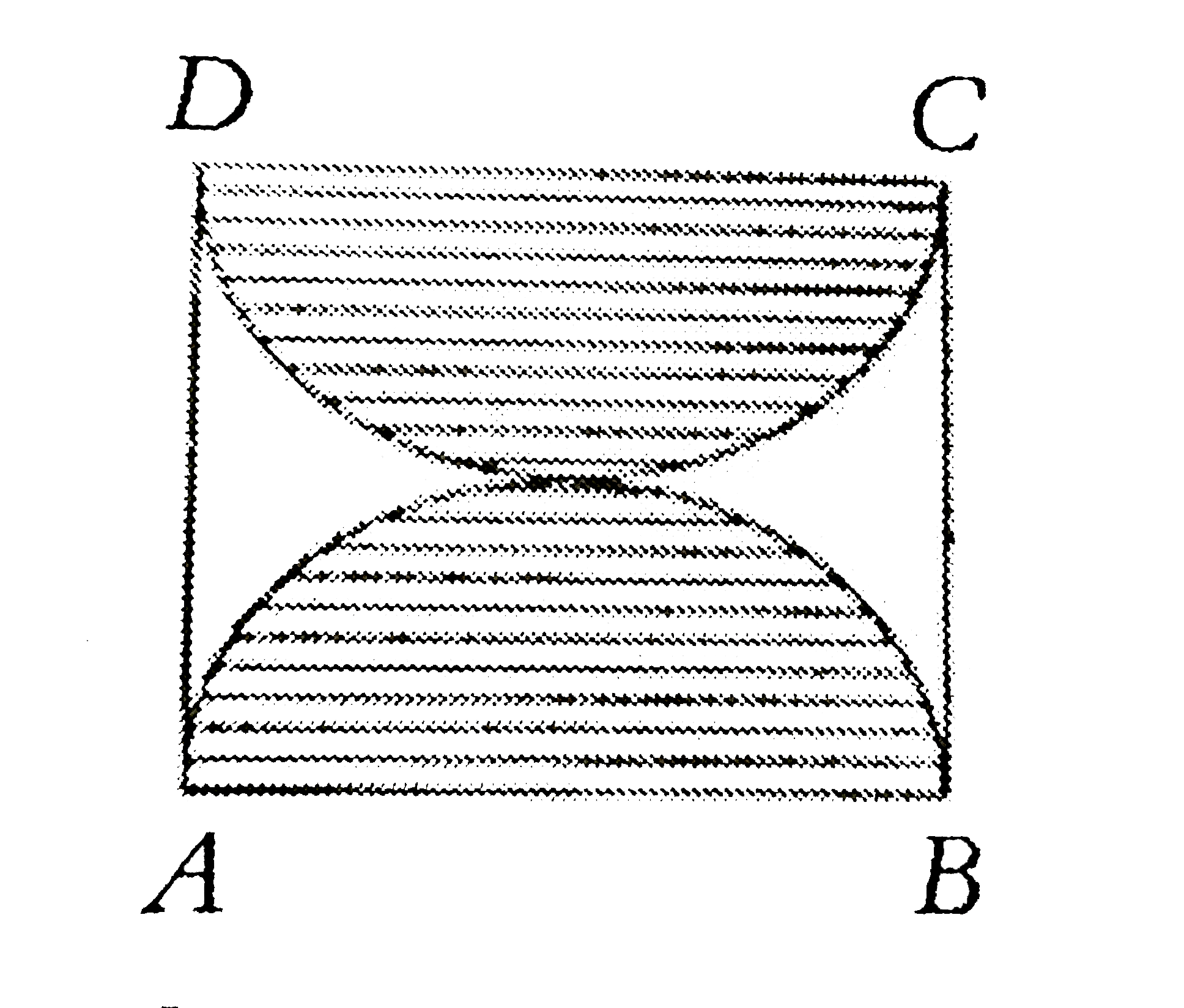
In the adjoining figure, ABCD is a square of side 10 cm and two semicircles with side of the square as diameter. A quarter circle is also seen in figure with side of square as radius. Find the area of the square region excluding the shaded part (deepak). (Take π=3.14)

First of all we will find the area of I and II i.e., Batti of Deepak, draw OM⊥ABandON⊥BC.
∴Ar(I)=ar(sectorNBKO)−ar(ΔBNO)
=π(5)2×90∘360∘−12×5×5
⇒ar(II)=ar(I)
∴ar(I+II)=2(25π4−252)=252(π−2)
=252(3.14−2)=14.25cm2
Now, area of deepak = ar (quadrant APCB) - [ar (semicircle IV+I+II) + ar (semicircle V+I+II) −2×ar(I+II))
=π(10)2×90360−[2×π(5)22−2×14.25]
=25π−(25π−28.5)=28.5cm2
Area of unshaded portion = Area of square - Area of deepak
=(10)2−28.5=100−28.5=71.5cm2

Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A
25 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 B
32 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Long Answer Question
6 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
Knowledge Check
In the adjoining figure, ABCD is a square of side 7 cm and two semicircles are drawn inside of it with AB and CD as diameters. Find the area of the shaded region (in cm2).
 A144 m2B164 m2C184 m2D154 m2
A144 m2B164 m2C184 m2D154 m2In the adjoining figure, ABCD is a square of side 7 cm and two semicircles are drawn inside of it with AB and CD as diameters. Find the area of the shaded region (in cm2).
 A77B154C115.5D38.5
A77B154C115.5D38.5
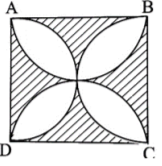
In the given figure, ABCD is a square of side 14cm.Semicircles are drawn with each side of square as diameter. Find the area of the shaded region.
View SolutionIn the given figure, ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter. Find the area of the shaded region.
[ Use π=3.14]

View SolutionIn the figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
View SolutionIn the given figure, ABCd is a square of side 14 cm. Semicricles are drawn with each side of the square as diameter. The area of the shaded region (in cm2) is
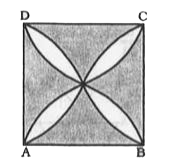
View SolutionABCD is a square of 10 cm and semicircles are drawn with each side of the square as diameter. Find the area of the shaded region. (π=3.14)
View SolutionIn the given figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region. Use π=227.
View Solution

