In the adjoining figure , AM =BM and $∠ B = 90^{\circ} .$ If $∠ B C M = θ$ , then find the values of the following :
(i) $sin θ$ (ii) $tan θ$ (iii) $sec θ$

Video Solution

Text Solution

Verified by Experts

From Pythagoras theorem
$B C^{2} = A C^{2} - A B^{2} = b^{2} - {(2 a)}^{2} = b^{2} - 4 a^{2}$

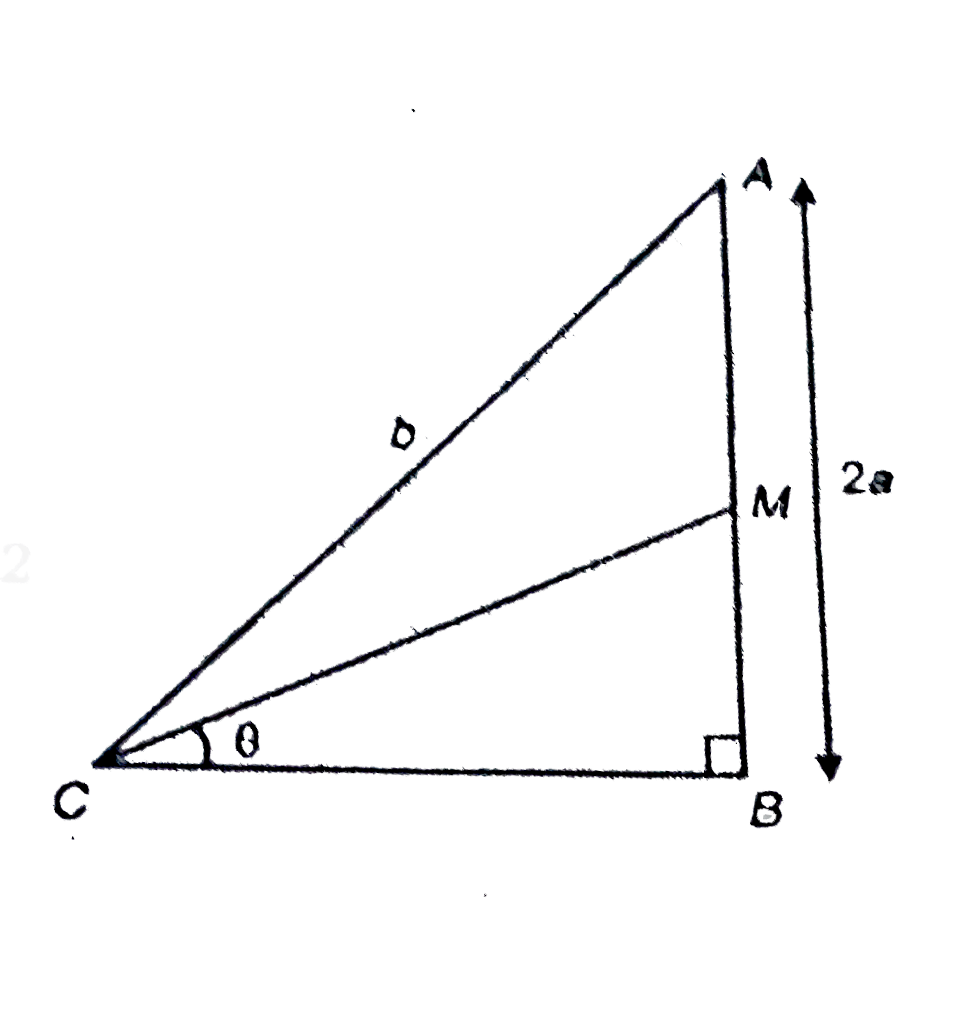
$\Rightarrow B C = \sqrt{b^{2} - 4 a^{2}}$
Now , BM $= \frac{A B}{2} =$
In $Δ B C M$ ,
From Pythagoras theorem
$C M^{2} = B C^{2} + B M^{2} = (b^{2} - 4 a^{2}) + a^{2} = b^{2} - 3 a^{2}$
$\Rightarrow C M = \sqrt{b^{2} - 3 a^{2}}$
(i) $sin θ = \frac{B M}{C M} = \frac{a}{\sqrt{b^{2} - 3 a^{2}}}$
(ii) $tan θ = \frac{B M}{C M} = \frac{a}{\sqrt{b^{2} - 3 a^{2}}}$
(iii) $sec θ = \frac{C M}{B C} = \frac{\sqrt{b^{2} - 3 a^{2}}}{\sqrt{b^{2} - 4 a^{2}}}$

|

Updated on:21/07/2023

Class 10 MATHS TRIGONOMETRIC RATIOS AND IDENTITIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
For the every $θ, 0 < θ \leq 90$ , find the values of the following angle
$2 {sin}^{2} θ - 3 sin θ = - 1$
A $30^{\circ}$
B $45^{\circ}$
C $90^{\circ}$
Dboth (a) and (c)

NAGEEN PRAKASHAN-INTRODUCTION TO TRIGONOMETRY-Revision Exercise Long Answer Questions

Home
Ask Doubt
Profile