In the adjoining figure , ∠AOC=110∘, Calculate :
∠ABC
The correct Answer is:125∘
To solve the problem, we need to calculate the angle ABC given that angle AOC is 110 degrees. Here’s a step-by-step solution:
1. Identify the Given Information:
- We are given that angle AOC = 110 degrees.
2. Understand the Geometry:
- In the figure, O is the center of the circle, and OA, OB, and OC are radii of the circle. Therefore, OA = OB = OC.
3. Construct the Triangles:
- Join points A and B to form triangle OAB and triangle OBC.
4. Use Properties of Isosceles Triangles:
- Since OA = OB, triangle OAB is isosceles. Thus, the angles opposite to equal sides are equal:
- Let angle OAB = angle OBA = X.
5. Apply the Triangle Sum Property:
- In triangle OAB, the sum of angles is 180 degrees:
angle OAB+angle OBA+angle AOB=180∘
Substituting the known values:
X+X+angle AOB=180∘
This simplifies to:
2X+angle AOB=180∘(Equation 1)
6. Determine angle AOB:
- Since OB bisects angle AOC, we have:
angle AOB=12×angle AOC=12×110∘=55∘
7. Substitute angle AOB into Equation 1:
- Now substitute angle AOB into Equation 1:
2X+55∘=180∘
Rearranging gives:
2X=180∘−55∘=125∘
Thus:
X=125∘2=62.5∘
8. Find angle OBC:
- Since triangle OBC is also isosceles (OB = OC), angle OBC will also be:
angle OBC=62.5∘
9. Calculate angle ABC:
- Angle ABC is the sum of angles OBA and OBC:
angle ABC=angle OBA+angle OBC=62.5∘+62.5∘=125∘
Final Answer:
- Therefore, the measurement of angle ABC is 125 degrees.
---
- We are given that angle AOC = 110 degrees.
- In the figure, O is the center of the circle, and OA, OB, and OC are radii of the circle. Therefore, OA = OB = OC.
- Join points A and B to form triangle OAB and triangle OBC.
- Since OA = OB, triangle OAB is isosceles. Thus, the angles opposite to equal sides are equal:
- Let angle OAB = angle OBA = X.
- In triangle OAB, the sum of angles is 180 degrees:
angle OAB+angle OBA+angle AOB=180∘
Substituting the known values:
X+X+angle AOB=180∘
This simplifies to:
2X+angle AOB=180∘(Equation 1)
- Since OB bisects angle AOC, we have:
angle AOB=12×angle AOC=12×110∘=55∘
- Now substitute angle AOB into Equation 1:
2X+55∘=180∘
Rearranging gives:
2X=180∘−55∘=125∘
Thus:
X=125∘2=62.5∘
- Since triangle OBC is also isosceles (OB = OC), angle OBC will also be:
angle OBC=62.5∘
- Angle ABC is the sum of angles OBA and OBC:
angle ABC=angle OBA+angle OBC=62.5∘+62.5∘=125∘
- Therefore, the measurement of angle ABC is 125 degrees.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(A)58videos
CIRCLES
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)10videos
CIRCLES
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)16videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE39videos
CONSTRUCTIONS (CIRCLES)
Similar Questions
In the adjoining figure , ∠AOC=110∘, Calculate :
∠OACView SolutionIn the adjoining figure , ∠AOC=110∘, Calculate :
∠ADCView SolutionIn the given figure, find ∠ABC.
 View Solution
View SolutionIn the adjoining figure PQ = PR and ∠PRQ=70∘ Find ∠QPR.
View SolutionIn the adjoining figure, if ∠ACB=40∘, ∠DPB=120∘, then find ∠CBD.
 View Solution
View SolutionIn the followoing figure , AD is the diameter of the circle with centre O. Chords AB,BC and CD are equal .If ∠DEF=110∘, Calculate :
(i) ∠AEF.
(ii) ∠FAB
(##SEL_RKB_ICSE_MAT_X_C17_E03_002_Q01.png" width="80%">View SolutionIn the adjoining figure, AC is diameter of the circle AB = BC and ∠AED=118∘. Calculate :
∠DEC
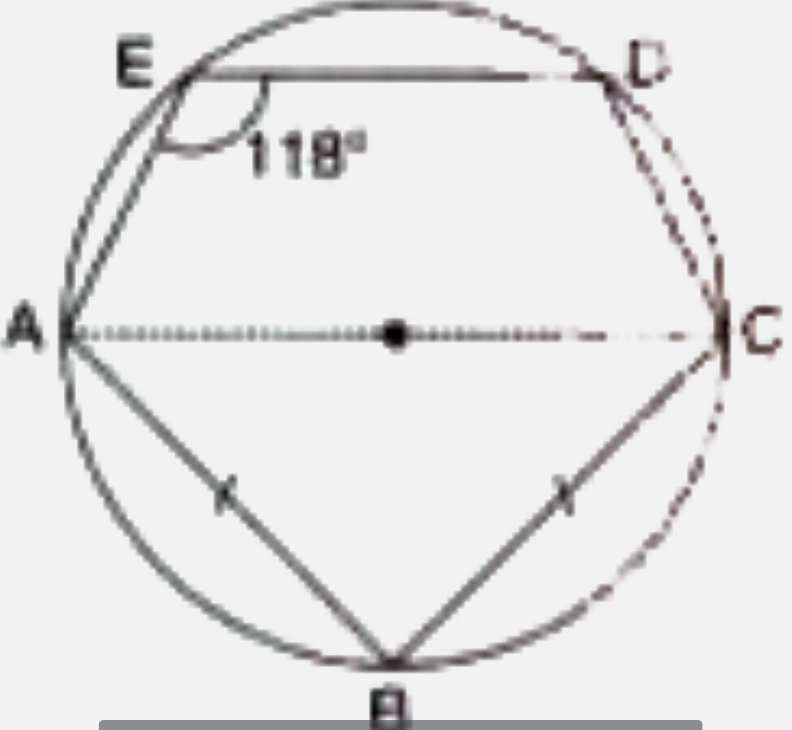 View Solution
View SolutionIn the given figure if find, ∠AOC=45∘, find ∠BOD
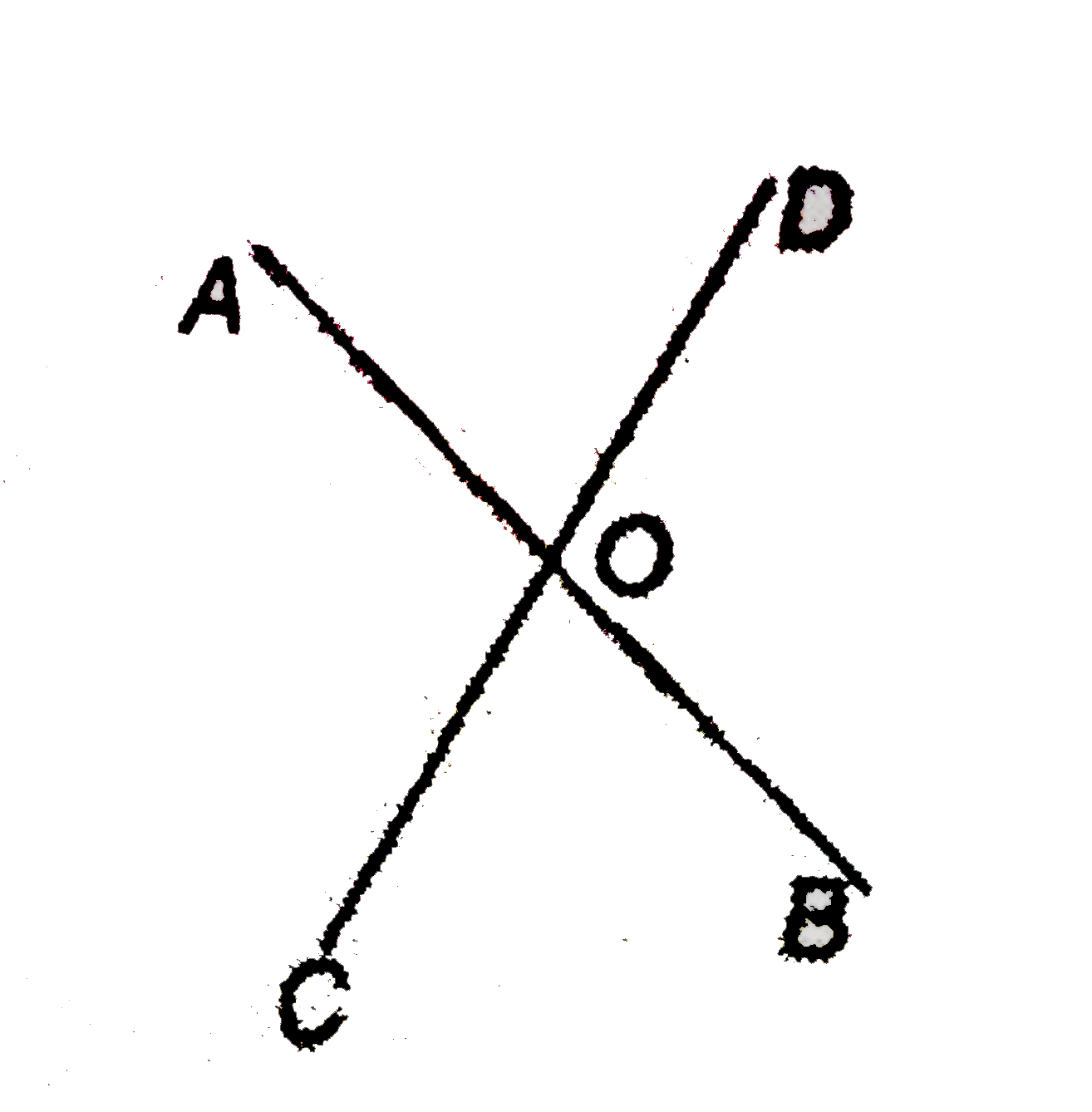 View Solution
View SolutionIn the adjoining figure ∠QPO=24∘ and ∠SPR=20∘ , find the value of ∠QOR.
 View Solution
View SolutionIn the adjoining figure, PS| |QR and ∠Q=115∘, then find the values of ∠P, anl≥R and ∠S.
 View Solution
View Solution

