In the adjoining figure , ∠AOC=110∘, Calculate :
∠OAC
The correct Answer is:35∘
To solve the problem, we need to find the angle OAC given that angle AOC is 110 degrees. Here’s a step-by-step solution:
Step 1: Identify the Triangle
We have a circle with center O, and we know that angle AOC = 110 degrees. We need to find angle OAC.
Step 2: Recognize the Properties of the Triangle
In triangle OAC, we have two sides OA and OC which are equal because they are both radii of the same circle. Therefore, OA = OC.
Step 3: Use the Isosceles Triangle Property
Since OA = OC, triangle OAC is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are also equal. Thus, we can say:
- Angle OAC = Angle OCA.
Let’s denote angle OAC as X. Therefore, we can write:
- Angle OAC = X
- Angle OCA = X
Step 4: Apply the Triangle Sum Property
The sum of the angles in any triangle is 180 degrees. Therefore, we can write the equation:
Angle OAC+Angle OCA+Angle AOC=180∘
Substituting the known values:
X+X+110∘=180∘
Step 5: Simplify the Equation
This simplifies to:
2X+110∘=180∘
Step 6: Solve for X
Now, we can isolate X:
2X=180∘−110∘
2X=70∘
X=70∘2
X=35∘
Step 7: Conclusion
Thus, angle OAC = 35 degrees.
Final Answer
The angle OAC is 35 degrees.
---
We have a circle with center O, and we know that angle AOC = 110 degrees. We need to find angle OAC.
In triangle OAC, we have two sides OA and OC which are equal because they are both radii of the same circle. Therefore, OA = OC.
Since OA = OC, triangle OAC is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are also equal. Thus, we can say:
- Angle OAC = Angle OCA.
- Angle OAC = X
- Angle OCA = X
The sum of the angles in any triangle is 180 degrees. Therefore, we can write the equation:
Angle OAC+Angle OCA+Angle AOC=180∘
Substituting the known values:
X+X+110∘=180∘
This simplifies to:
2X+110∘=180∘
Now, we can isolate X:
2X=180∘−110∘
2X=70∘
X=70∘2
X=35∘
Thus, angle OAC = 35 degrees.
The angle OAC is 35 degrees.
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(A)
58 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
In the adjoining figure , ∠AOC=110∘, Calculate :
∠ADC
View SolutionIn the adjoining figure , ∠AOC=110∘, Calculate :
∠ABC
View SolutionIn the adjoining figure, find AC . (FIGURE)
View SolutionIn the adjoining figure PQ = PR and ∠PRQ=70∘ Find ∠QPR.
View SolutionIn the adjoining figure, if ∠ACB=40∘, ∠DPB=120∘, then find ∠CBD.

View SolutionIn the followoing figure , AD is the diameter of the circle with centre O. Chords AB,BC and CD are equal .If ∠DEF=110∘, Calculate :
(i) ∠AEF.
(ii) ∠FAB
(##SEL_RKB_ICSE_MAT_X_C17_E03_002_Q01.png" width="80%">
View SolutionIn the adjoining figure , ∠BCD=∠ADB (each 90∘) . angle BC= 3 cm and length of side opposite ∠C in ΔBCD is 5 cm , then find the squre root of length of side opposite to ∠D in ΔADB.
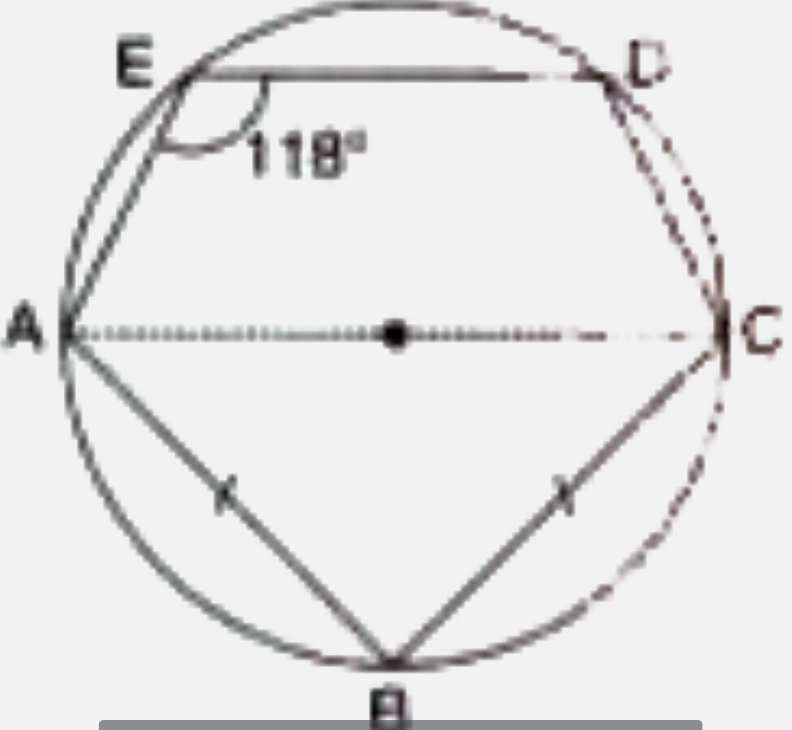
View SolutionIn the adjoining figure, AC is diameter of the circle AB = BC and ∠AED=118∘. Calculate :
∠DEC
View SolutionIn the given figure if find, ∠AOC=45∘, find ∠BOD
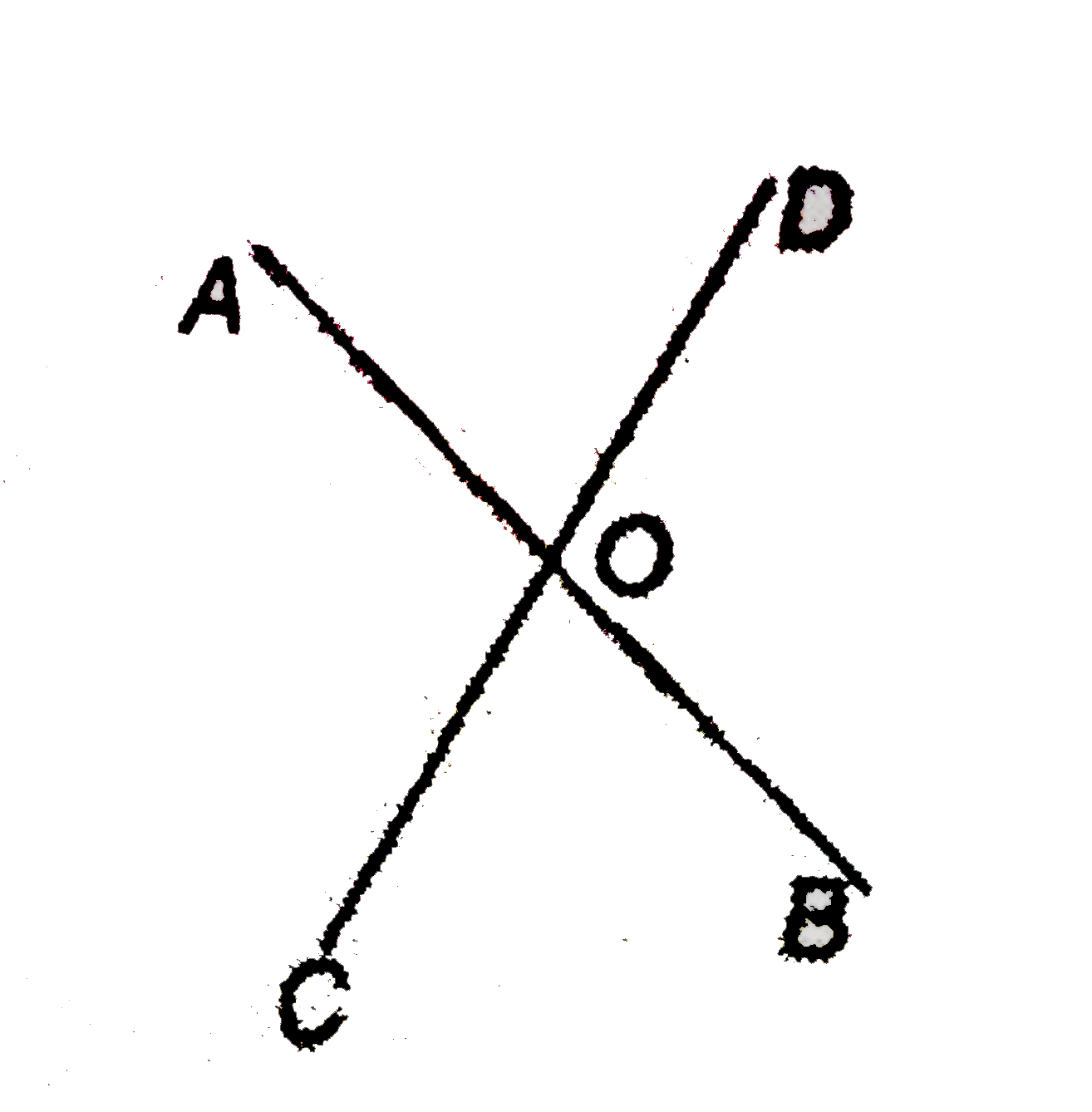
View SolutionIn the adjoining figure ∠QPO=24∘ and ∠SPR=20∘ , find the value of ∠QOR.

View Solution