In the adjoining figure , ∠BCD=∠ADB (each 90∘) . angle BC= 3 cm and length of side opposite ∠C in ΔBCD is 5 cm , then find the squre root of length of side opposite to ∠D in ΔADB.
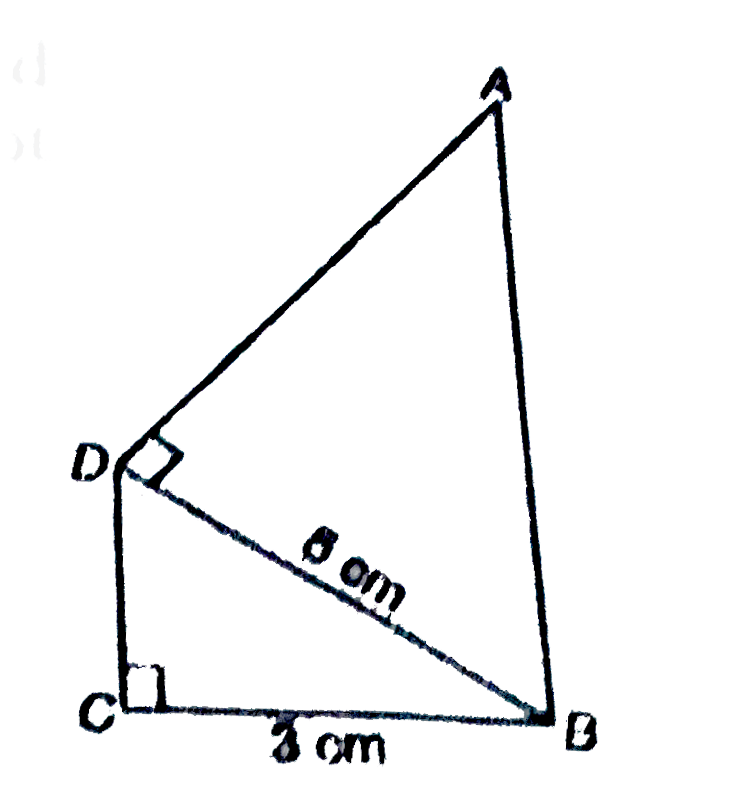
Draw DE botAB<br>∈rightDeltaBCD,byPythagorastheorem,<br>DC^(2)=DB^(2)-BC^(2)=25-9=16<br>:. DC=sqrt(16)=4cm<br>:.EB=DC=4cm<br>AlsoDE=BC=3cm<br>LetAE=xcmandAD=ycm<br>InrightDeltaAED,byPythagorastheorem,<br>AD^(2)=AE^(2)+DE^(2)<br>rArr y^(2)=x^(2)+9InrightDeltaADB,byPythagorastheorem,<br>AB^(2)=AD^(2)+DB^(2)<br>rArr(x+4)^(2)=y^(2)+25<br>rArrx^(2)+8x+16=(x^(2)+9)+25[om(1)]<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NTN_MATH_X_C08_S01_016_S02.pngwh=80%mx-autosty≤=background:white;><br>rArr8x=18<br>:. x=(18)/(8)=2.25cm<br>:. AB=x+4=6.25cm<br>:. sqrt(AB)=sqrt(6.25)=2.5cm
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Problems From NCERT/exemplar29videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8a20videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - PROBLEMS FROM NCERT/ EXEMPLAR10videos
CONSTRUCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions8videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the ajoining figure the angle BAC and ∠ADB are right angles .
BA=5cm,AD=3cmandBD=4cm, what is the length of DC ?
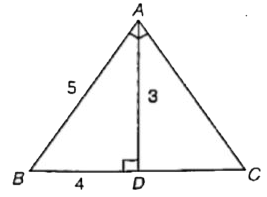 A2.5B3C2.25D2
A2.5B3C2.25D2
In the adjoining figure, AP=8cm, BP=2cm and ∠CPA=90∘. Find the length of chord CD.
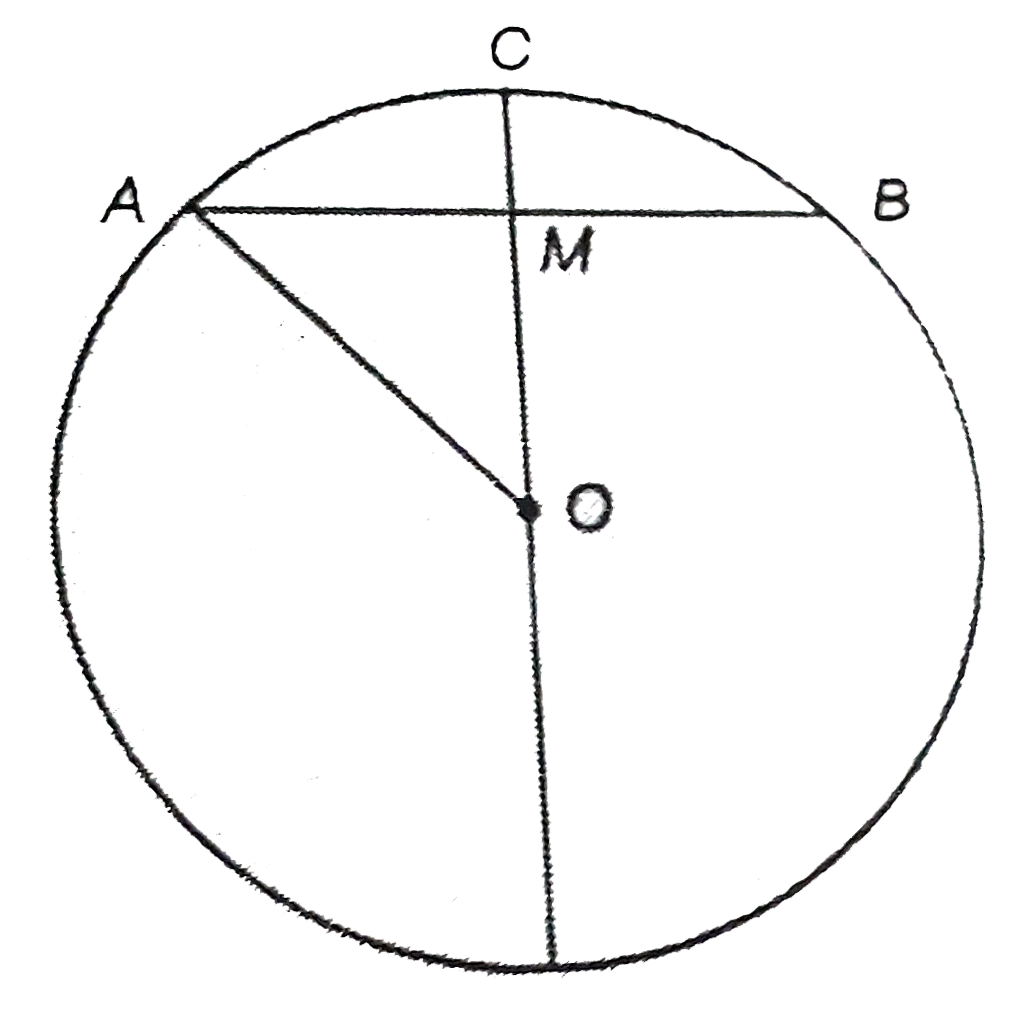 View Solution
View SolutionIn the adjoining figure, AP=8cm, BP=2cm and ∠CPA=90∘. Find the length of chord CD.
 View Solution
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.
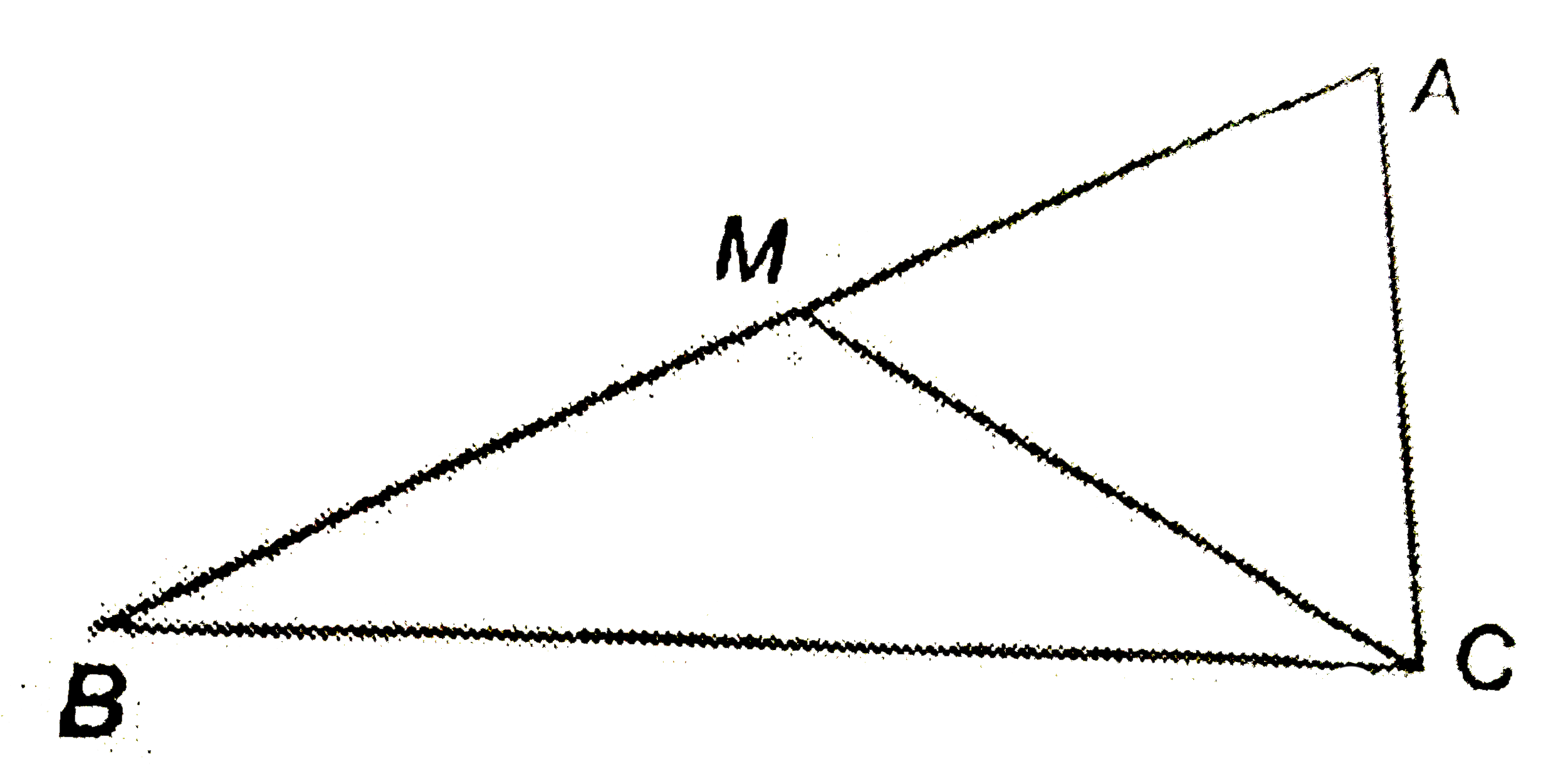 View Solution
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.
 View Solution
View SolutionIn the following figure, ∠ABC=90∘ AB = (x+8) cm , BC = (x+ 1) cm and AC = (x+15) cm.
Find the lengths of the sides of the triangles.
 View Solution
View SolutionIn a right angled triangle ABCABC=90∘,ACB=30∘ and AB=8cm. Find the length of the other sides of the triangle.
View Solution