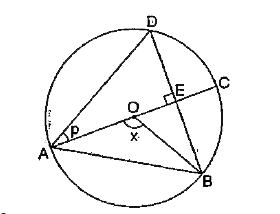
In the adjoining figure, BD is the diameter of the circle which bisects the chord AC at point E. If , , then find the radius of the circle.

Let radius
Now,
( The line segment joining the centre to mid-point of a chord is perpendicular to the chord)
In ,
(by Pythagoras theorem)
Radius of circle =5 cm .
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
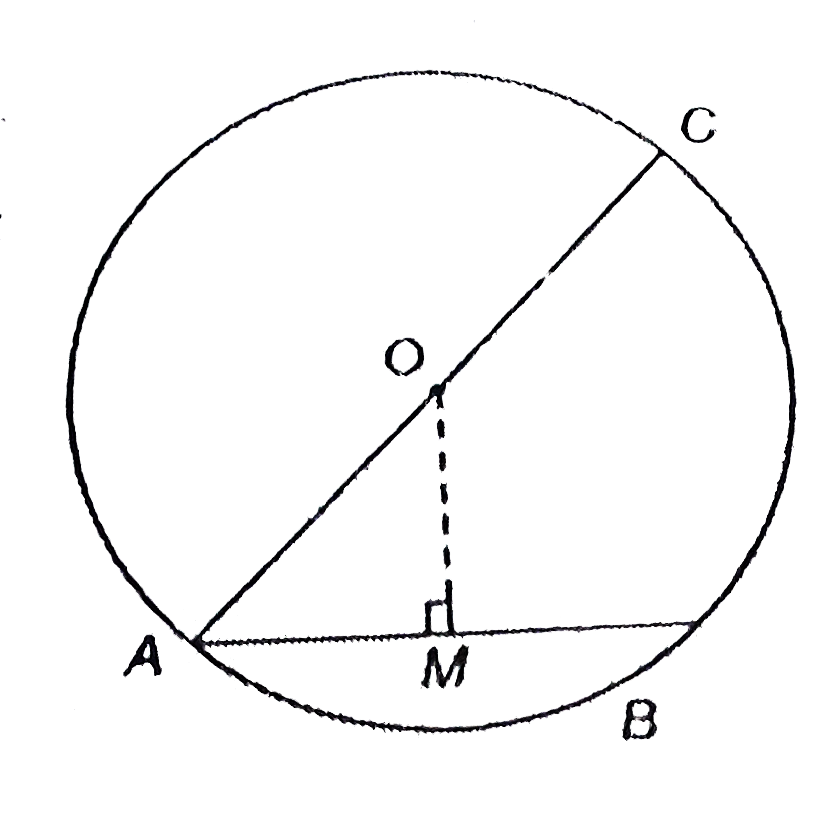
In the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
View Solution
Knowledge Check
In the adjoining figure BD is the diameter of the circle and ∠BCA=41∘. Find ∠ABD:
 A41∘B49∘C22.5∘D20.5∘
A41∘B49∘C22.5∘D20.5∘In the adjoining figure, O is the centre of circle and diameter AC=26cm. If chord AB=10cm, then the distance between chord AB and centre O of the circle is :
 A24 cmB16 cmC12 cmDnone of the above
A24 cmB16 cmC12 cmDnone of the aboveIn a class of 39 students the ratio of boys and girls is 2 : 1. Radhika ranks 15th among all the students from top and 8th among girls from bottom. How many boys are there below Radhika ?
AA) 9BB) 17CC) 11DD) 15
In the adjoining figure, AC is the diameter of the circle. If ∠BDC=115∘, then find the value of ∠ACB.
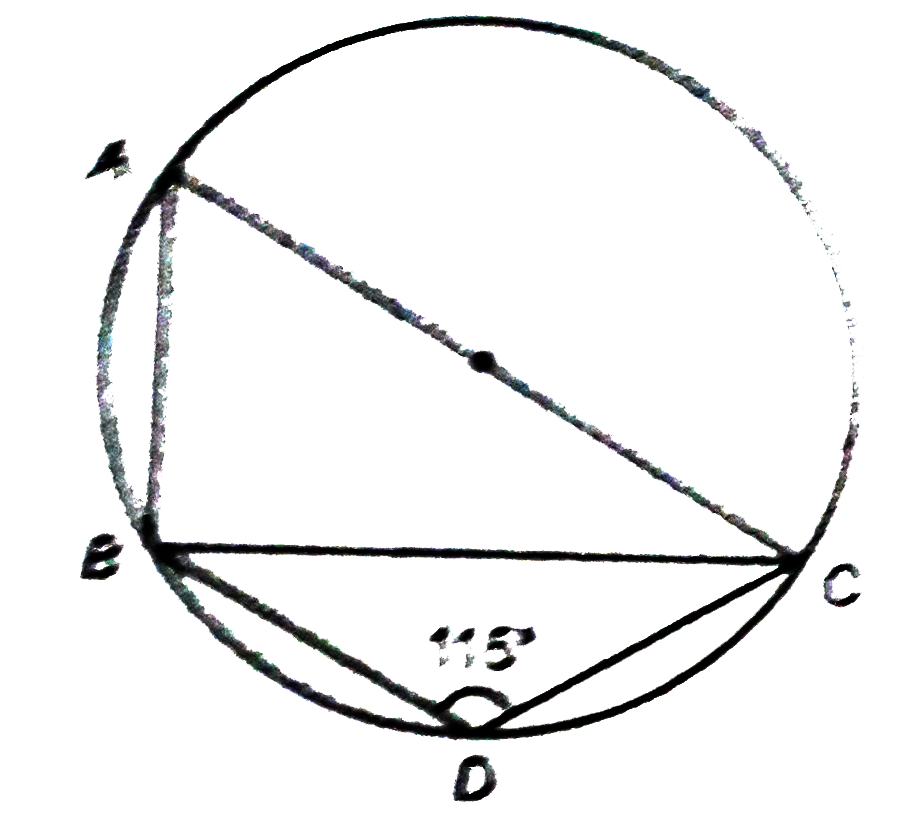
View SolutionIn the figure (i) given below, O is the centre of the circle. AB and CD are the chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB=24 cm OM=5 cm, ON=12 cm. Find the, (i) radius of the circle (ii) length of chord CD (ii) In the figure (ii) given below, CD is diameter which meets the chord AB at E such that AE = BE = 4 cm.If CE = 3 cm, find the radius of the circle.
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View Solutionin the adjoining figure ABCD is a square of side 14 cm. Find the radius of the circle

View SolutionIn the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
View Solution
