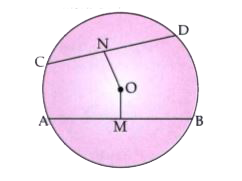
In the figure (i) given below, O is the centre of the circle. AB and CD are the chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB=24 cm OM=5 cm, ON=12 cm. Find the, (i) radius of the circle (ii) length of chord CD (ii) In the figure (ii) given below, CD is diameter which meets the chord AB at E such that AE = BE = 4 cm.If CE = 3 cm, find the radius of the circle.
In △OAM
OA2=OM2+AM2
r2=52+122
r2=169
r=13
In△ONC
OC2=ON2+NC2
NC2=169−144
NC=5
So,
CD=10cm
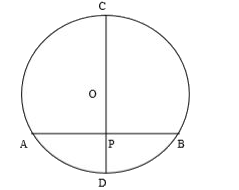
In△OBE
OB2=OE2+BE2
r2=(r−3)2+42
solving this we get
r=256cm
Similar Questions
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
View SolutionIn the figure, given alongside, CD is a diameter which meets the chord AB at E, such that AE = BE = 4 cm. If CE is 3 cm, find the radius of the circle.
View Solution
Knowledge Check
O' is the centre of the circle, AB is a chord of the circle, OM⊥AB. If AB=20cm,OM=2√11 cm, then radius of the circle is
A15 cmB12 cmC10 cmD11 cm
In the figure given below, CD is the diameter of the circle which meets the chord AB at P such that AP = BP = 12 cm. If DP = 8 cm, find the radius of the circle.
View SolutionIn the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
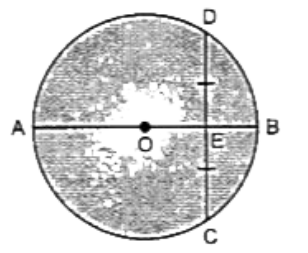
View SolutionThe figure, given below, show a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm. Find the radius of the circle.
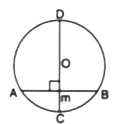
View SolutionIn the given figure, the diameter CD of a circle with centre 0 is perpendicular to the chord AB.
If AB = 8 cm and CM = 2 cm, find the radius of the circle.
View SolutionIn the figure given below, O is the center of the circle. Chord CD is parallel to the diameter AB. If ∠ABC=35∘ , calculate ∠CED.
View SolutionAB and CD are parallel chords of a circle 3 cm apart. If AB = 4 cm, CD = 10 cm, then what is the radius of the circle ?
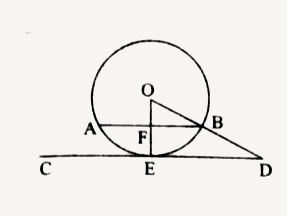
View SolutionIn the figure above, O is the centre of the circle CD is a tangent to the circle at E. OE bisects the chord AB at F. AB = 16 cm and EF = 2 cm. Find the length of DE (in cm).
View Solution
