In the adjoining figure, BD is the diameter of the circle which bisects the chord AC at point E. If AC=8cm, BE=2cm, then find the radius of the circle.

Let radius OA=OB=r
OE=OB−EB
=(r−2)cm
AE=AC2=82=4cm
Now, ∠OEA=90∘
(∵ The line segment joining the centre to mid-point of a chord is perpendicular to the chord)
∴ In ΔOAE,
OA2=OE2+AE2 (by Pythagoras theorem)
⇒r2=(r−2)2+42
⇒r2=r2−4r+4+16
⇒4r=20cm
⇒=5cm
∴ Radius of circle =5 cm .
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
In the given figure, the diameter CD of a circle with centre 0 is perpendicular to the chord AB.
If AB = 8 cm and CM = 2 cm, find the radius of the circle.
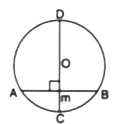
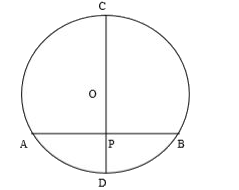
View SolutionIn the figure given below, CD is the diameter of the circle which meets the chord AB at P such that AP = BP = 12 cm. If DP = 8 cm, find the radius of the circle.
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

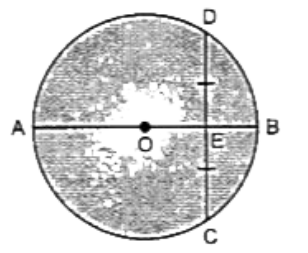
View SolutionThe figure, given below, show a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm. Find the radius of the circle.
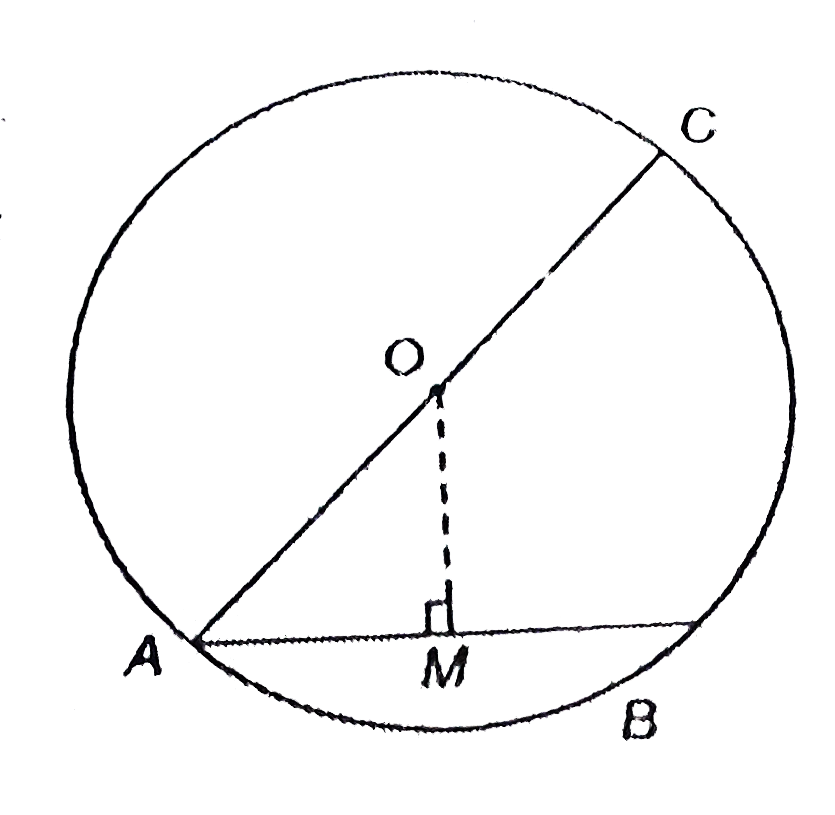
View SolutionIn the adjoining figure,AB is the diameter of the circle of centre O & the chord CD is equal to radius. If P is an external point, then find the value of ∠APB.
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
View SolutionIn the adjoining figure, AC is the diameter of the circle. If ∠BDC=115∘, then find the value of ∠ACB.
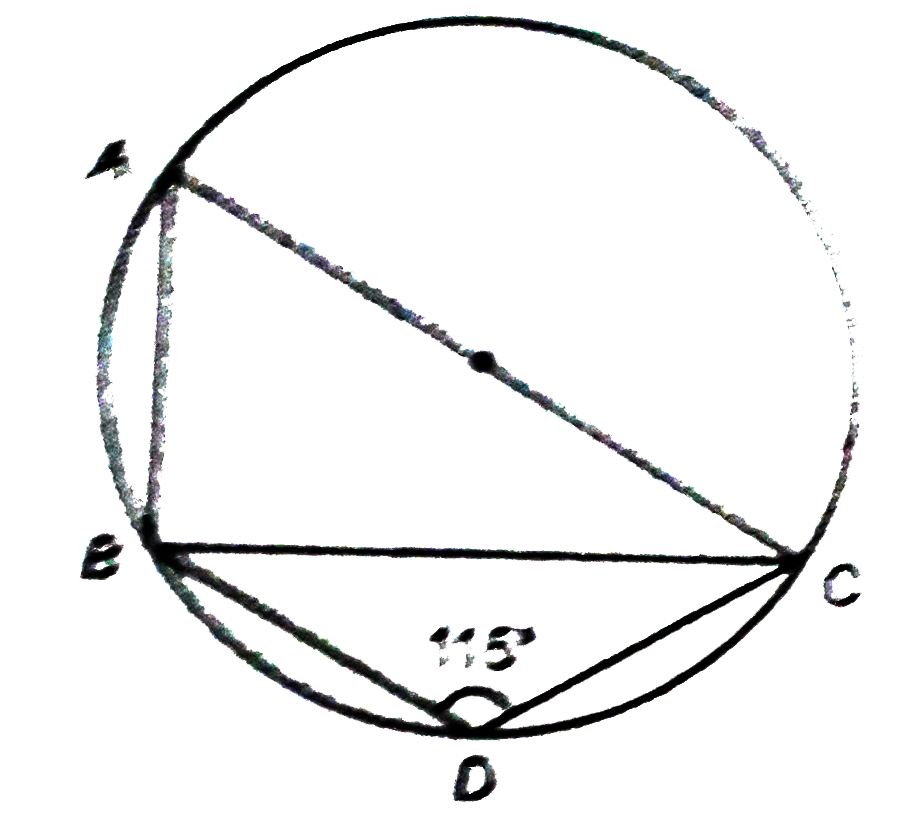
View SolutionThe diameter of a circle is 9 cm, find its radius.
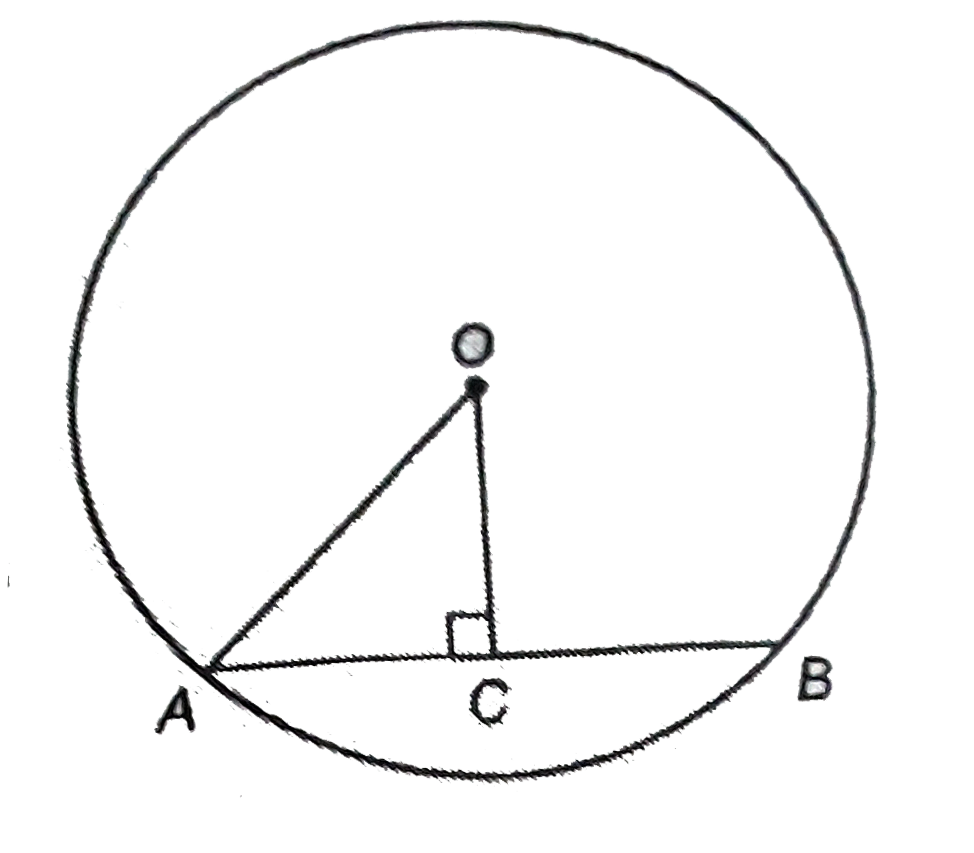
View SolutionIn the adjoining figure O is the centre of circle and c is the mid point. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
View Solution
