In the adjoining figure, CM = 5 cm, RB = 9 cm, CD⊥AB, O is the centre of larger circle and K is the centre of smaller circle. Find the area of shaded region
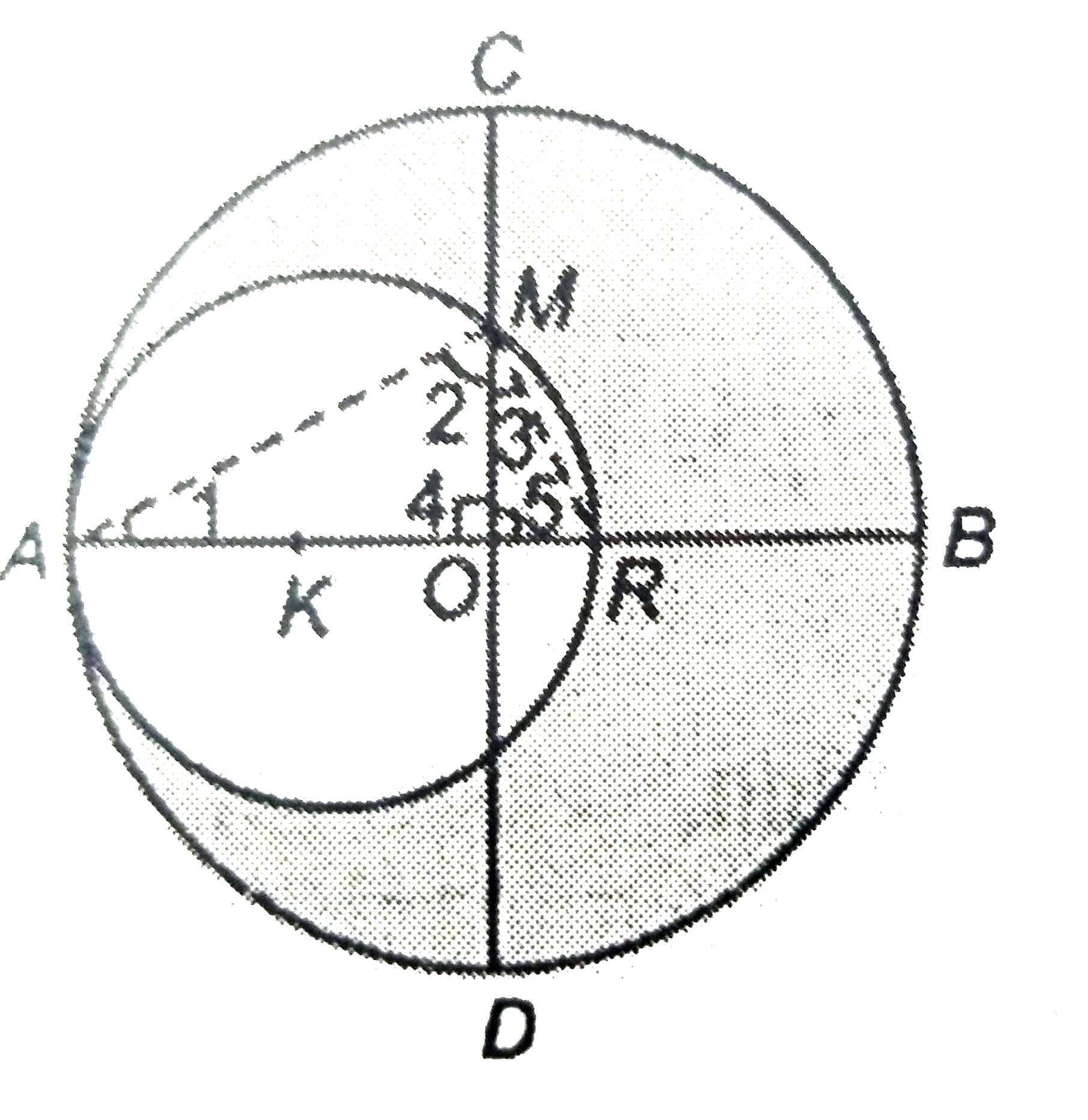
Let radius of larger circle be R and the radius of smaller circle is r.
Since, CM=5cm
∴MO=R−5
Also OB=RandRB=9
∴OR=R−9
In ΔAOM,
∠1+∠2=90∘...(1)
In ΔAMR,
∠2+∠3=90∘ (angle in a semicircle is right angle) ..(2)
From eqs. (1) and (2), we get
∠1+∠2=∠+∠3
⇒∠1=∠3
In ΔsAMOandMOR
∠1=∠3 (just proved)
∠4=∠5 (each 90∘)
∴ΔAMO~ΔMRO (AA corollary)
∴MORO=AOMO
⇒R−5R−9=RR−5
⇒(R−5)2=R(R−9)⇒R2+25−10R=R2−9R
⇒R=25cm
Now, 2R−9=2r⇒2r=41
⇒r=20.5cm
∴ Required area =πR2−πr2=π(R+r)(R−r)
=227×45.5×4.5=643.5cm2
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Problems From NCERT /exemplar
25 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A
25 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
Knowledge Check
In the adjoining figure ABC is an equilateral triangle and C is the centre of the circle, A and B lie on the circle. What is the area of the shaded region , if the diameter of the circle is 28 cm ?
 A(10223−49√3)cm2B(10323−98√3)cm2C(109−38√3)cmDnone of the above
A(10223−49√3)cm2B(10323−98√3)cm2C(109−38√3)cmDnone of the above
In the given figure PQ=24cm,PR=78cm and O is the centre of the circle. Find the area of the shaded region. [Take π=3.14]
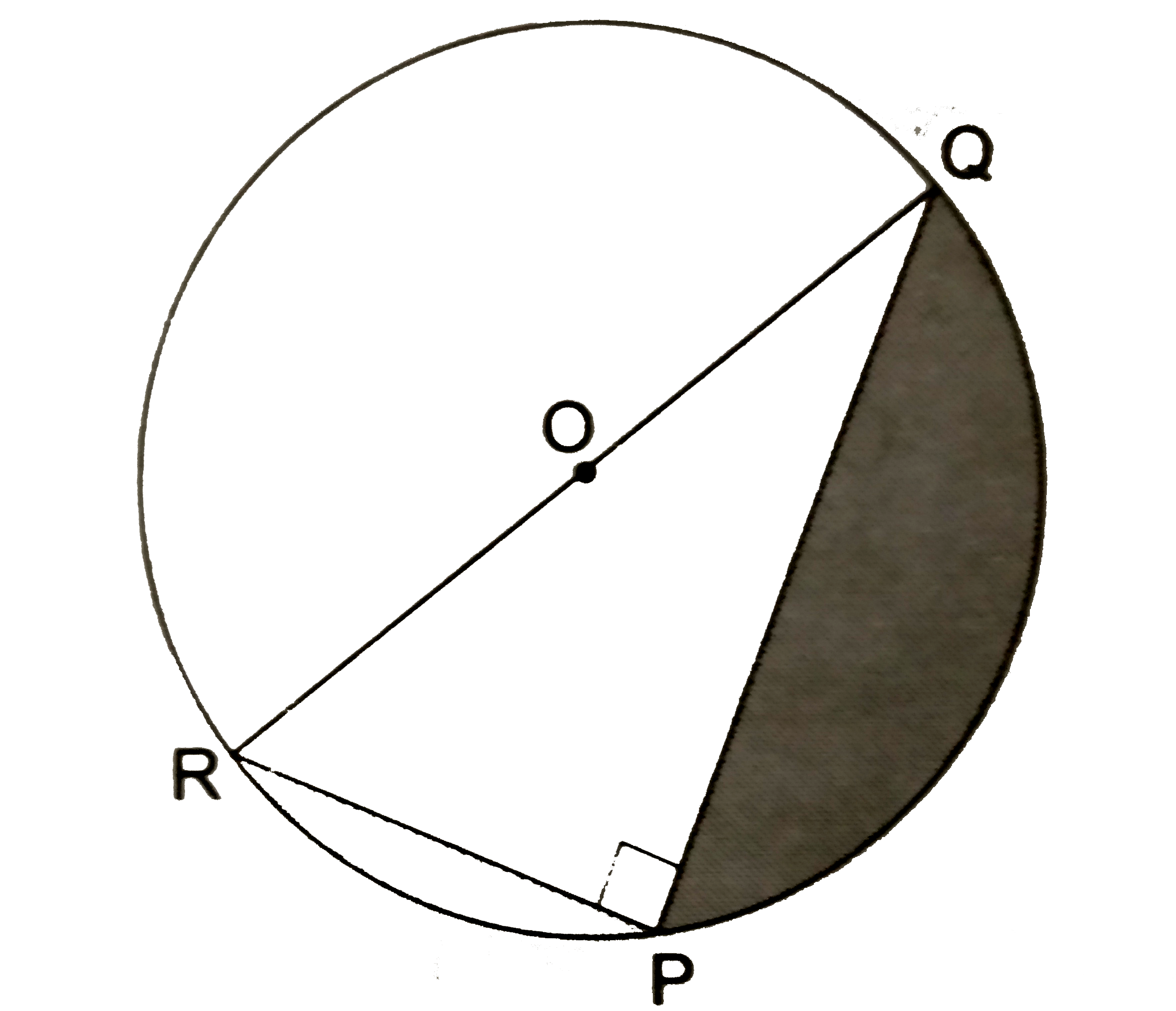
View SolutionIn the given figure, PQ = 24 cm PR = 7 cm and O is the centre of the circle. Find the area of the shaded region. (Use π=3.14)

View SolutionIn the given figure, PQ = 24 cm PR = 7 cm and O is the centre of the circle. Find the area of the shaded region. (Use π=3.14)

View SolutionIn Figure , O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90°. Find the area of the shaded region.[Useπ=3⋅14]
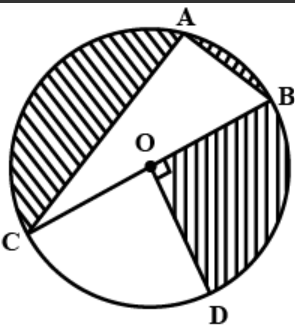
View SolutionIn Figure , O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90°. Find the area of the shaded region.[Useπ=3⋅14]

View SolutionIn Fig. 12-34, O is the centre of a circle such that diameter AB=13 cm and AC=12 cm. BC is joined. Find the area of the shaded region.
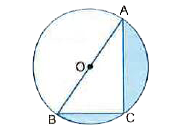
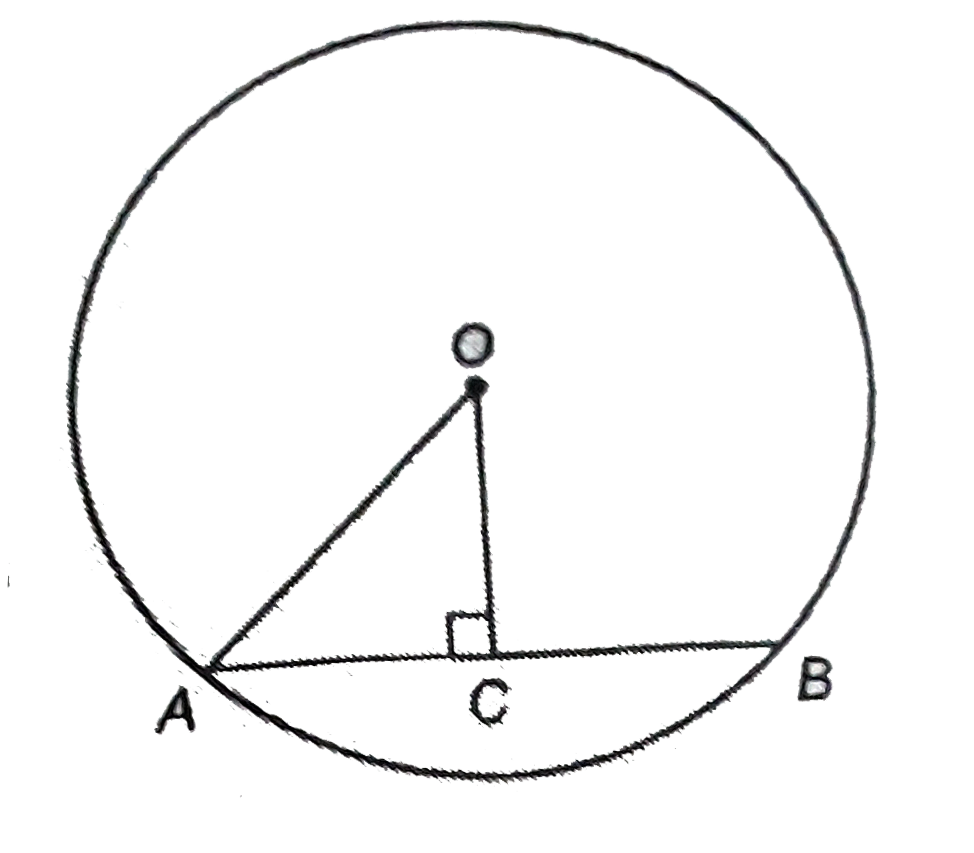
View SolutionIn the adjoining figure O is the centre of circle and c is the mid point. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
View Solution
