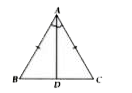
In the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
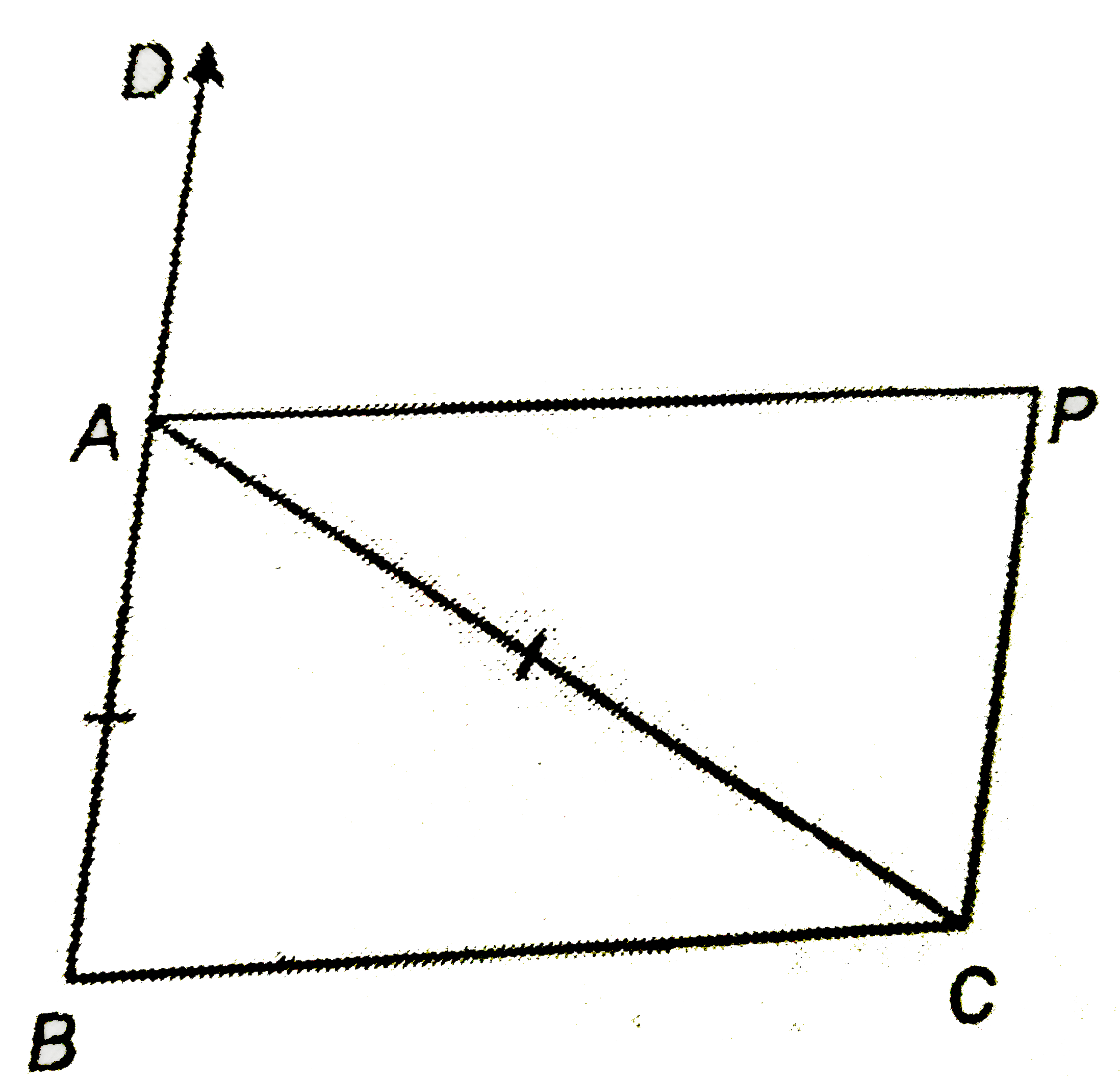
Step by step video, text & image solution for In the adjoining figure, DeltaABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Delta ABC. Prove that anglePAC=angleBCAand squareABCP is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b15videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)10videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise10videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
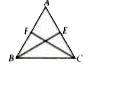 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of these - Question 2 - Select One
In the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
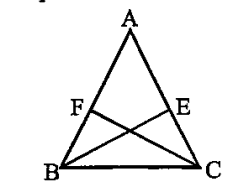 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
In the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
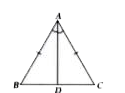
∠B=∠CView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. If BM⊥ACandCN⊥AB, prove that:
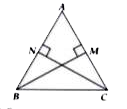
BM = CNView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
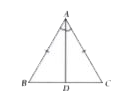
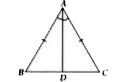
ΔADB≅ΔADCView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
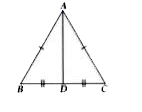 Prove that:
Prove that:
ΔADB≅ΔADCView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
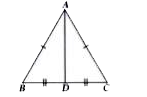 Prove that:
Prove that:
∠BAD=∠CADView SolutionIn the figure, ABC is an isosceles triangle in which AB = AC and LM is parallel to BC. If ∠A=50∘ find ∠LMC.
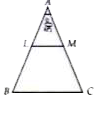 View Solution
View Solution