In the adjoining figure, ΔABC is an isosceles triangles in which AB=AC and AD is the bisector of ∠A. Prove that :
(i) ΔADB≅ΔADC
(ii) ∠B=∠C
(iii) BD=DC
(iv) AD⊥BC

Step by step video & image solution for In the adjoining figure, DeltaABC is an isosceles triangles in which AB=AC and AD is the bisector of angleA. Prove that : (i) DeltaADB~=DeltaADC (ii) angleB=angleC (iii) BD=DC (iv) ADbotBC by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
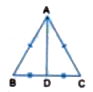
In the adjoining figure, ΔABC is an isosceles triangles in which AB=AC and AD is a median. Prove that :
(i) ΔADB≅ΔADC
(ii) ∠BAD=∠CAD
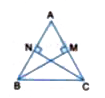
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB=AC. If BM⊥AC and CN⊥AB, prove that :
(i) ΔBMC≅ΔCNB
(ii) BM=CN
View SolutionIn the given figure, AB=CD and AD=CB. Prove that :
(i) ΔABD=ΔCDB
(ii) ∠A=∠C

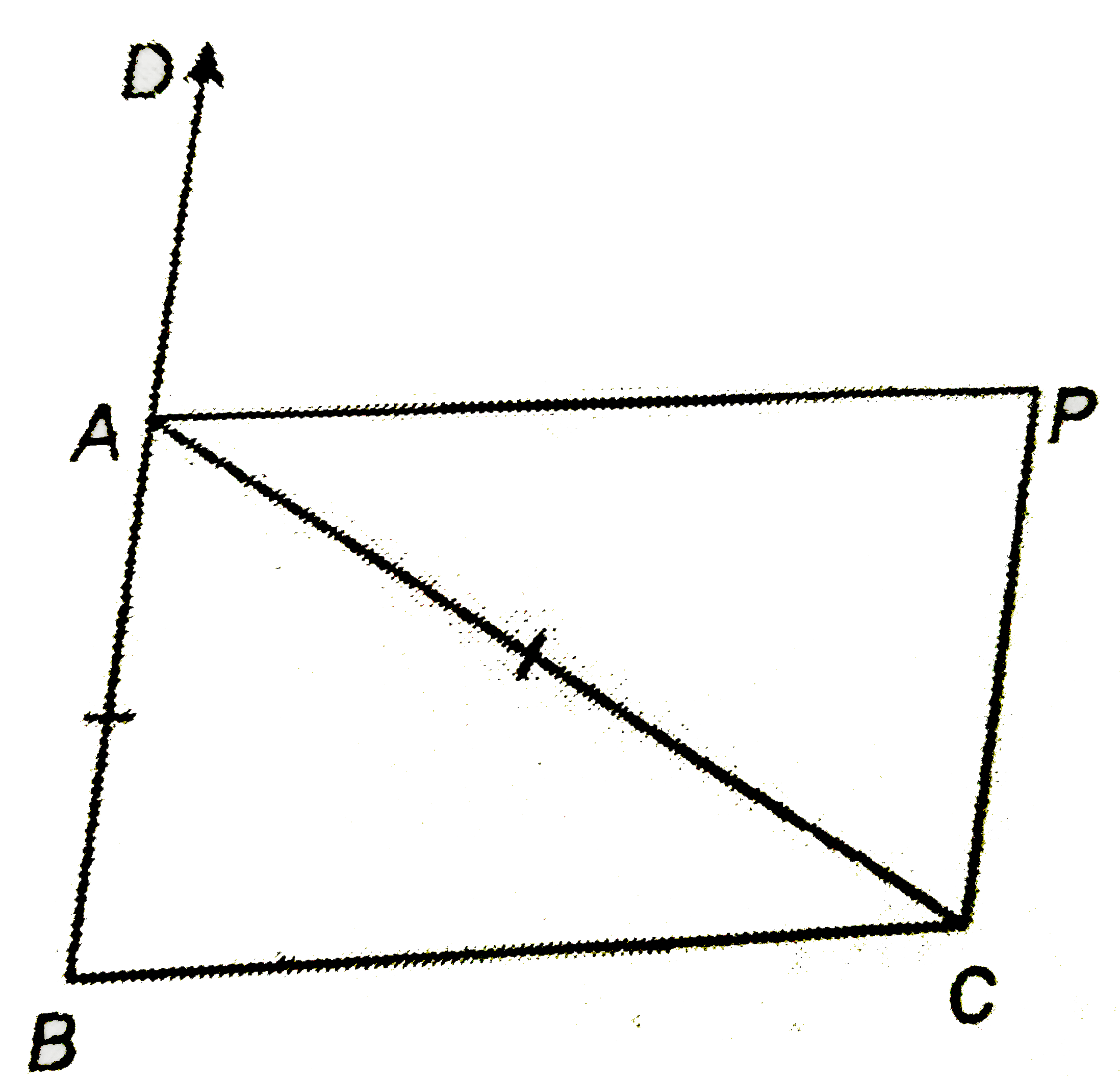
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
View SolutionGiven a ΔABD in which AB=AD and AC bisects BD. Prove that :
ΔABC≅ΔADC.
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
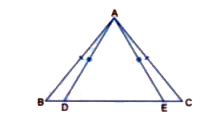
View SolutionIn the given figure AB=AC and AD=AE. Prove that (i) ΔABD≅ΔACE and (ii) BE=DC
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
View SolutionIn the adjoining figure, AD=DC and DB bisects ∠ADC. Prove that ΔADB≅ΔCDB.
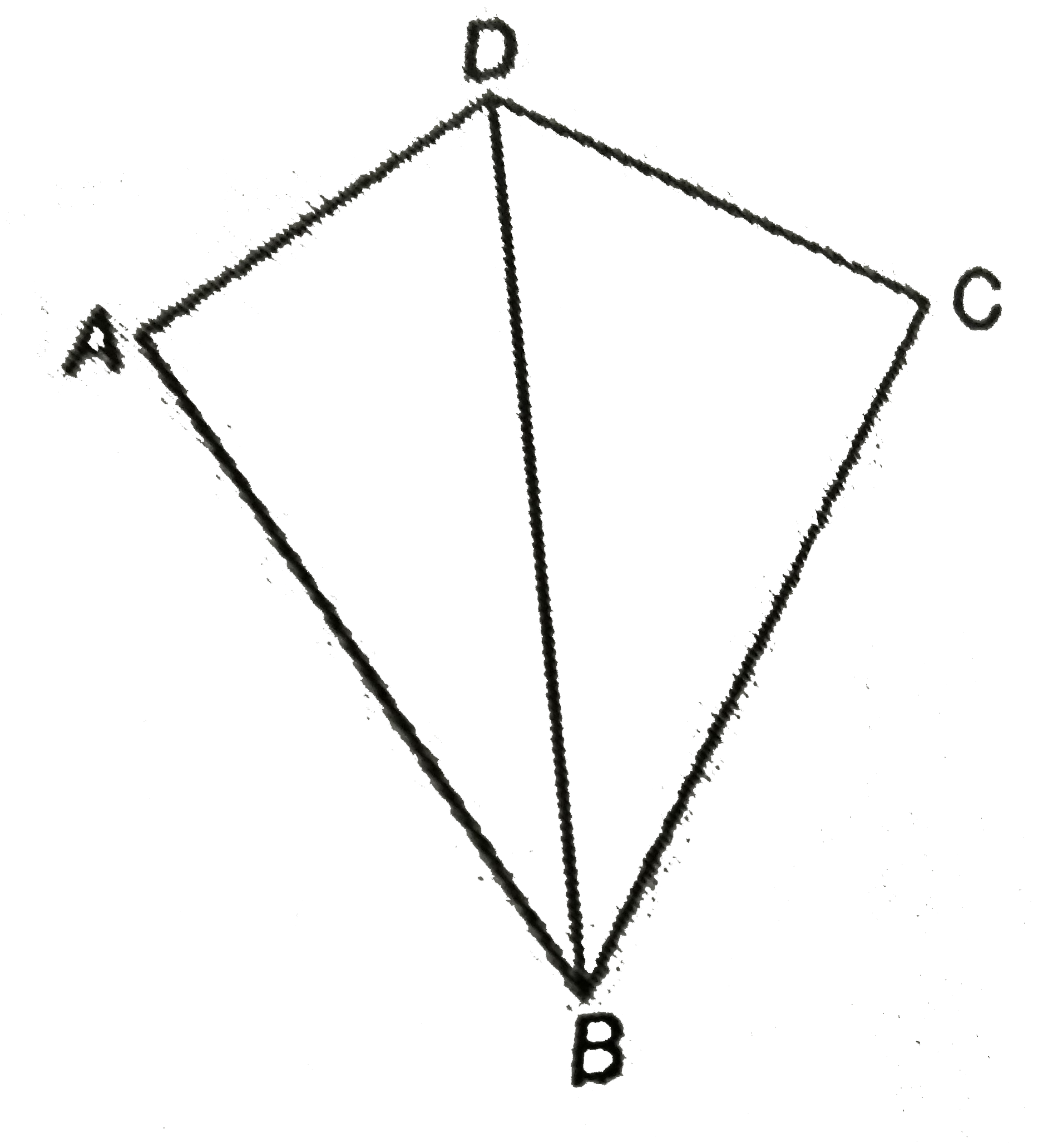
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
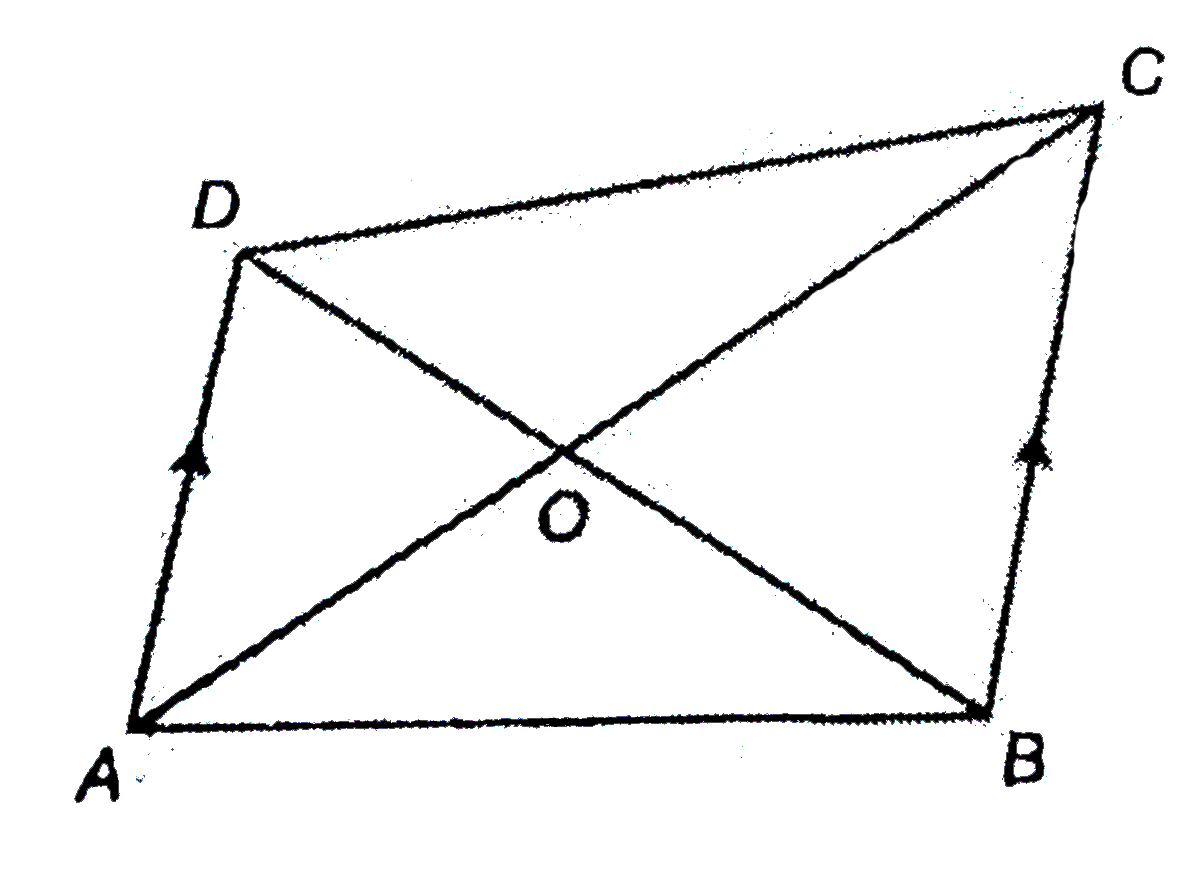
View Solution
