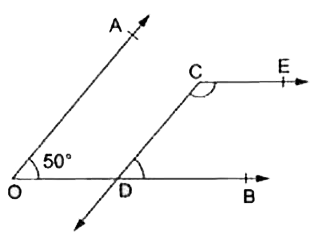
In the adjoining figure it is given that AB||CD,∠ ABO=50∘ and ∠ COD=40∘find the measure of ∠ BOD
To find the measure of ∠BOD given that AB || CD, ∠ABO = 50° and ∠COD = 40°, we can follow these steps:
1. Identify the Given Information:
- We know that lines AB and CD are parallel (AB || CD).
- We are given the angles: ∠ABO = 50° and ∠COD = 40°.
2. Draw a Transversal:
- To analyze the angles formed by the parallel lines, we can draw a transversal line (let's call it line L) that intersects both AB and CD.
3. Use Alternate Angles:
- Since AB is parallel to CD, the angles formed by the transversal line with these parallel lines will have relationships based on the properties of alternate angles.
- Therefore, ∠ABO (50°) is equal to ∠BOE (the angle formed at the transversal with line L) because they are alternate angles.
- So, ∠BOE = 50°.
4. Apply Alternate Angles Again:
- Similarly, since CD is parallel to AB, we can say that ∠COD (40°) is equal to ∠EOD (the angle formed at the transversal with line L).
- Thus, ∠EOD = 40°.
5. Calculate ∠BOD:
- Now, ∠BOD can be found by adding the two angles we just calculated:
- ∠BOD = ∠BOE + ∠EOD
- ∠BOD = 50° + 40° = 90°.
6. Final Answer:
- Therefore, the measure of ∠BOD is 90°.
- We know that lines AB and CD are parallel (AB || CD).
- We are given the angles: ∠ABO = 50° and ∠COD = 40°.
- To analyze the angles formed by the parallel lines, we can draw a transversal line (let's call it line L) that intersects both AB and CD.
- Since AB is parallel to CD, the angles formed by the transversal line with these parallel lines will have relationships based on the properties of alternate angles.
- Therefore, ∠ABO (50°) is equal to ∠BOE (the angle formed at the transversal with line L) because they are alternate angles.
- So, ∠BOE = 50°.
- Similarly, since CD is parallel to AB, we can say that ∠COD (40°) is equal to ∠EOD (the angle formed at the transversal with line L).
- Thus, ∠EOD = 40°.
- Now, ∠BOD can be found by adding the two angles we just calculated:
- ∠BOD = ∠BOE + ∠EOD
- ∠BOD = 50° + 40° = 90°.
- Therefore, the measure of ∠BOD is 90°.
Topper's Solved these Questions
- PROPERTIES OF PARALLEL LINE BOOK - RS AGGARWALCHAPTER - PROPERTIES OF PARALLEL LINE EXERCISE - EXERCISE 14
15 Videos
- PROFIT AND LOSSBOOK - RS AGGARWALCHAPTER - PROFIT AND LOSSEXERCISE - Test paper
9 Videos
- PROPERTIES OF TRIANGLESBOOK - RS AGGARWALCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - EXERCISE 15-D
18 Videos
Similar Questions
Knowledge Check
In the adjoining figure it is given that AB∣∣CD,∠BOC=108∘ and ∠OCA=120∘ Find ∠AOC,
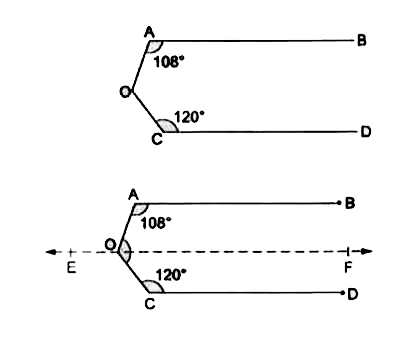 A∠AOC=140∘B∠AOC=135∘C∠AOC=130∘D∠AOC=132∘
A∠AOC=140∘B∠AOC=135∘C∠AOC=130∘D∠AOC=132∘
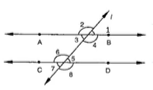
In Figure, given that AB∣∣CD. If ∠1=(120−x)0and ∠5=5x0, find the measures of ∠1 and ∠5.
View SolutionIn the adjoining figure,AB=AC.Find the value of x
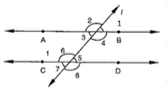
View SolutionIn Figure, given that AB∣∣CD If ∠4=(x+20)0and ∠5=(x+8)0, find the measures of ∠4 and ∠5
View SolutionIn the adjoining figure AB||CD .Find the value of x
View SolutionIn given figure, show that AB || CD
View SolutionIn the given figure find z if AB=CD
View SolutionIn the adjoining figure, AB||CD. If the ∠BAE=25∘and∠CDE=30∘, then find ∠AED
View Solution