In the adjoining figure, M is the midpoint of seg AB and seg CM is a median of ΔABC. Find A(ΔAMC)A(ΔBMC).
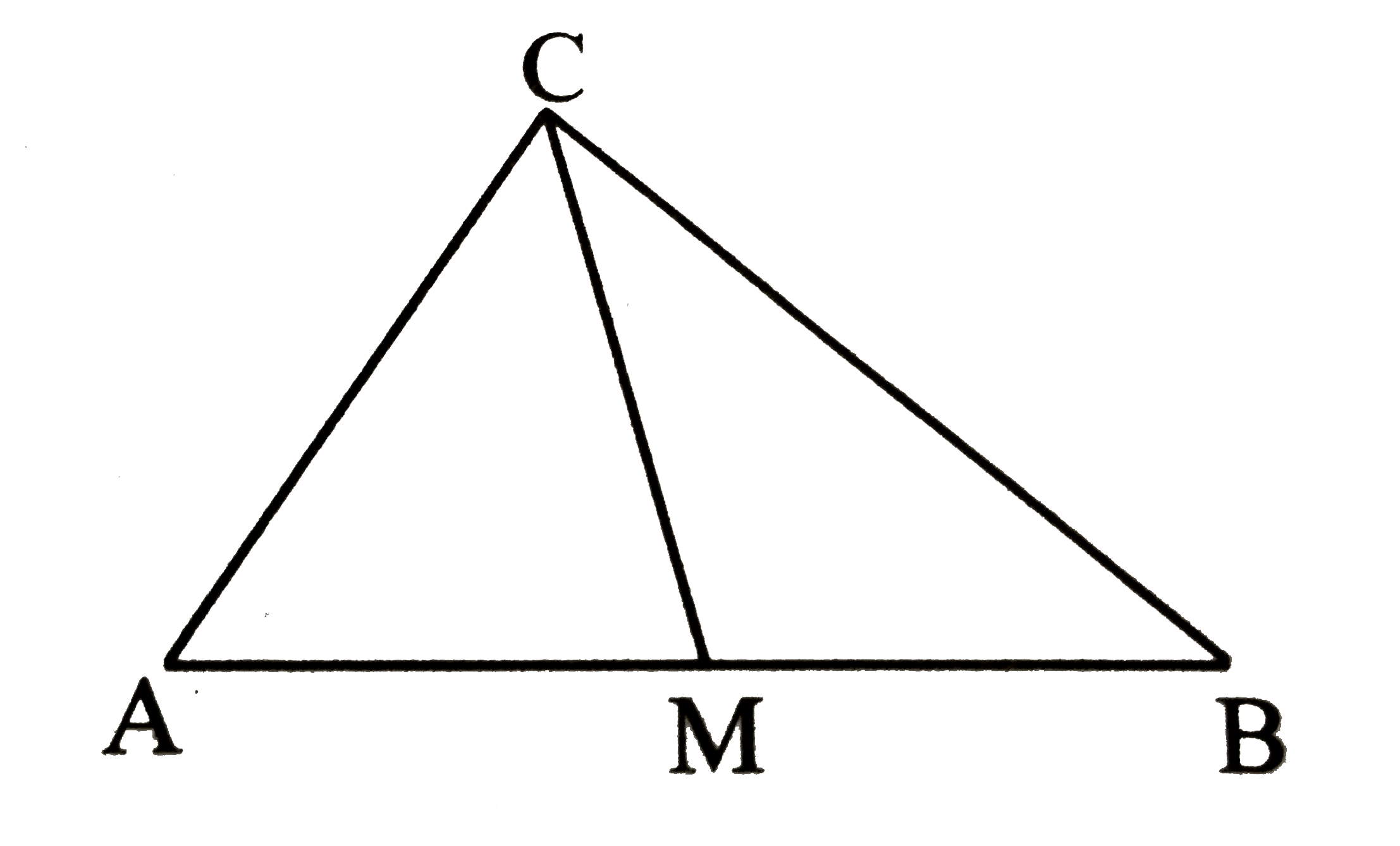
The correct Answer is:∴A(ΔAMC)A(ΔBMC)=1
Step by step video & image solution for In the adjoining figure, M is the midpoint of seg AB and seg CM is a median of DeltaABC. Find (A(DeltaAMC))/(A(DeltaBMC)). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Textual Activity4videos
SIMILARITY
- BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Try this1videos
SIMILARITY
- BOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics14videos
QUESTION FROM STD. IX
- BOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-621videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the adjoining figure D is the midpoint of BC of a ΔABC,DMandDN are the perpendiculars on AB and AC respectively and DM=DN, then the ΔABC is :
 Aright angledBisoscelesCequilateralDscalene
Aright angledBisoscelesCequilateralDscalene
.Point M is the midpoint of Seg AB.If AB=8 then find the length of AM.
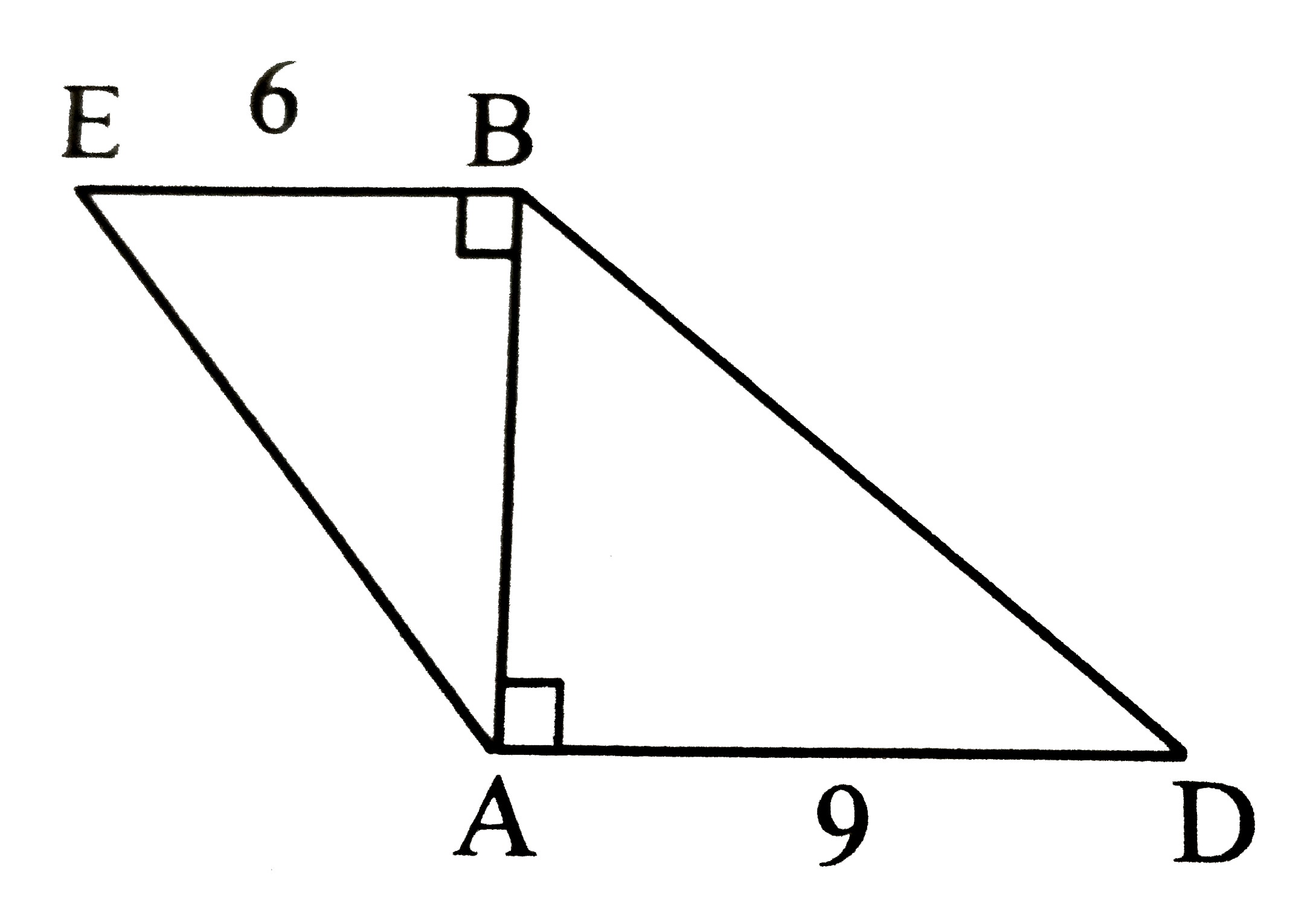
View SolutionIn the given figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and AD = 9, then find A(ΔABE)A(ΔBAD).
 View Solution
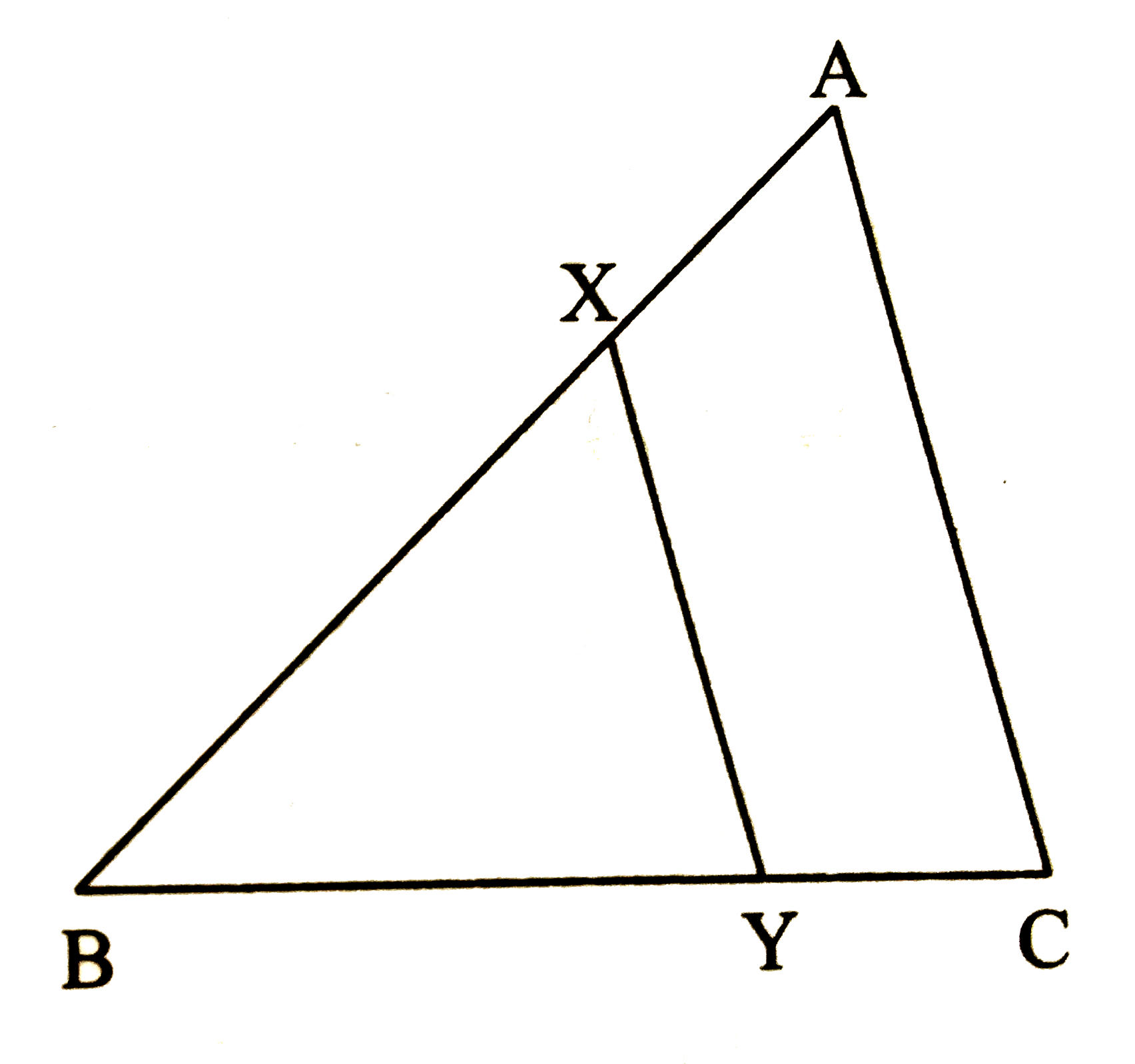
View SolutionIn the adjoining figure, seg XY∣∣ seg AC, IF 3AX=2BX and XY=9 then find the length of AC.
 View Solution
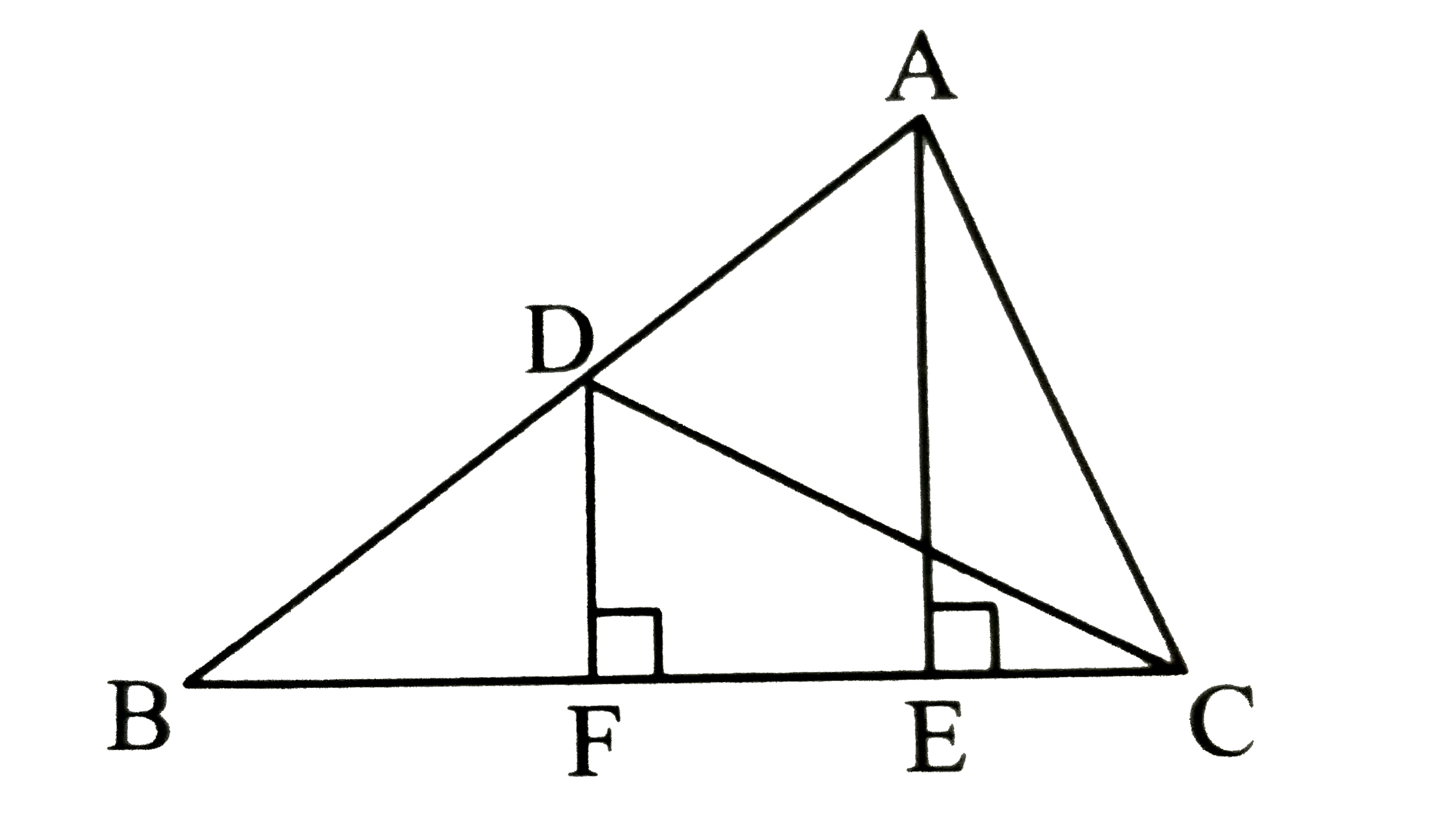
View SolutionIn given figure, seg AE ⊥ seg BC, seg DF ⊥ line BC,
AE = 4, DF = 6, then find A(ΔABC)A(ΔDBC).
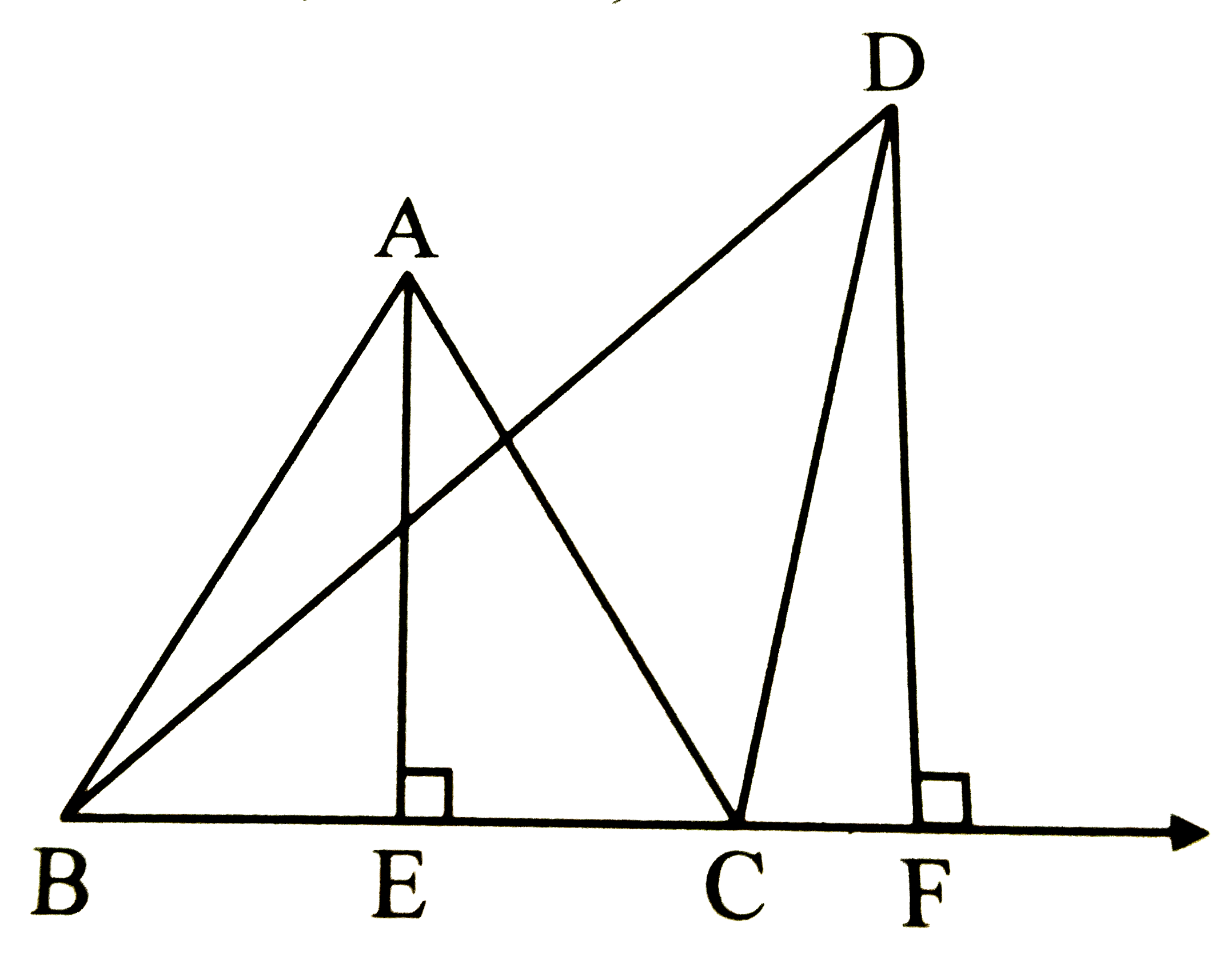 View Solution
View Solutionpoint C is the midpoint of seg AB. If AC = 5.5, then find the length of AB.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
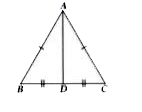 Prove that:
Prove that:
ΔADB≅ΔADCView SolutionIn the adoining figure, XY || seg AC. If 2 AX = 3 BX and XY = 9, find the value of AC.
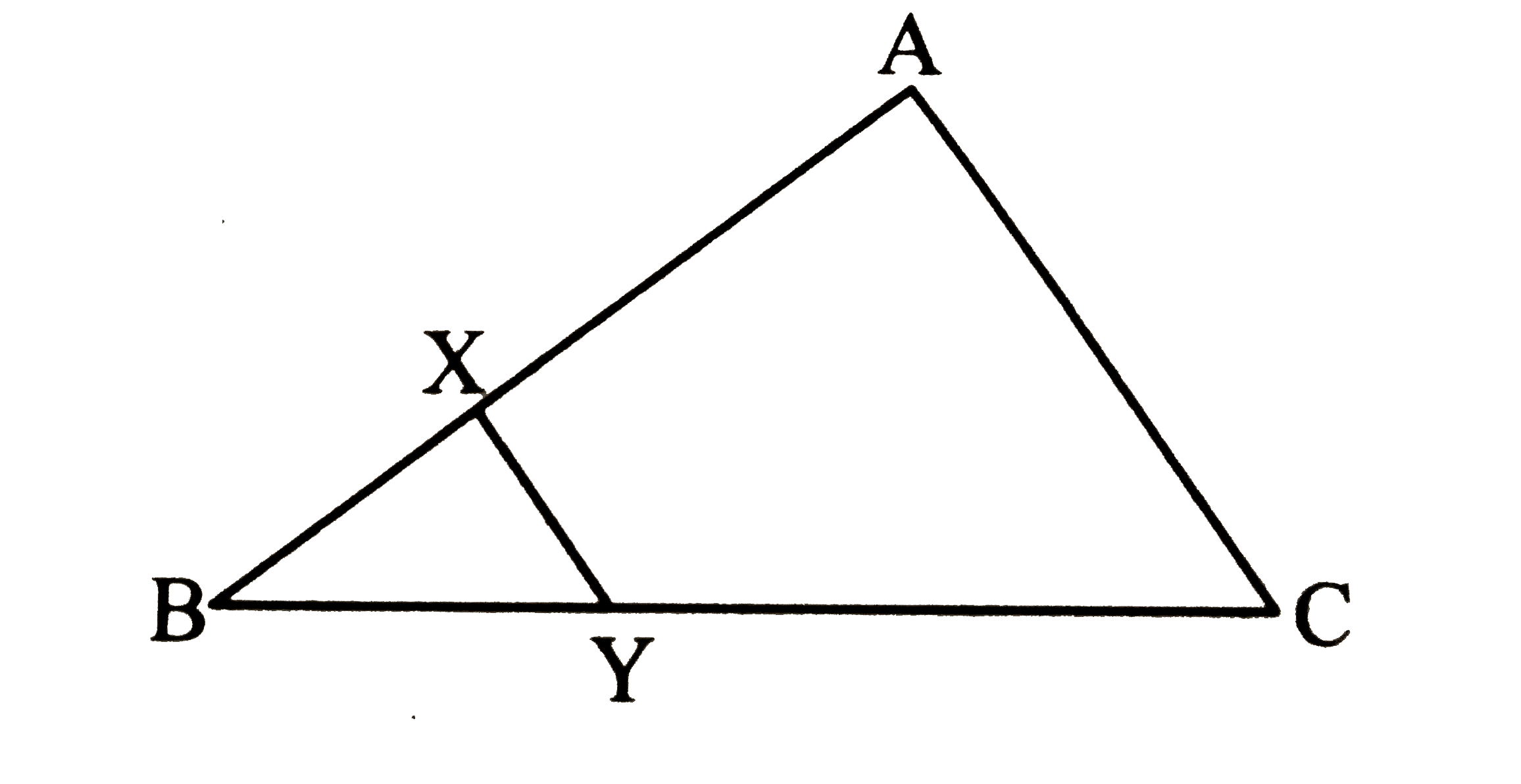 View Solution
View Solution