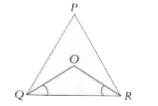
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If XS⊥PQ. Prove that :
(i) ΔXTQ≅ΔXSQ
(ii) PX bisects angle P.

Step by step video & image solution for In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If XS bot PQ. Prove that : (i) DeltaXTQ cong DeltaXSQ (ii) PX bisects angle P. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7b
15 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
Knowledge Check
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If XS⊥PQ. Prove that :
(i) ΔXTQ≅ΔXSQ
(ii) PX bisects angle P.
 ASASBRHSCAASDASA
ASASBRHSCAASDASAIn the figure below 2∠P=∠QOP, OQ and OR are bisectors of ∠Qand∠R respectively. Find ∠P
 A60∘B70∘C40∘D80∘
A60∘B70∘C40∘D80∘A triangle ABC is inscribed in a circle and the bisectors of the angles A, B and C meet the cir cumference at P, Q and R respec tively. The angles of the triangle PQR respectively are
A90∘−A2,90∘+A290∘+C2B90∘+A2,90∘−B2,90∘−CC90∘−A2,90∘−B2,90∘−C2DNone of these
If the vertices P, Q and R of a triangle have coordinates (2,3,5),(−1,3,2) and (3,5,−2) respectively, then find the angles of the triangle PQR.
View SolutionIf the vertices P, Q and R of a triangle have coordinates (2,3,5),(−1,3,2) and (3,5,−2) respectively, then find the angles of the triangle PQR.
View SolutionABC is a cyclic triangle and the bisectors of ∠BAC,∠ABCand∠BCA meet the circle at P,Q and R respectively. Then the angle ∠RQP is:
View SolutionABC is a cyclic triangle and the bisectors of ∠BAC,∠ABCand∠BCA meet the circle at P,Q and R respectively. Then the angle ∠RQP is:
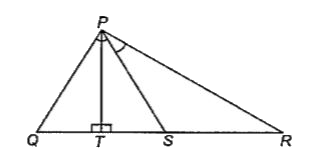
View SolutionIn Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
View Solution