In the adjoining figure, seg AB and seg AD are chords of the circle . C is a point on tangent to the circle at point A. IF m(arc APB)=80∘and ∠BAD=30∘, then find
(i) ∠BAC (ii) m(arc BQD)
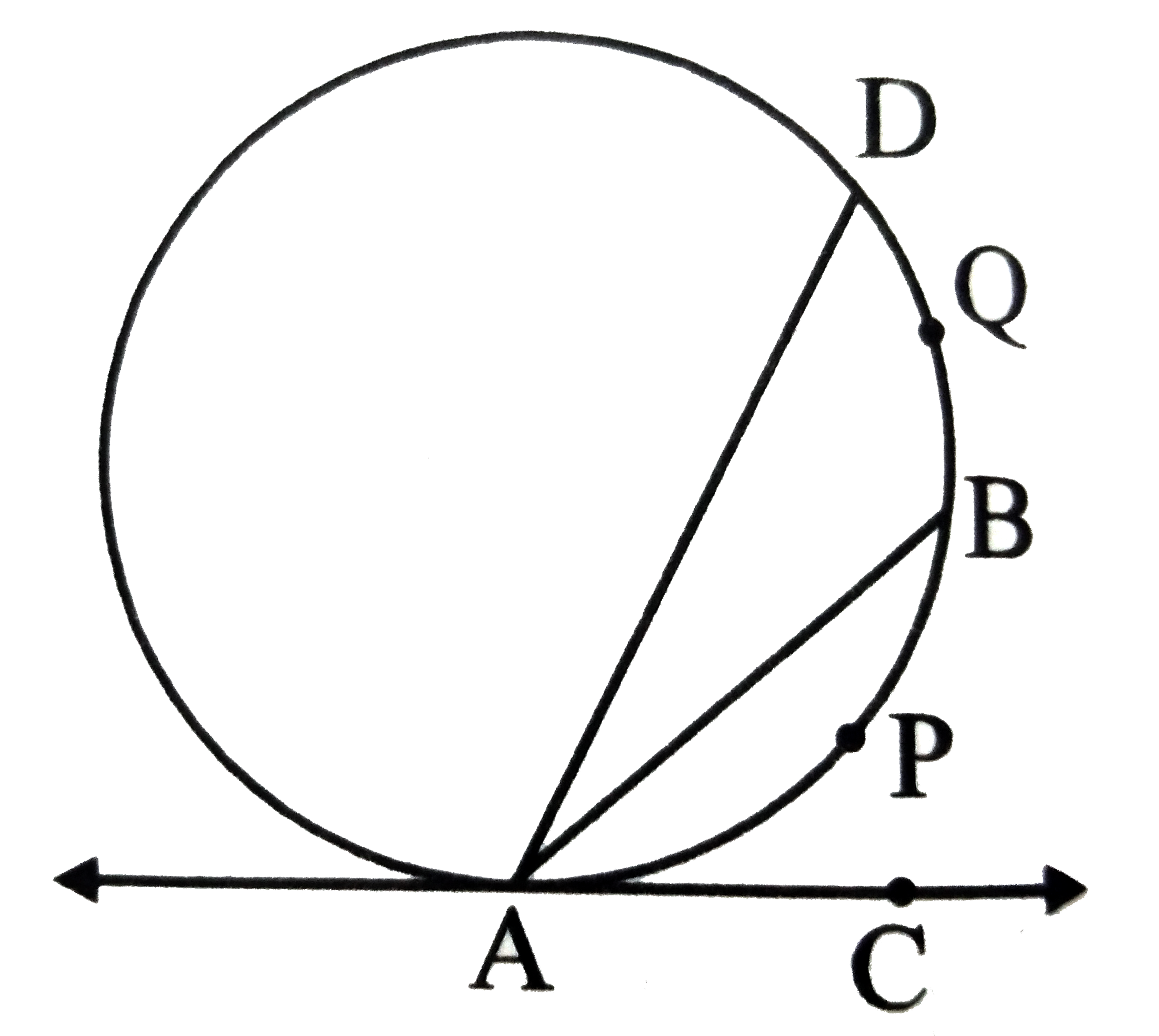
The correct Answer is:40∘,60∘
Step by step video & image solution for In the adjoining figure, seg AB and seg AD are chords of the circle . C is a point on tangent to the circle at point A. IF m(arc APB)=80^@and angleBAD=30^@, then find (i) angleBAC (ii) m(arc BQD) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Chapter Assessment9videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Multiple Choice Question25videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics4videos
CHALLENGING QUESTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT19videos
CO-ORDINATE GEOMETRY
Similar Questions
In the adjoining figure, O is the centre of the circle. AB is an arc of the circle and ∠AOB=80∘. Find ∠ACB.
 View Solution
View SolutionIn the following figure, AB is an arc of the circle, C and D are the points on the circle. If ∠ACB=30∘, Find ∠ADB.
 View Solution
View SolutionIn the following figure, O is the centre of the circle. AB is an arc of the circle, such that ∠AOB=80∘.Find ∠ACB.
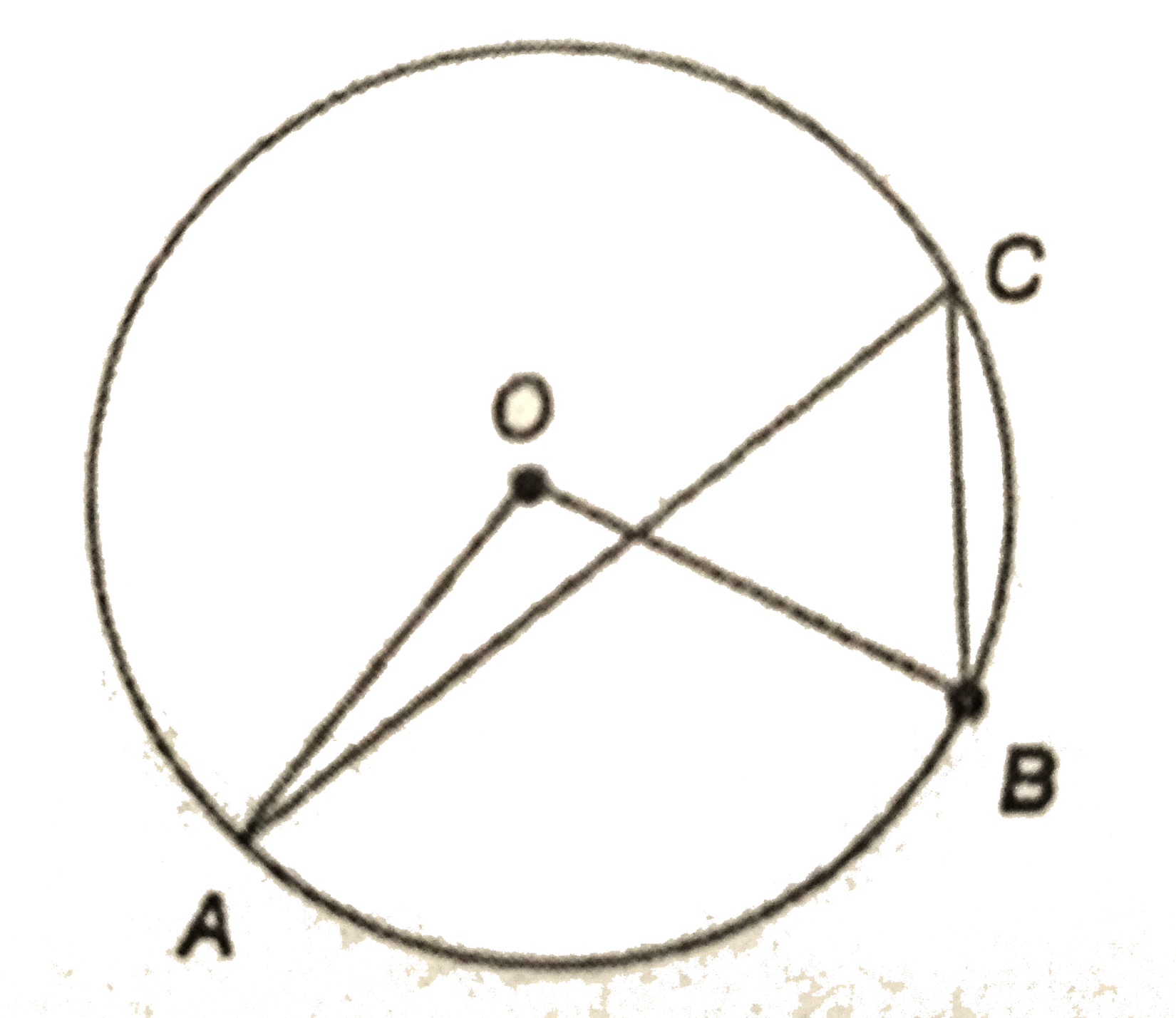 View Solution
View SolutionIn the adjoining figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠RTS is an acute angle.
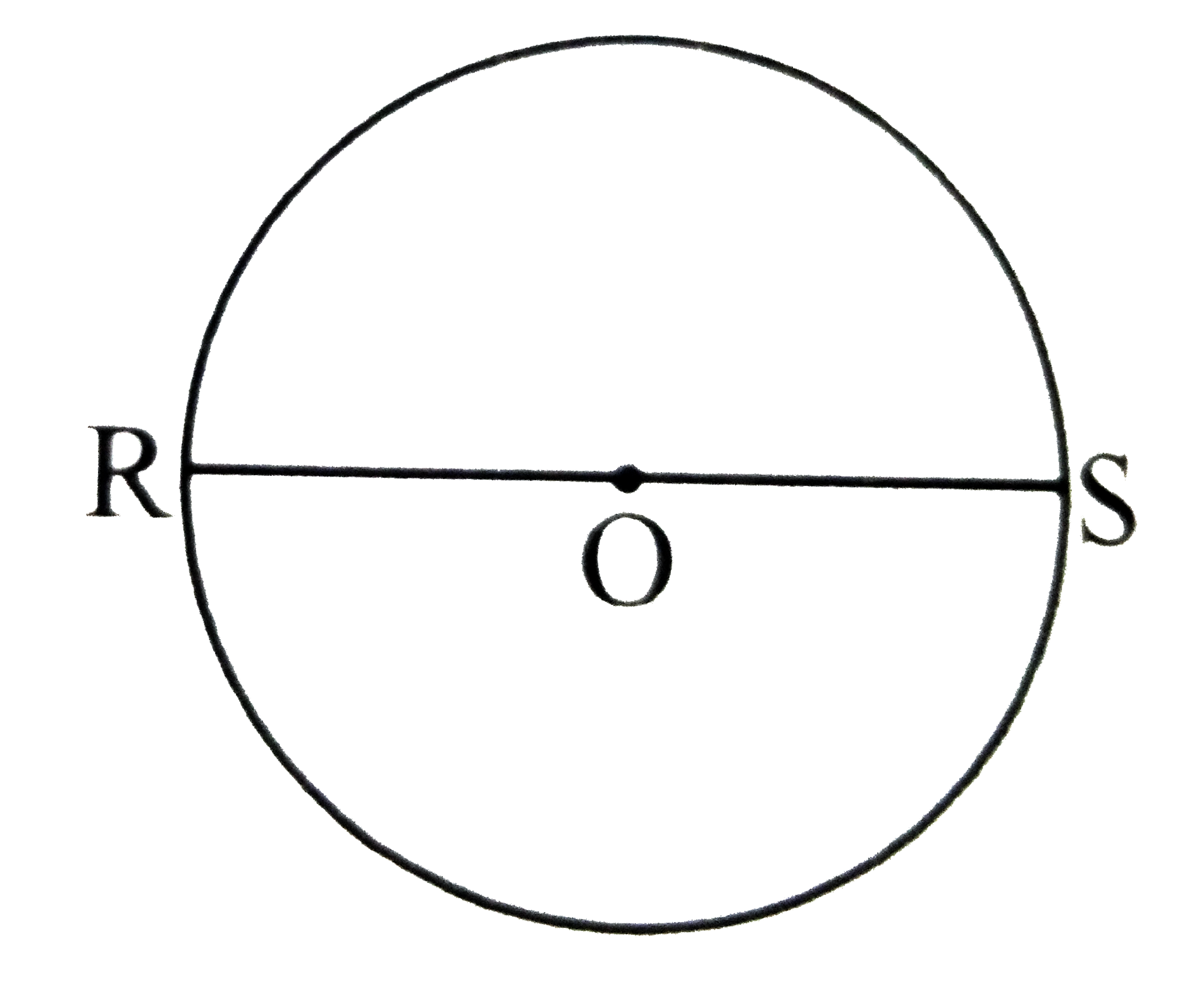 View Solution
View SolutionIn the adjoining figure, P is the circumcentre of the ΔABC.m∠APC=118∘ and m∠PBC=45∘ , then find:
(i) m(arc BXC)
(ii) m(arc BCA)
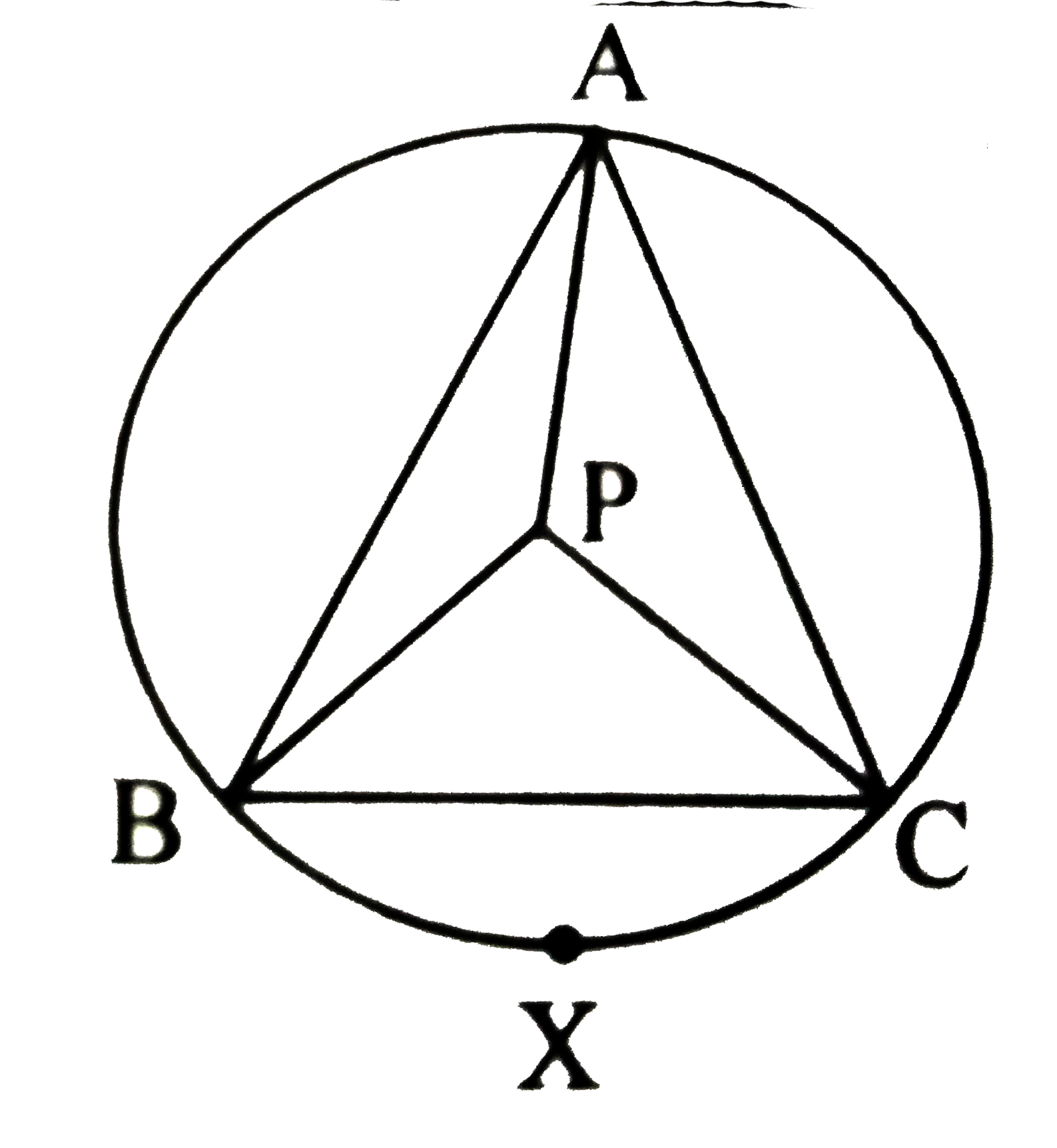 View Solution
View SolutionIn the given figure , O is the centre of the circle. If m(arc AXB)=80∘, then m∠AOB=
 View Solution
View SolutionIn the figure, chord AB∣∣ tangent DE. Tangent DE touches the circle at point C then prove AC = BC.
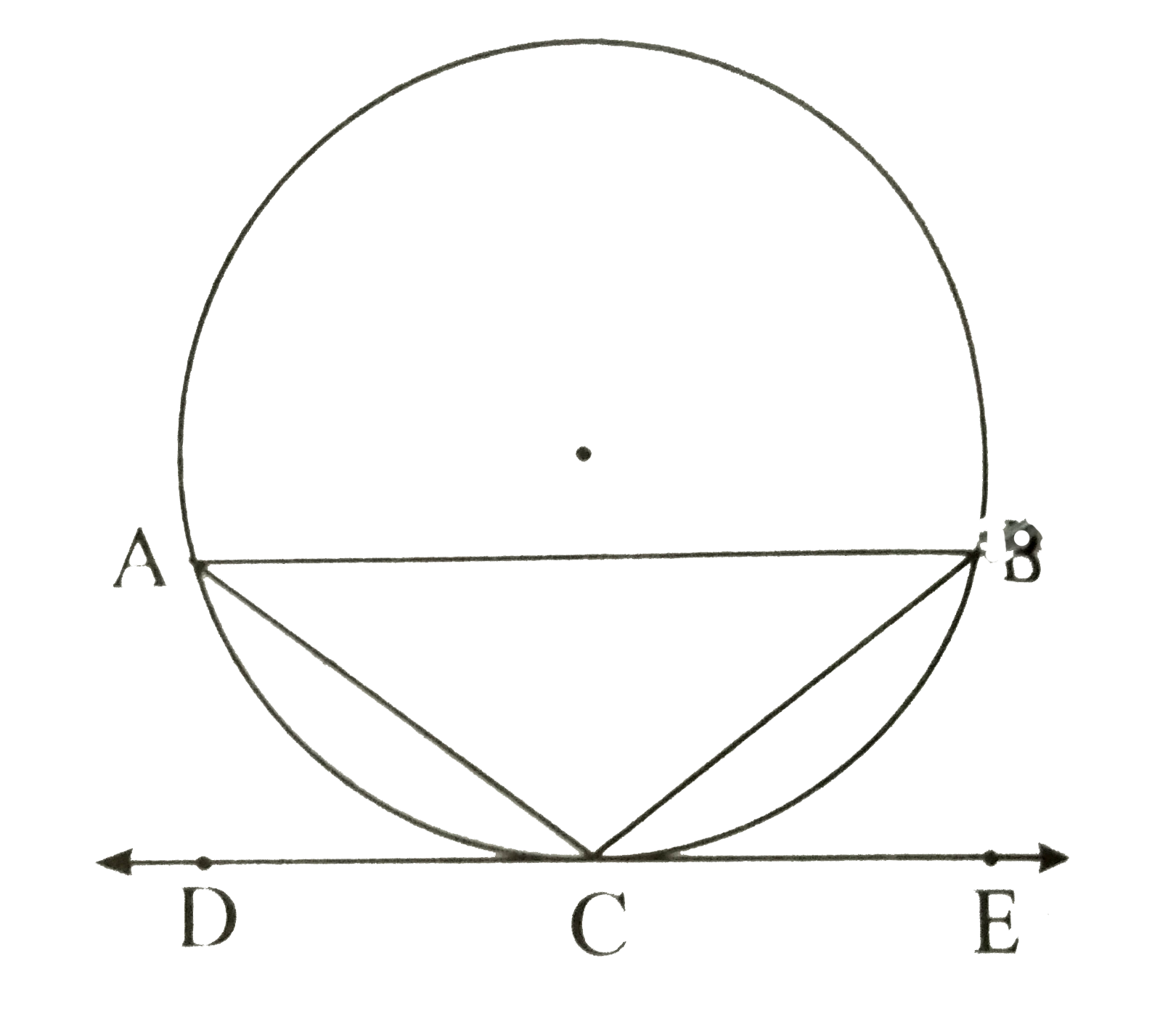 View Solution
View SolutionIn the figure , seg AB is the chord of the circle with centre O. if AM =4 cm then find MB and AB. State your reason.
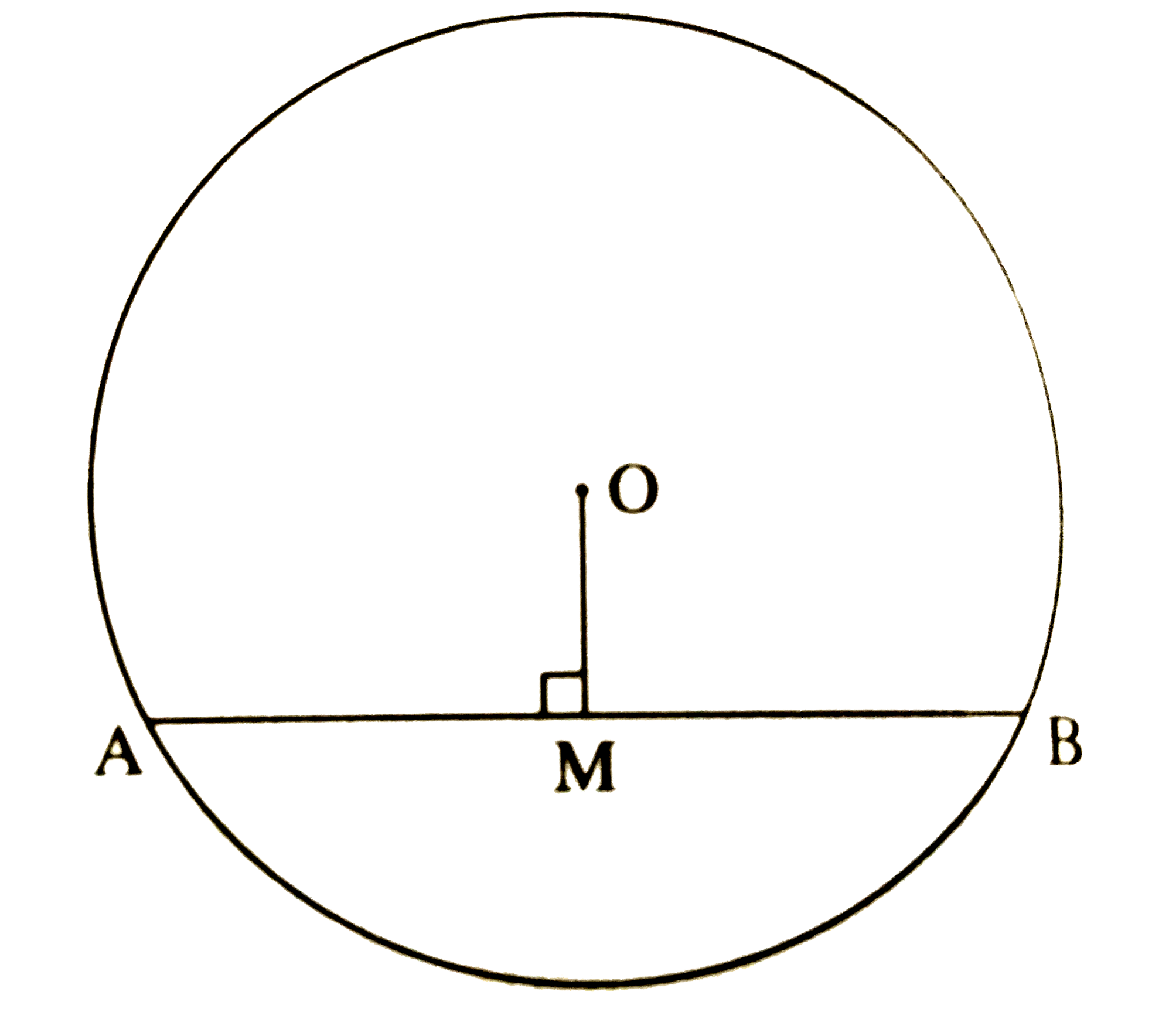 View Solution
View SolutionIn the adjoining figure, O is the centre and seg AB is a diameter. At the point C on the circle, the tangent CD is drawn. Line BD is a tangent to the circle at the point B. Show that segOD ∣∣ chord AC.
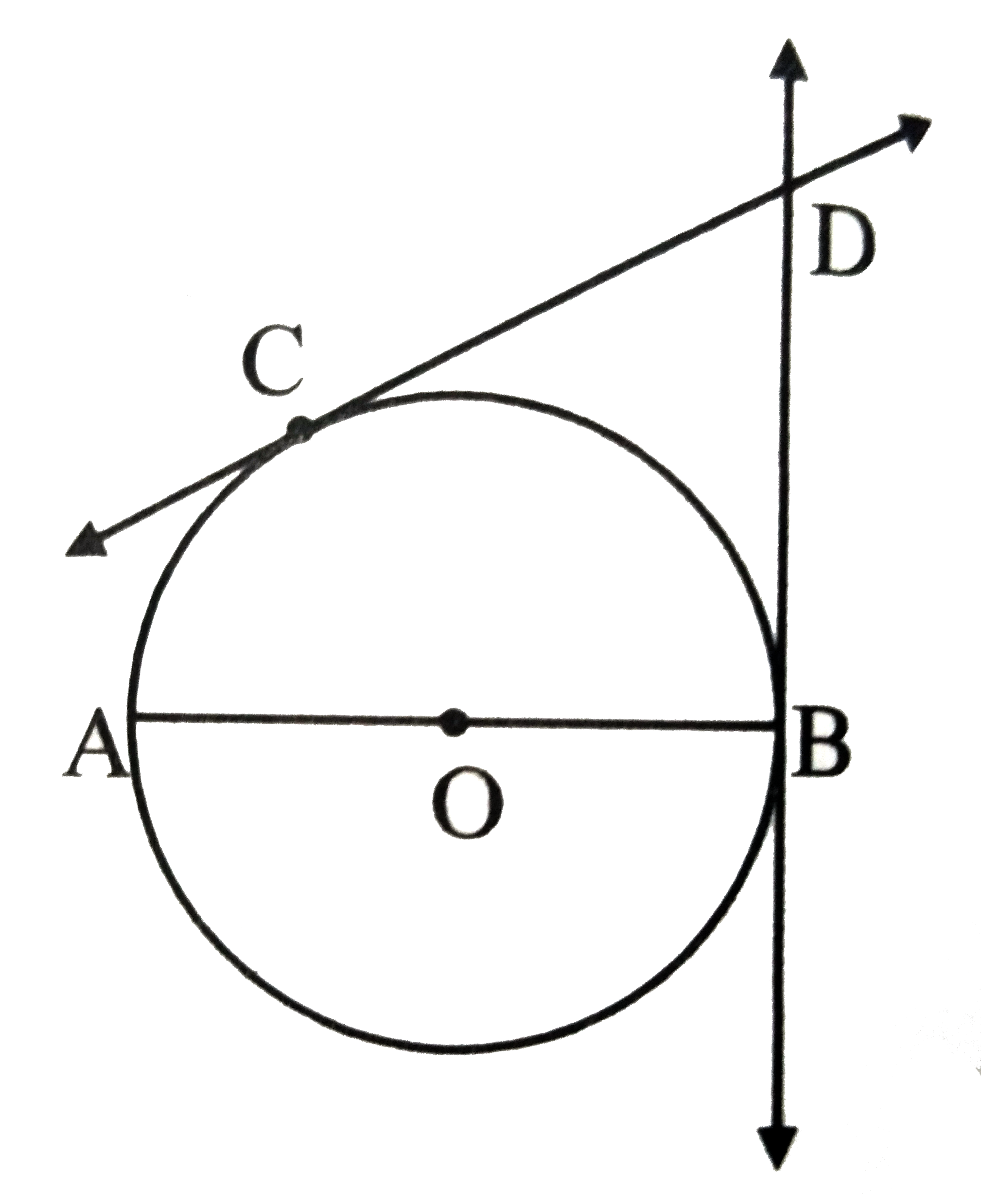 View Solution
View SolutionChords AB and CD of a circle intersect in point Q in interior of a circle. If m(arc AD)=25∘ and m(arc BC)=31∘, find ∠BQC.
 View Solution
View Solution

