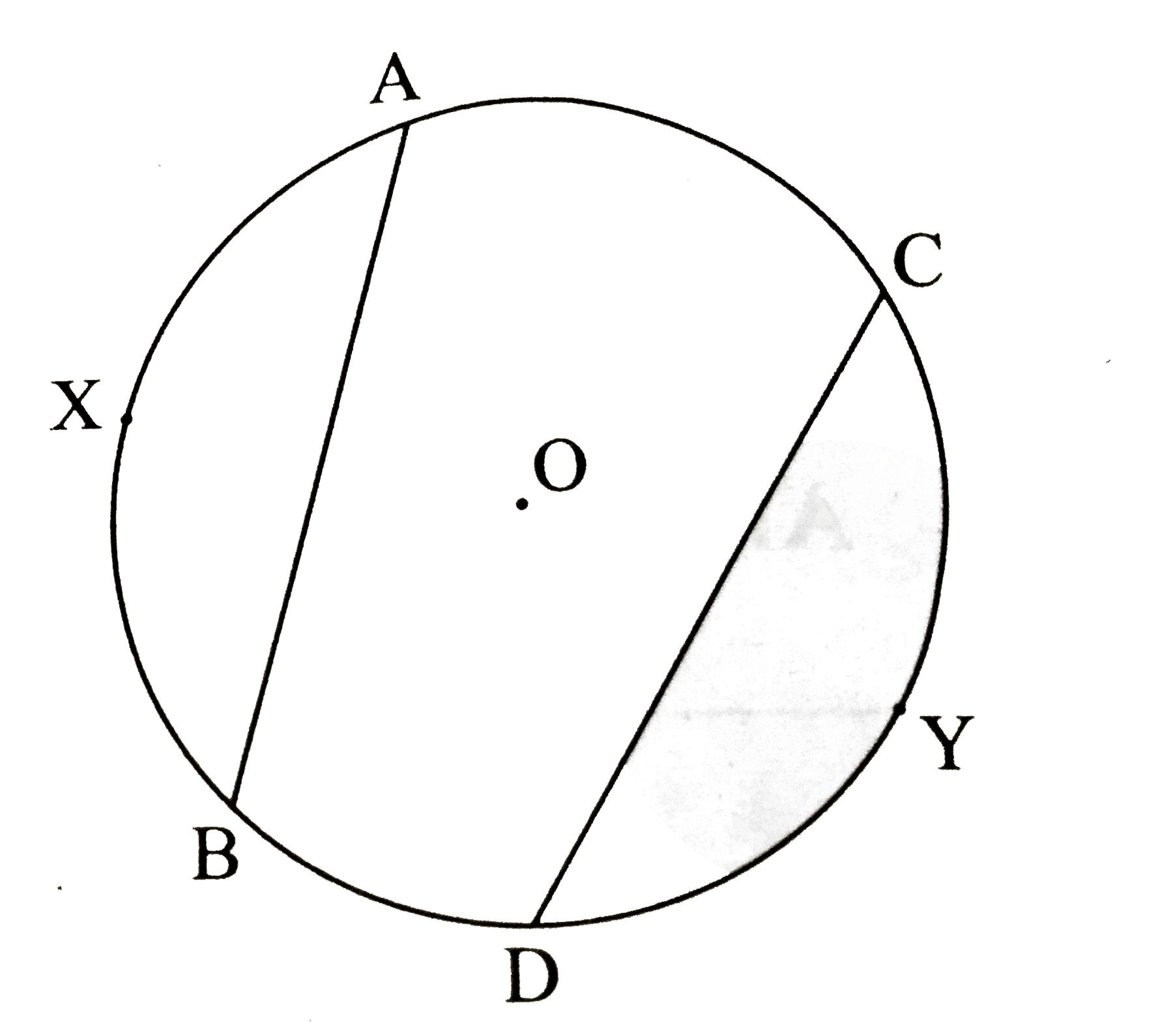
Chords AB and CD of a circle intersect in point Q in interior of a circle. If m(arc AD)=25∘ and m(arc BC)=31∘, find ∠BQC.

The correct Answer is:∠BQC=28∘
Step by step video & image solution for Chords AB and CD of a circle intersect in point Q in interior of a circle. If m(arc AD)=25^(@) and m(arc BC)=31^(@), find /_BQC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.1
9 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.2
8 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.5
8 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
Knowledge Check
Two chords AB and CD of a circle with centre O intersect at point P within the circle. ∠AOC+∠BOD=?
A∠APCB2∠APCC32∠APCDNone of theseChords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm, AP = 4 cm and PC = 5 cm, then CD is equal to:
A4.8 cmB6.8 cmC9.8 cmD7.8 cm
In the adjoining figure, seg AB and seg AD are chords of the circle . C is a point on tangent to the circle at point A. IF m(arc APB)=80∘and ∠BAD=30∘, then find
(i) ∠BAC (ii) m(arc BQD)
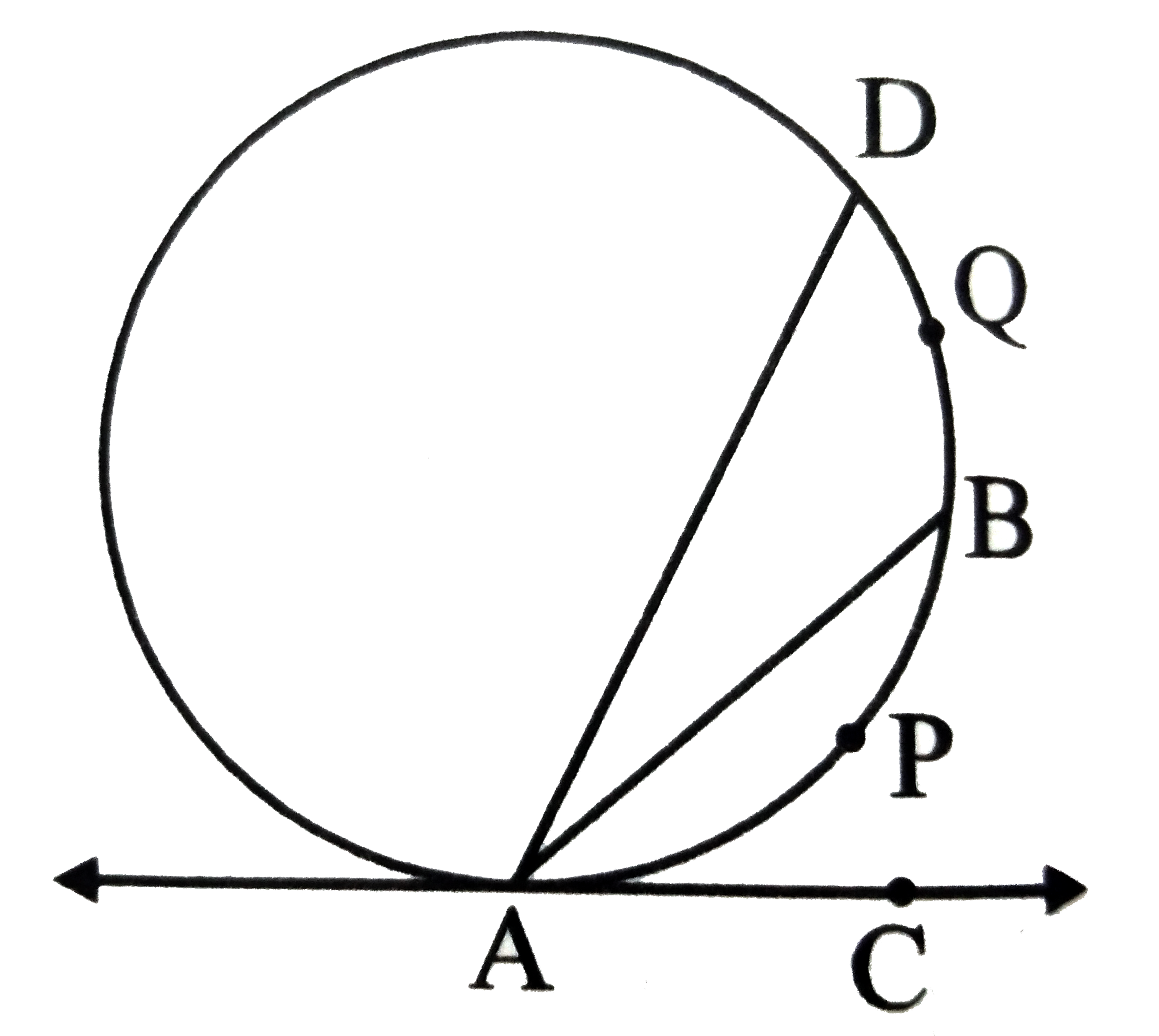
View SolutionTwo chords AB and CD of a circle intersect at a point outside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
View SolutionTwo chords AB and CD of a circle intersect at A, AB is the diameter and CD is ⊥ to AB .AE = 2 cm AB = 10 cm,Find value of ED.
View SolutionIf two chords AB and CD of a circle AYDZBWCX intersect at right angles, then prove that arc CXA+arc DZB=arc AYD+arc BWC =semi-circle.

View SolutionIn the figure , ∠QPR has its vertex outside the circle such that m ( arc QR ) = 200∘ and m ( arc ST ) =90∘, then ∠QPR= ?

View SolutionIn the figure, ∠QPR has its vertex outside the circle such that m(arc QR)=200∘ and m(arc ST)=90∘, then ∠QPR=………

View Solution