In the adjoining figure,OD is perpendicular to the chord AB of a circle what centre O. If BC is a diameter, show that AC∣∣DO and AC=2×OD.
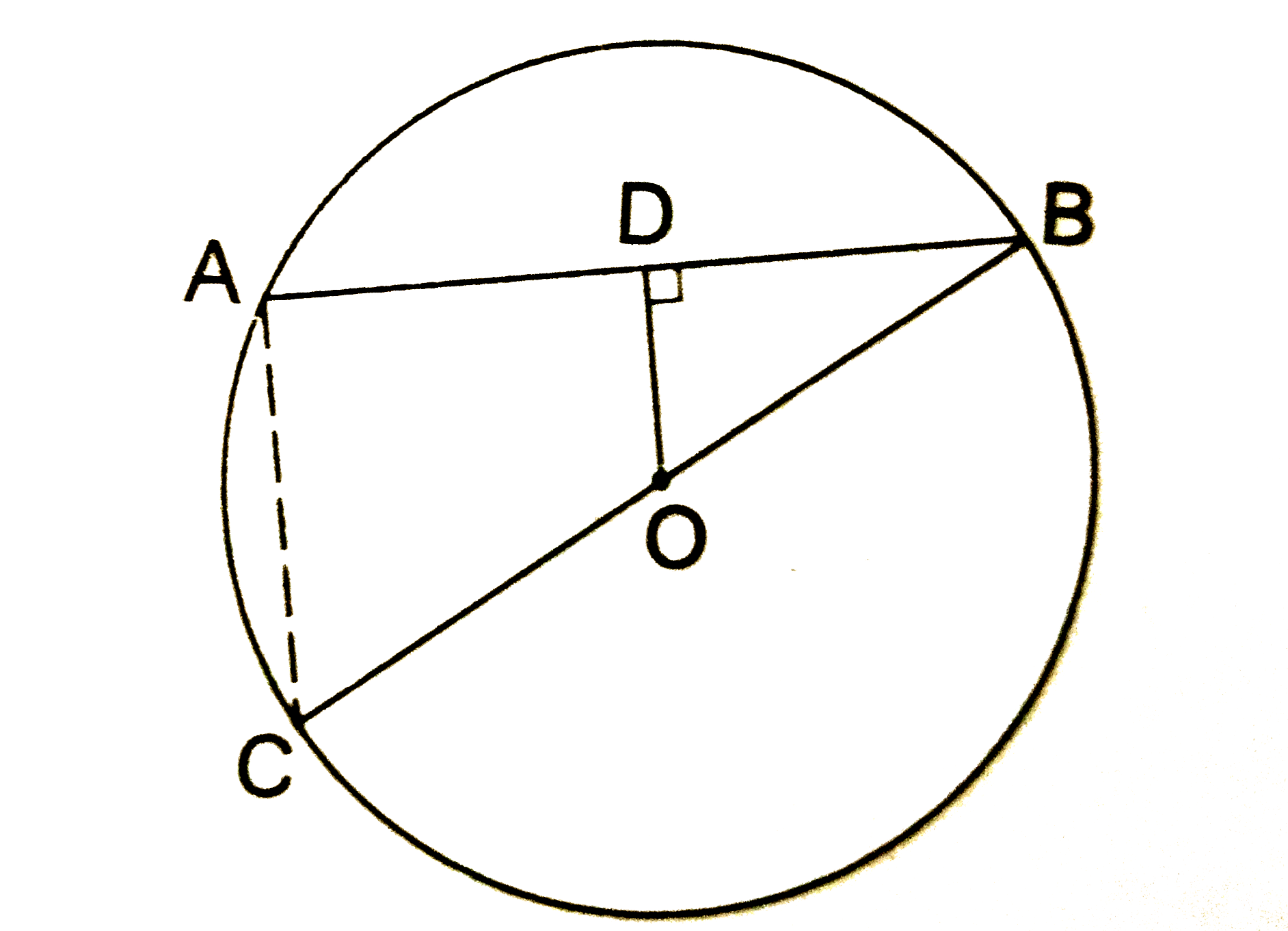
OD ⊥ AB⇒ D is the midpoint f AB.
Also , O is the midpoint of BC. Join AC.
Now ,in ΔABC, D is the midpoint of AB and O is the midpoint of BC.
∴DO∣∣AC and DO=12AC.
Similar Questions
In the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD
View SolutionIn the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIn a circle OD is perpendicular to chord AB of a circle with centre O. If BC is a diameter then the AC/OD is:
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.

View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
View SolutionIn the adjoining figure, DE is a chord parallel to diameter AC to the circle with centre. O if ∠CBD=60∘. Calculate ∠CDE.

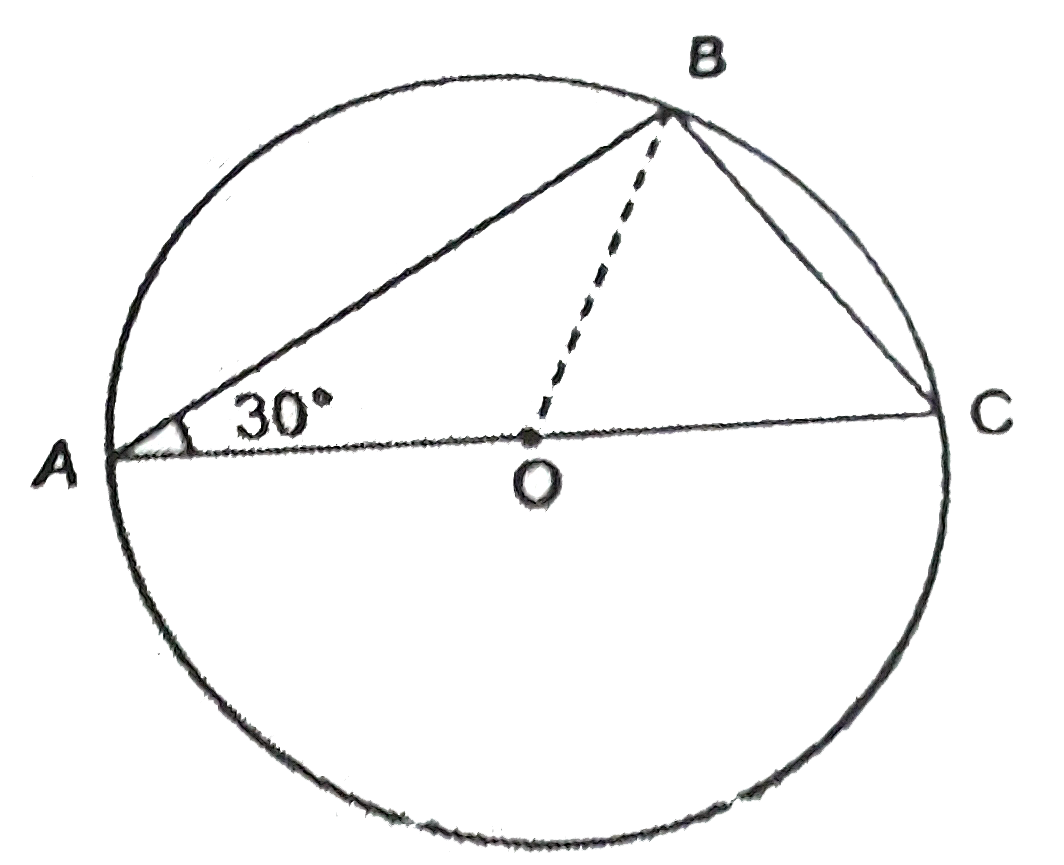
View SolutionIn the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
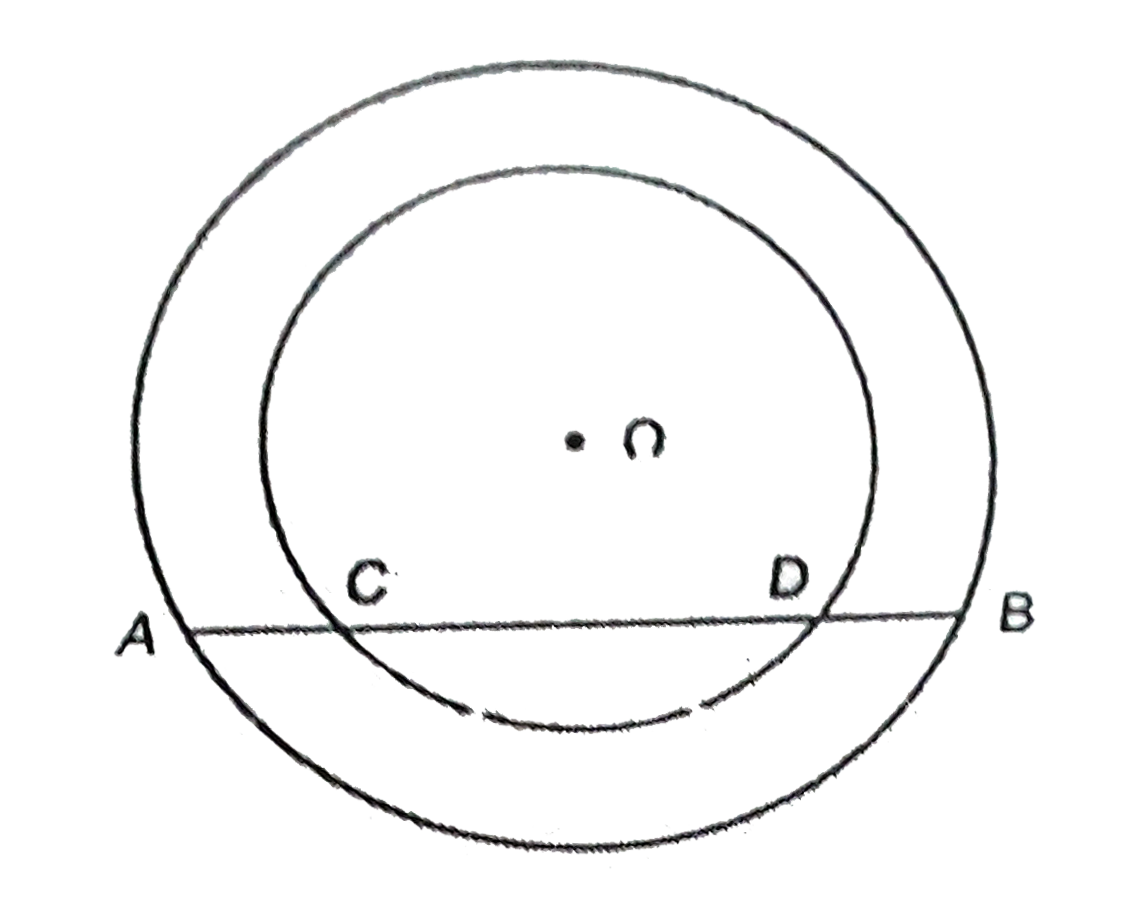
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

View Solution
