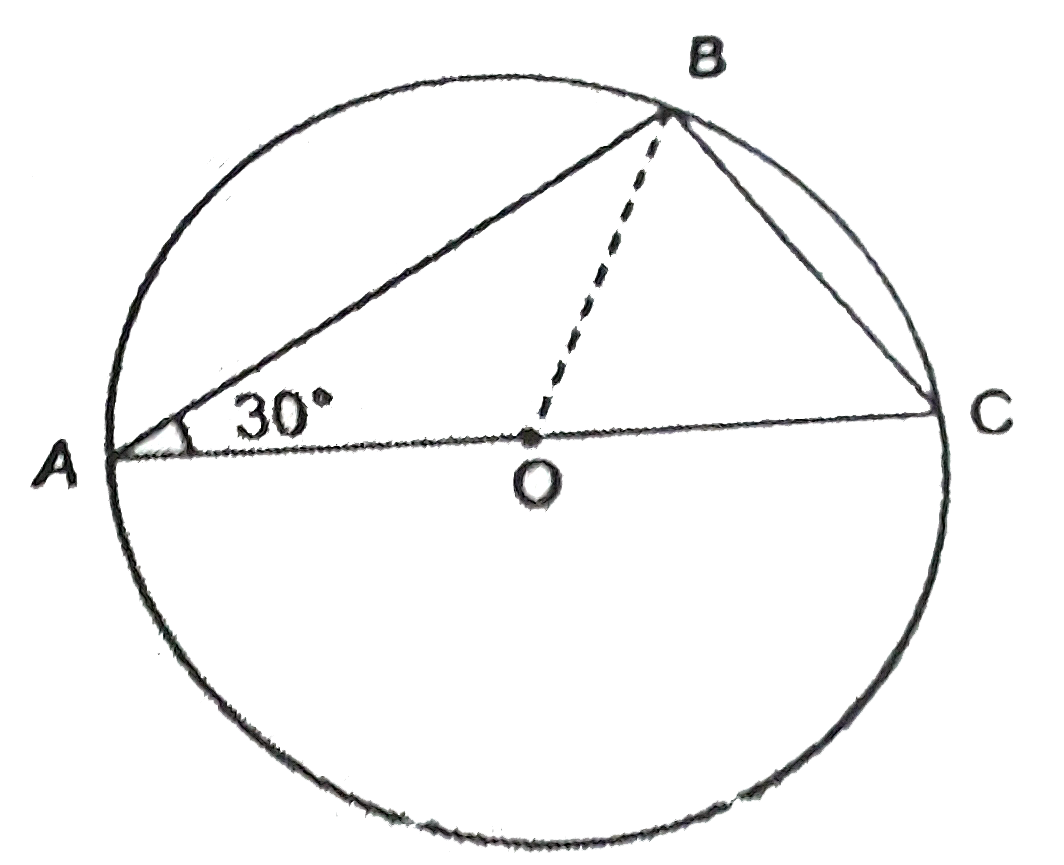
In the adjoining figure, is the centre of a circle in which AB and CD are two diameters. Prove that and . If , then find the value of .

The correct Answer is:
NA
Topper's Solved these Questions
- CIRCLE Book:NAGEEN PRAKASHANChapter:CIRCLE Exercise:Revision Exercise (very Short Answer Question)
Explore 10 Videos
- CIRCLE Book:NAGEEN PRAKASHANChapter:CIRCLE Exercise:Revision Exercise (short Answer Questions )
Explore 10 Videos
- CIRCLE Book:NAGEEN PRAKASHANChapter:CIRCLE Exercise:Exercise 10b
Explore 19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHANChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (long Answer Question)
Explore 5 Videos
- CO-ORDINATE GEOMETRY Book:NAGEEN PRAKASHANChapter:CO-ORDINATE GEOMETRY Exercise:Exercise
Explore 8 Videos
Similar Questions
Knowledge Check
In the adjoining figure, O is the centre of the circle and D ∠OBD=50∘. Find the ∠BAD :
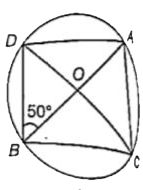 A60∘B40∘C80∘D45∘
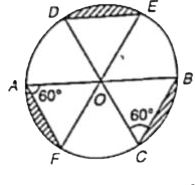
A60∘B40∘C80∘D45∘In the adjoining figure O is the centre of the circle with radius r’ AB, CD and EF are the diameters of the circle. ∠OAF=∠OCB=60∘ . What is the area of the shaded region?
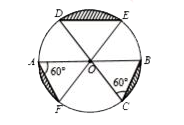 Ar22(π−3√32)Br22(π−3√34)Cr23(π−2√33)DData insuffincient
Ar22(π−3√32)Br22(π−3√34)Cr23(π−2√33)DData insuffincient
In the adjoining figure, O is the centre of the circle. AB and CD are equal chords.
If ∠AOB=100∘, then find ∠CED.
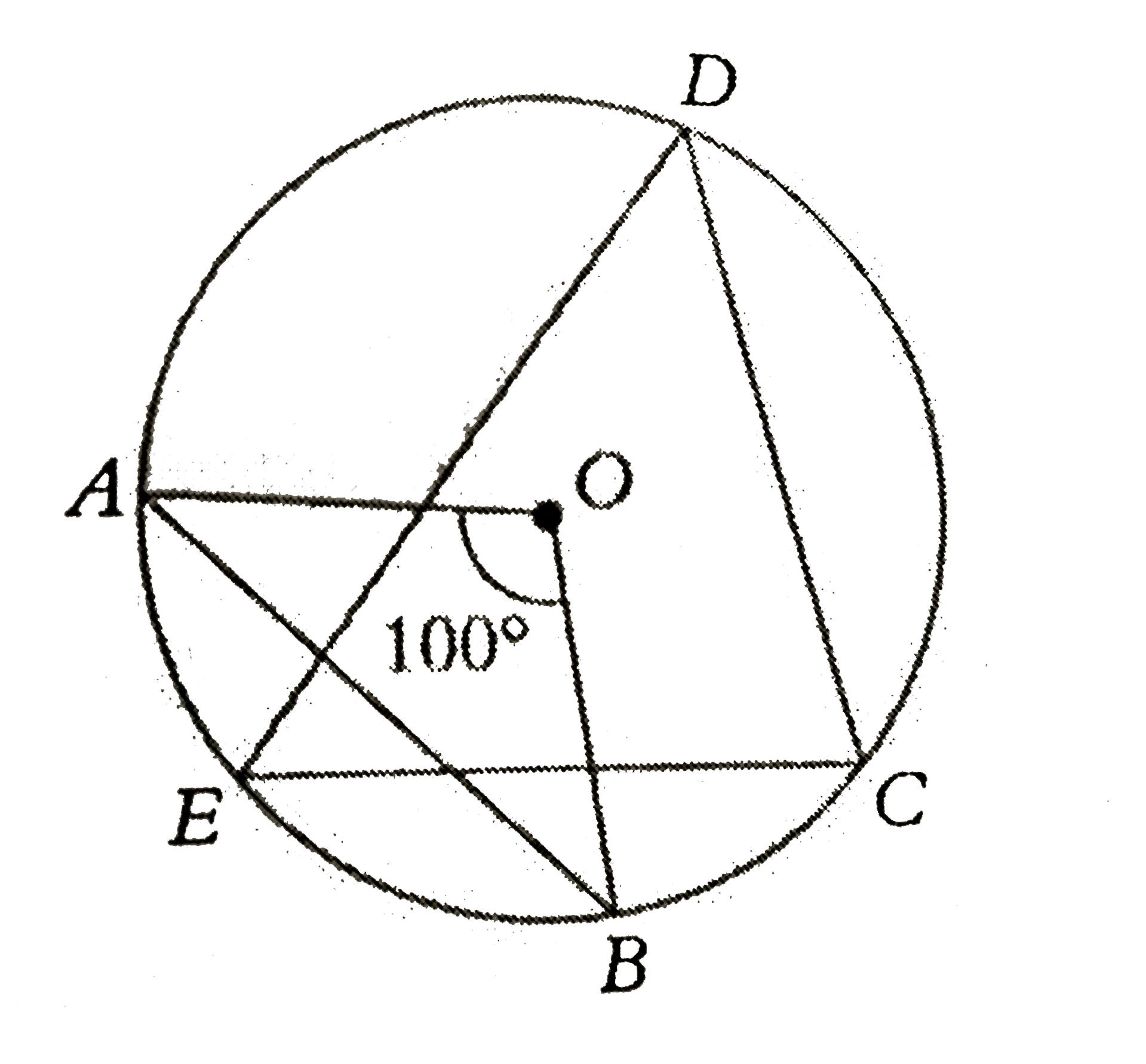
View SolutionIn the adjoining figure O is the centre of the circle with radius 'r' AB, CD and EF are the diameters of the circle. ∠OAF=∠OCB=60∘. What is the area of the shaded region?
View SolutionIf figure, O is the centre of the circle, BD=ODandCD⊥AB. Find∠CAB.

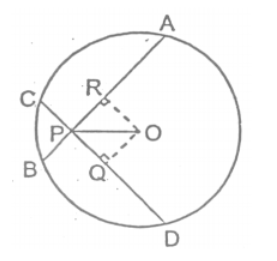
View SolutionIn Figure, O is the center of a circle and PO bisects ∠APD Prove that AB=CD
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View Solution