In the expansion of if the sum of odd terms is and the sum of even terms is tehn none of these
= P + Q (given) ...(i)
and
P - Q (given) ...(ii)
(i)
[ from Eqs (i) and (ii)]
(ii)
[ from Eqs . (i) and (ii)]
Topper's Solved these Questions
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - JEE Type Solved Example : (Matching Type Questions )
2 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise For Session 1
7 Videos
- AREA OF BOUNDED REGIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
23 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
16 Videos
Similar Questions
In the expansion of (x+a)n if the sum of odd terms is P and the sum of even terms is Q, then (a)P2−Q2=(x2−a2)n (b)4PQ=(x+a)2n−(x−a)2n (c)2(P2+Q2)=(x+a)2n+(x−a)2n (d)none of these
View SolutionIn the expansion of (x+a)n the sum of even
terms is E and that of odd terms is O, them O2+E2 is equal to
View SolutionIf o be the sum of odd terms and E that of even terms in the expansion of (x+a)n prove that: (i)O2−E2=(x2−a2)n (ii) 4OE=(x+a)2n−(x−a)2n (iii) 2(O2+E2)=(x+a)2n+(x−a)2n
View SolutionIf P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, prove that
(ii) 4PQ=(x+a)2n−(x−a)2nand
View SolutionIn the expansion of (x2+1+1x2)n,n∈N, number of terms is2n+1
View SolutionIn the expansion of (x2+1+1x2)n,n∈N, number of terms is2n+1
View SolutionIf the sum of odd terms and the sum of even terms in (x+a)n are p and q respectively then p2+q2=
View SolutionIf P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, prove that
(iii) 2(P2+Q2)=(x+a)2n+(x−a)2n.
View SolutionIf P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, prove that
(i) p2−Q2=(x2−a2)n
View Solution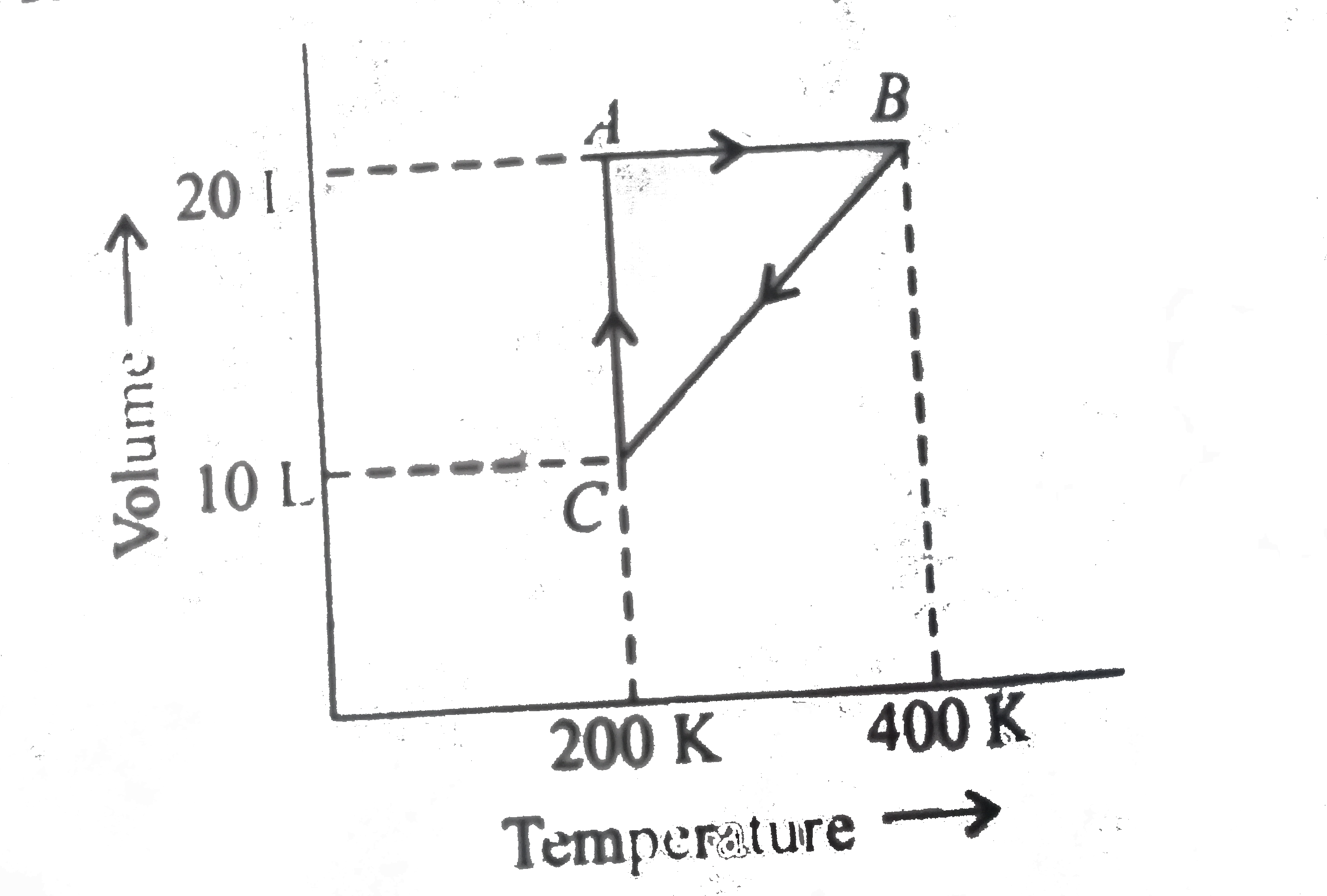
The pressures at A and B in the atmosphere are, respectively,
View Solution
