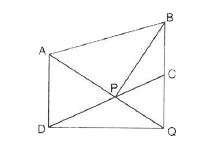
In the figure ABCD is a rectangle and P is a point on the side CD. Prove that the area of triangle A Q B is equal to the sum of the areas of triangle P Q D and Delta P C B.Solution in Malayalam
Step by step video & image solution for In the figure ABCD is a rectangle and P is a point on the side CD. Prove that the area of triangle A Q B is equal to the sum of the areas of triangle P Q D and Delta P C B. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that the.circumcentre of an equilateral triangle is the same as its centroid.
i) Calculate the length of a side. of an equilateral triangle with vertices on a circle of diameter 1 ceritimetre.
ii). Calculate the perimeter of such a triạngle.
View SolutionTriangles having equal areas and having one side of one of the triangles, equal to one side of the other, have their corresponding altitudes equal. GIVEN : Two triangles ABC and PQR such that: ar(ABC)=AR(PQR) (ii)AB=PQ
View SolutionABC is a triangle and PQ is a straight line meeting AB in P and AC in Q . If AP=1cm , PB=3cm , AQ=1.5cm , QC=4.5m , prove that area of APQ is one-sixteenth of the area of ABC .
View SolutionABCD is a parallelogram; any line through A cuts DC at a point P and BC produced at Q. prove that triangle BCP is equal in area to triangle DPQ.
View SolutionIn parallelogram ABCD, P is a point on side AB and Q is a point on side BC, prove that
(i) ΔCPDandΔAQD are equal in area.
(ii) area (ΔAQD)= area of ΔAPD+ area of ΔCPB
View Solutionएक समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर क्रमशः बिंदु P और Q है। दर्शाइए कि : ΔAPB क्षेत्रफल =ΔBQC का क्षेत्रफल ।
View SolutionIf p,q are two-collinear vectors such that (b−c)p×q+(c−a)p+(a−b)q=0 where a, b, c are lengths of sides of a triangle, then the triangle is
View SolutionIn a triangle ABC , let P and Q be points on AB and AC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionIn two similar triangles ABC and PQR , if their corresponding altitudes AD and PS are in the ratio 4:9, find the ratio of the areas of triangle ABC and triangle PQR .
View SolutionABC is a triangle and PQ is a straight line meeting AB in P and AC in Q . If AP=1cm , PB=3cm , AQ=1.5cm , QC=4.5cm , prove that area of ΔAPQ is one-sixteenth of the area of ΔABC .
View SolutionABC is a triangle right angled at B;and P is the mid-point of AC . Prove that: PQ ⊥AB (ii) Q is the mid point of AB PB=PA=12AC
View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.

View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionIf p,q are two-collinear vectors such that (b−c)p×q+(c−a)p+(a−b)q=0 where a, b, c are lengths of sides of a triangle, then the triangle is
View Solution
