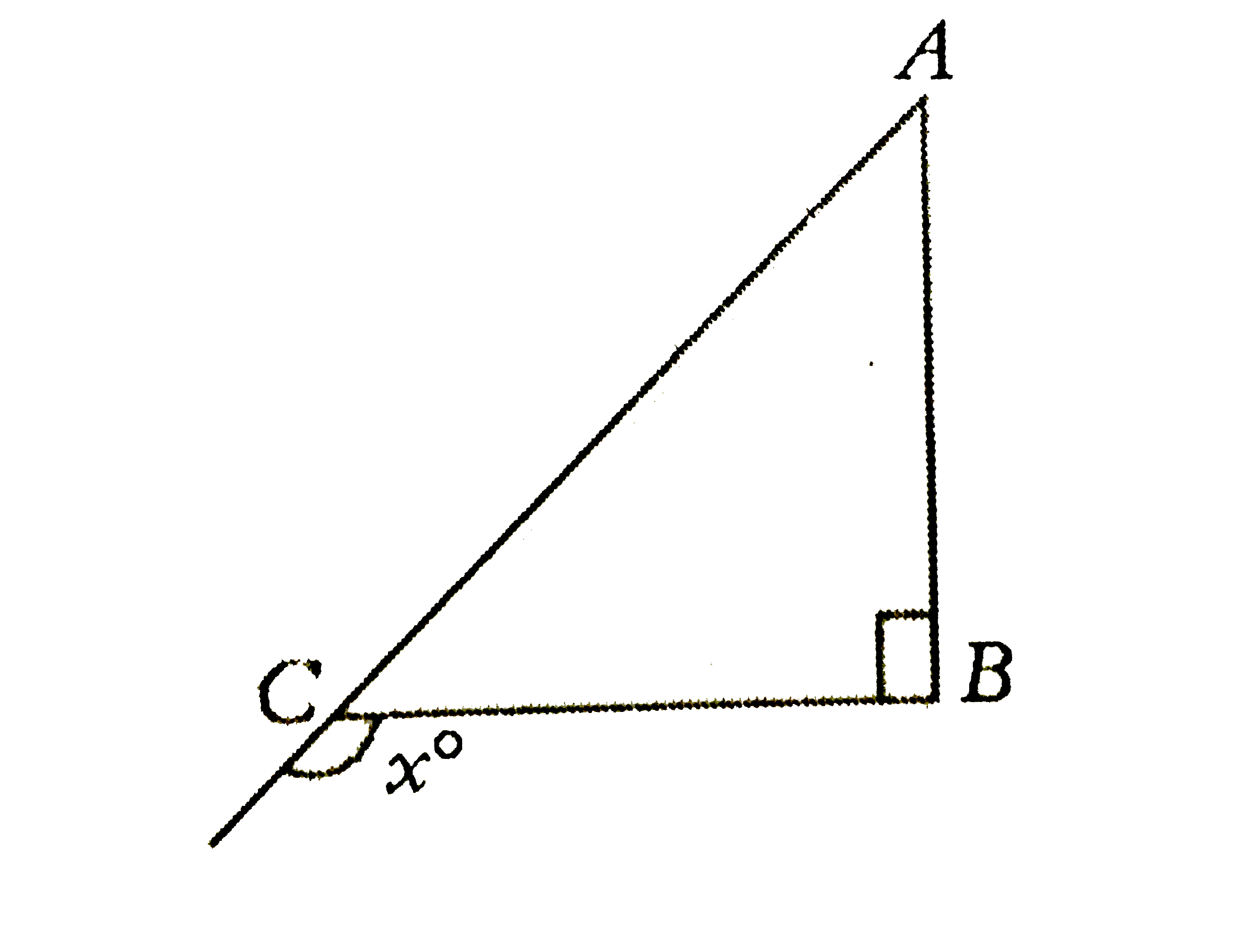
In the figure above, ABC is a right triangle and BC=AB , then find x∘.
45∘
90∘
120∘
135∘
The correct Answer is:D
Step by step video, text & image solution for In the figure above, ABC is a right triangle and BC=AB , then find x^(@). by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Similar Questions

In the figure above, ABC is a triangle in which BC=10 cm and AC=13 cm. If AD is the perpendicular bisector of BC, then find the length of AD.
View Solution
In the figure above, ABC is a triangle in which BC=24 cm and AC=13 cm. If AD is the perpendicular bisector of BC, then find the length of AD.
View Solution
Knowledge Check

In the figure above, ABC is a triangle in which BC=10 cm and AC=13 cm. If AD is the perpendicular bisector of BC, then find the length of AD.A12 cmB13 cmC10 cnD5 cm
In the figure above, ABC is a triangle in which BC=24 cm and AC=13 cm. If AD is the perpendicular bisector of BC, then find the length of AD.A7 cmB12 cmC13 cmD5 cm
In the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that

AB2=BC×BD
View SolutionIn the following figure, ABC is a right angled triangle at A. Find the area of the shaded region If AB = 6 cm, BC = 10 cm and I is the center of incircle of ΔABC
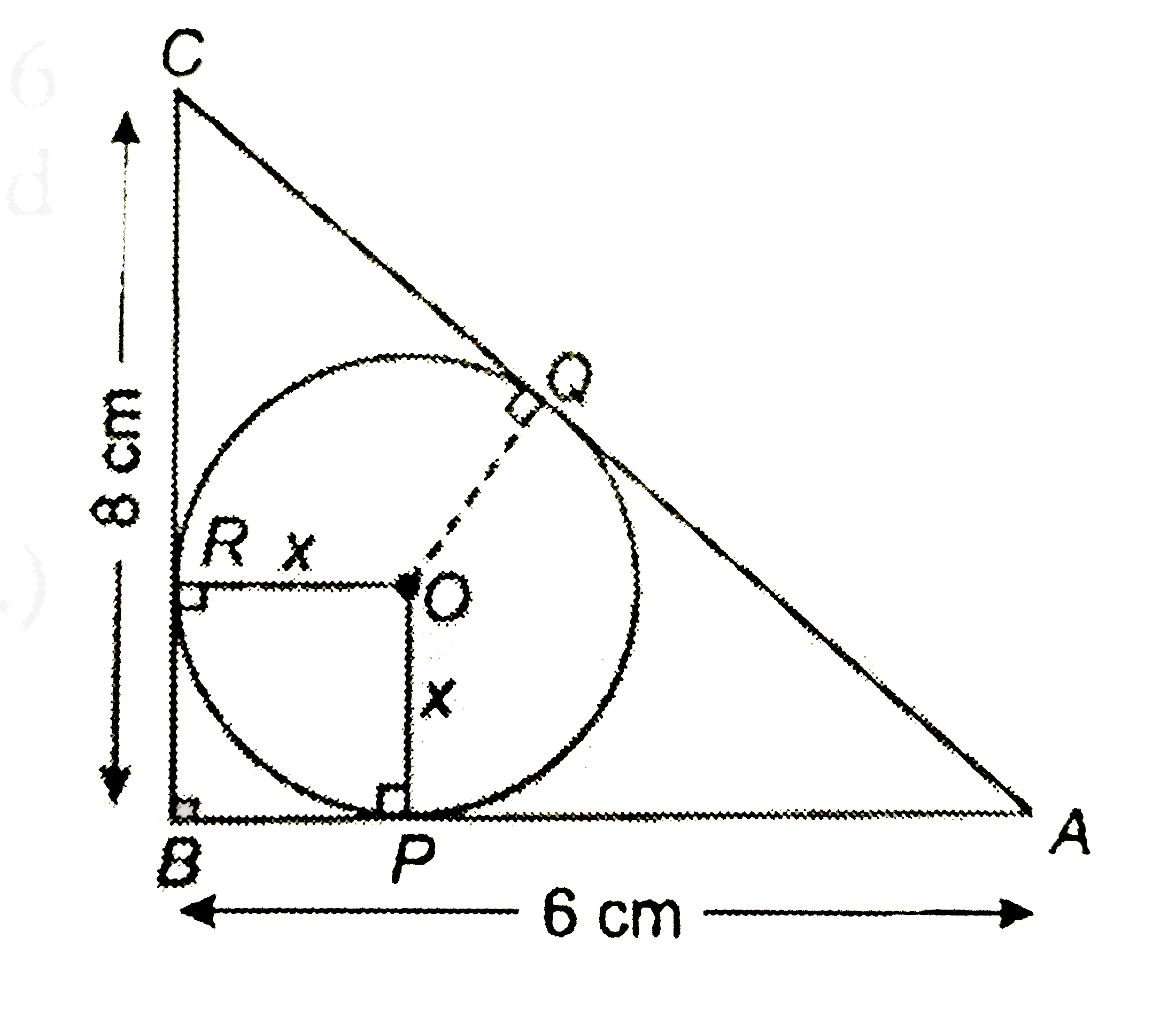
View SolutionIn the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
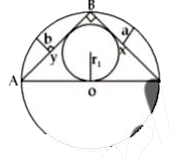
View SolutionIn the given figure, ABC is a right triangle inscribed in a circle of radius R. If r is the inradius, a is the sagitta of chord BC and b is the Sagitta of chord AB. Find R & r in terms of a & b.
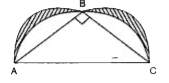
View SolutionIn the given figure, ABC is a right angled triangle with B as right angle. Three semicircles are drawn with AB, BC and AC as diameters. What is the area of the shaded portion, if the area of ΔABC is 12 square units ?
View SolutionIn the given figure, ABC is a right angled triangle, right -angled at A in which AB=6cm,BC=10cm and I is the incentre of ΔABC.
Find the area of the shaded region. [Take π=3.14]

View Solution
