In the figure AHKF, FKDE and HBCK are unit squares, AD and BF intersect in X. Then the ratio of the areas fo triangles AXF and ABF is-

A
1//4
B
1//5
C
1//6
D
1//8
Video Solution
Text Solution
The correct Answer is:B
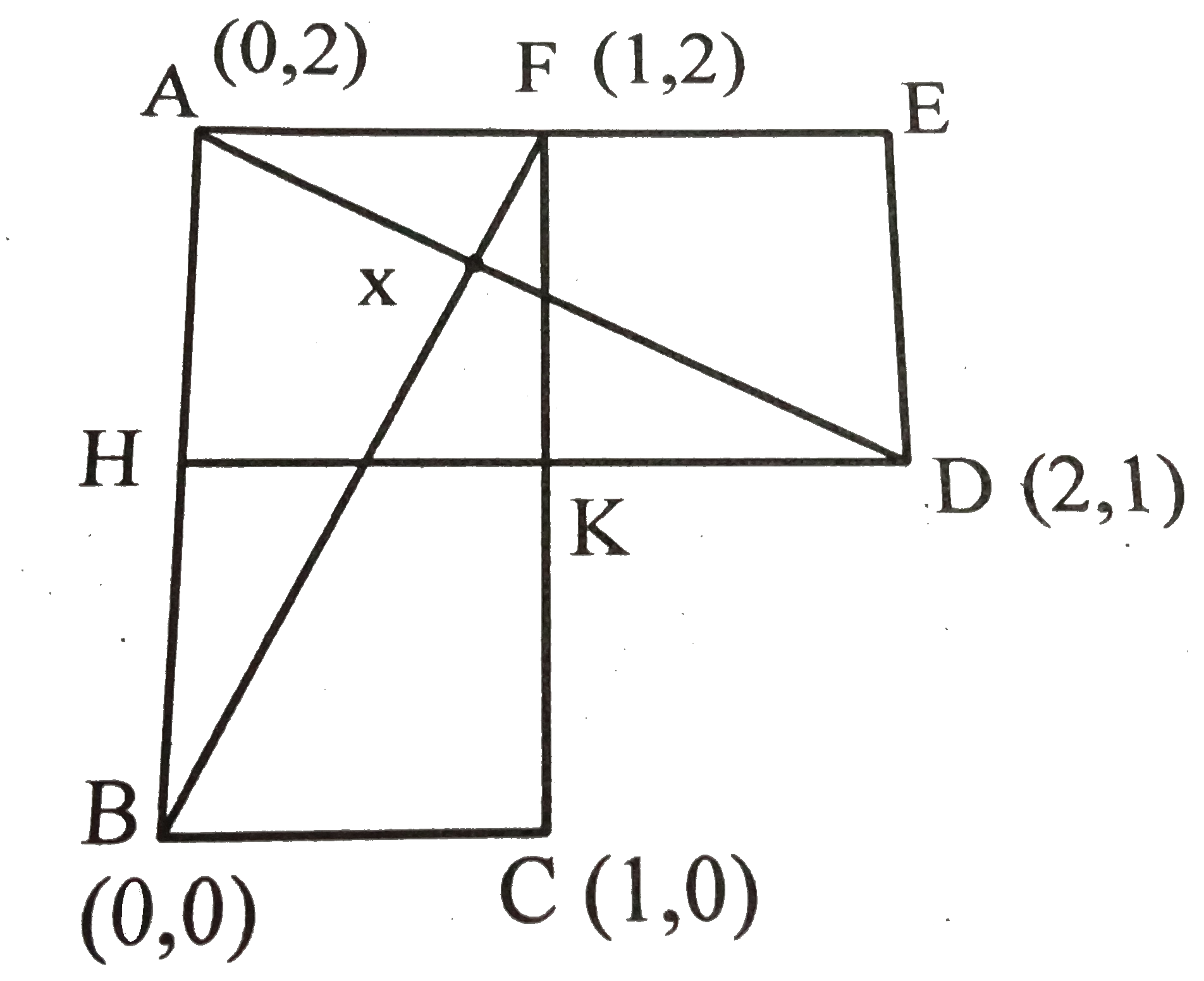
Equation of BF
y=2x
equation of AD x+2y=4
x(45,85)
ar(ΔAFX)ar(ΔABF)=12×1×(2−85)12×1×2=15
|
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHEMATICS
5 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2(MATHEMATICS)
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - exercise
18 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Knowledge Check
In the figure, ABCD is a square. E and Fare midpoints of AD and BC respectively. The ratio of areas of ΔGAB and ΔHAB
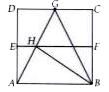 A4 : 1B1 : 4C1 : 2D2 : 1
A4 : 1B1 : 4C1 : 2D2 : 1In the right angle triangle ∠C=90∘. AE and BD are two medians of a triangle ABC meeting at F. The ratio of the area of △ABF and the quadrilateral FDCE is :
AA) 1:1BB) 1:2CC) 2:1DD) 2:3
In a ΔABC,∠B=90∘, median AD and CF intersects at 'O' . Find the ratio of area of ΔAOCandBDOF.
View SolutionIn a triangle ABC, median BE and CF intersect at O. Find the ratio of area of ΔOFEandΔABC.
View SolutionIn △ABC, the medians AD. BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View SolutionIn △ABC , the medians AD, BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View SolutionABCD is a parallelogram. E is a point on BC such that BE : EC = m:n. If AE and DB intersect in F, then what is the ratio of the area of triangle FEB to the area of triangle AFD?
View SolutionIn a ΔABC,∠B=90∘, median AD and CF intersects at 'O' . Find the ratio of area of ΔAOCandBDOF.
View Solution


