ABCD is a parallelogram. E is a point on BC such that BE : EC = m:n. If AE and DB intersect in F, then what is the ratio of the area of triangle FEB to the area of triangle AFD?
mn
(mn)2
(nm)2
[mm+n]2
To solve the problem, we need to find the ratio of the area of triangle FEB to the area of triangle AFD in the given parallelogram ABCD, where E is a point on BC such that BE : EC = m : n.
1. Draw the Parallelogram:
Begin by sketching the parallelogram ABCD. Label the vertices A, B, C, and D appropriately.
Hint: Remember that opposite sides of a parallelogram are equal and parallel.
2. Identify Point E:
Mark point E on side BC such that the ratio BE : EC = m : n. This means that if BE = m units, then EC = n units.
Hint: You can express the total length of BC as (m + n) units.
3. Draw Diagonals:
Draw diagonal BD. This will help in identifying the intersection point F where lines AE and BD intersect.
Hint: Diagonals of a parallelogram bisect each other, which can be useful in some problems.
4. Label the Intersection Point:
Let the intersection of lines AE and BD be point F.
Hint: Keep track of all points and their relationships to avoid confusion later.
5. Establish Similar Triangles:
Notice that triangles FEB and AFD share the angle at F. Since AE and BD are transversals intersecting parallel lines (AB and CD), triangles FEB and AFD are similar.
Hint: Use the properties of similar triangles to relate their areas.
6. Area Ratio of Similar Triangles:
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Thus, we can write:
Area of △FEBArea of △AFD=(BEAD)2
7. Expressing BE and AD:
From the ratio BE : EC = m : n, we can express BE as mm+n of the total length of BC. Since AD is equal to the total length of BC, we have:
AD=m+n
8. Substituting Values:
Substitute the values into the area ratio:
Area of △FEBArea of △AFD=(BEAD)2=(mm+n)2
9. Final Ratio:
Thus, the final ratio of the areas is:
Area of △FEBArea of △AFD=m2(m+n)2
Conclusion:
The ratio of the area of triangle FEB to the area of triangle AFD is m2(m+n)2.
Begin by sketching the parallelogram ABCD. Label the vertices A, B, C, and D appropriately.
Mark point E on side BC such that the ratio BE : EC = m : n. This means that if BE = m units, then EC = n units.
Draw diagonal BD. This will help in identifying the intersection point F where lines AE and BD intersect.
Let the intersection of lines AE and BD be point F.
Notice that triangles FEB and AFD share the angle at F. Since AE and BD are transversals intersecting parallel lines (AB and CD), triangles FEB and AFD are similar.
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Thus, we can write:
Area of △FEBArea of △AFD=(BEAD)2
From the ratio BE : EC = m : n, we can express BE as mm+n of the total length of BC. Since AD is equal to the total length of BC, we have:
AD=m+n
Substitute the values into the area ratio:
Area of △FEBArea of △AFD=(BEAD)2=(mm+n)2
Thus, the final ratio of the areas is:
Area of △FEBArea of △AFD=m2(m+n)2
The ratio of the area of triangle FEB to the area of triangle AFD is m2(m+n)2.
Similar Questions
In △ABC, D and E are the points on sides AB and BC respectively such that DE || AC. If AD : DB = 5 : 3, then what is the ratio of the area of △BDE to that of the trapezium ACED?
View SolutionIn the given figure, E and F are the centers of two identical circles. What is the ratio of area of triangle AOB to the area of triangle DOC ?
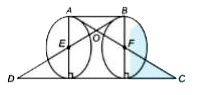
View Solution
Knowledge Check
If D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
A1:4B1:2C1:3D2:3ABC is a triangle with base AB. D is a point on AB such that AB = 5 and DB = 3. What is the ratio of the area of ΔADC to the area of ΔABC ?
A3/2B2/3C3/5D2/5ABC is a triangle with base AB. D is a point on AB such that AB = 5 and DB = 3. What is the ratio of the area of ΔADC to the area of ΔABC ?
A32B23C35D25
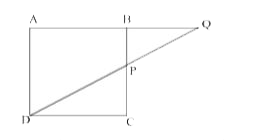
In the given figure, ABCD is a parallelogram. Point P is at BC such that PB : PC = 1 : 2. The extended DP and extended AB meets at point Q. If the area of BPQ is 20 unit2 then find the area of ΔDCP.
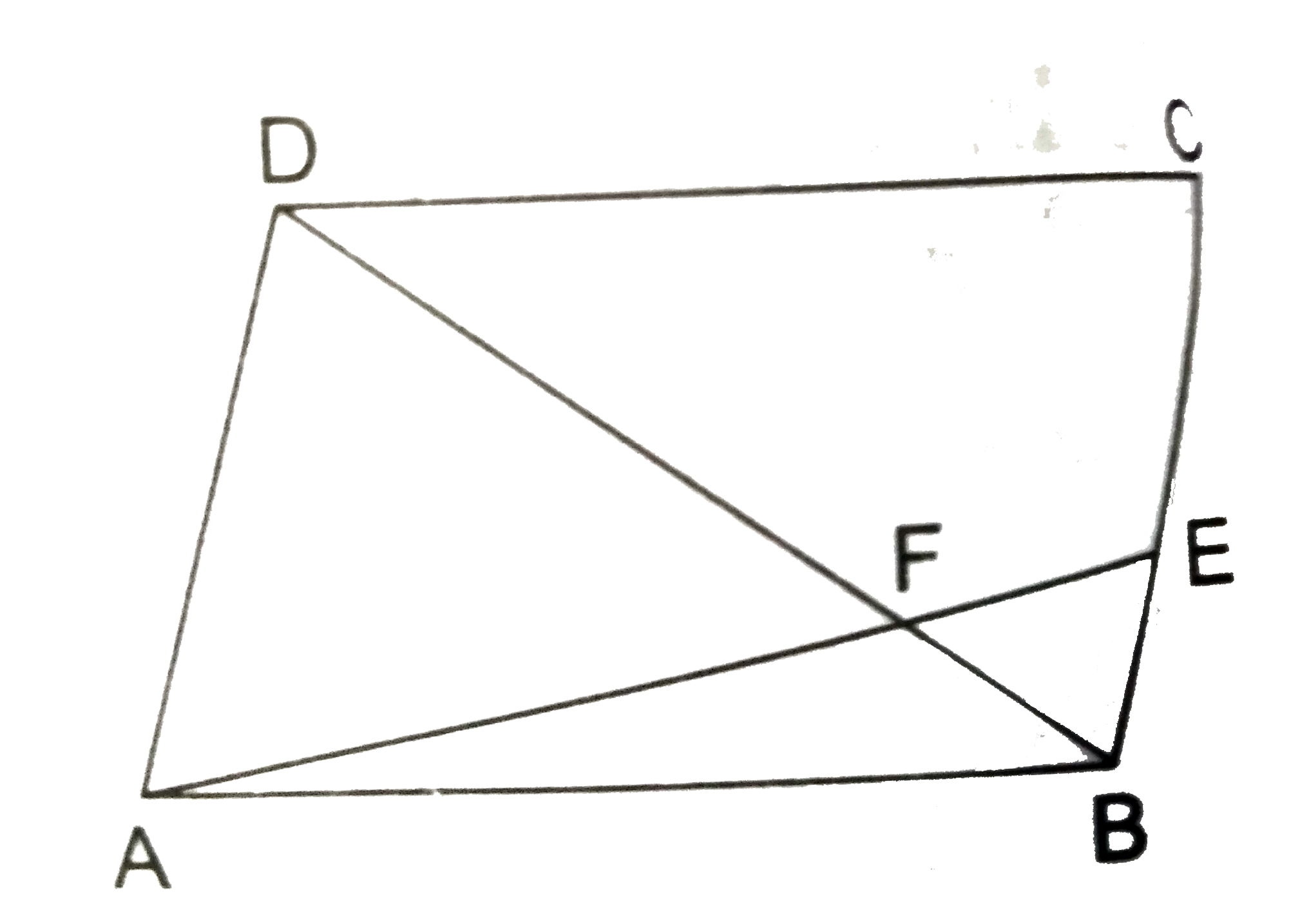
View SolutionABCD is a parallelogram and E is a point, on BC. If the diagonal BD intersects AE at F, prove that AF×FB×EF×FD.
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2EA and F is a point on Do such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third area of parallelogram AB CD
View SolutionIn ΔABC,D and E are the points on sides AB and BC respectively such that DE || AC. If AD : DB = 5 : 3, then what is the ratio of the area of ΔBDE to that of the trapezium ACED ?
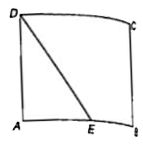
View SolutionABCD is a square , E is a point on AB such that BE=17 cm. The area of triangle ADE is 84 cm2 . What is the area of square ?
View Solution