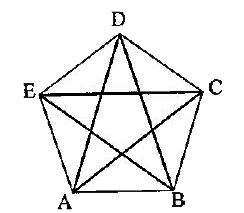
In the figure ¯¯¯¯¯¯AC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BD,¯¯¯¯¯¯BE and (CE) are diagonals. Is ¯¯¯¯¯¯BC a diagonal. Why or why not?
If you try to join adjacent vertices, will the result be a diagonal? Name all the sides, adjacent vertices of the figure ABCDE. Solution in Punjabi
Step by step video & image solution for In the figure bar(AC), bar(AD), bar(BD), bar(BE) and (CE) are diagonals. Is bar(BC) a diagonal. Why or why not? If you try to join adjacent vertices, will the result be a diagonal? Name all the sides, adjacent vertices of the figure ABCDE. by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BASIC GEOMETRICAL IDEAS BOOK - NAND LAL PUBLICATIONCHAPTER - BASIC GEOMETRICAL IDEAS EXERCISE - THINK DISCUSS AND WRITE
1 Videos
- BASIC GEOMETRICAL IDEAS BOOK - NAND LAL PUBLICATIONCHAPTER - BASIC GEOMETRICAL IDEAS EXERCISE - EXERCISE 4.1
20 Videos
- BASIC GEOMETRICAL IDEAS BOOK - NAND LAL PUBLICATIONCHAPTER - BASIC GEOMETRICAL IDEAS EXERCISE - TRY THESE
5 Videos
- ALGEBRABOOK - NAND LAL PUBLICATIONCHAPTER - ALGEBRAEXERCISE - SAMPLE PAPER FOR PRACTICE
26 Videos
- DECIMALSBOOK - NAND LAL PUBLICATIONCHAPTER - DECIMALSEXERCISE - TRY THESE
13 Videos
Similar Questions
Look at the fig. (4.18). What is the name of the angle? Shall we say ∠P? But then which one do you mean? By ∠P what do we mean?

View SolutionUse the figure to name
(a) Five points
(b) A line
(c) Four rays
(d) Five line segments.

View SolutionTry to find more examples for line segments from you surroundings.
View SolutionCoefficient of the variable in the expression 3−2x2 is
View SolutionCan you write the following as decimals?
View SolutionIn the figure 11.34, ABCD is a quadrilateral in which bar(AB) = bar(AD) and bar(BC) =bar(DC). Diagonals bar(AC) and BD intersect each other at O.Show that-
View SolutionIn the figure given below, bar(ED)||bar(AB) and bar(EF)||bar(BC) . If /_FED =40^(@) and /_ DEC =20^(@) , then the angle made by bar(BC) at the centre is
View SolutionIn the figure below, ¯¯¯¯¯¯AB∣∣∣∣¯¯¯¯¯¯FC,¯¯¯¯¯¯AE∣∣∣∣¯¯¯¯¯¯BC and ¯¯¯¯¯¯AF∣∣¯¯¯¯¯¯BD. If ∠F=x∘,∠C=γ∘,∠EAB=k∘ and ∠ABD=p∘, then which of the following options is correct ?
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_VIII_C16_E05_004_Q01.png" width="80%"gt
View Solution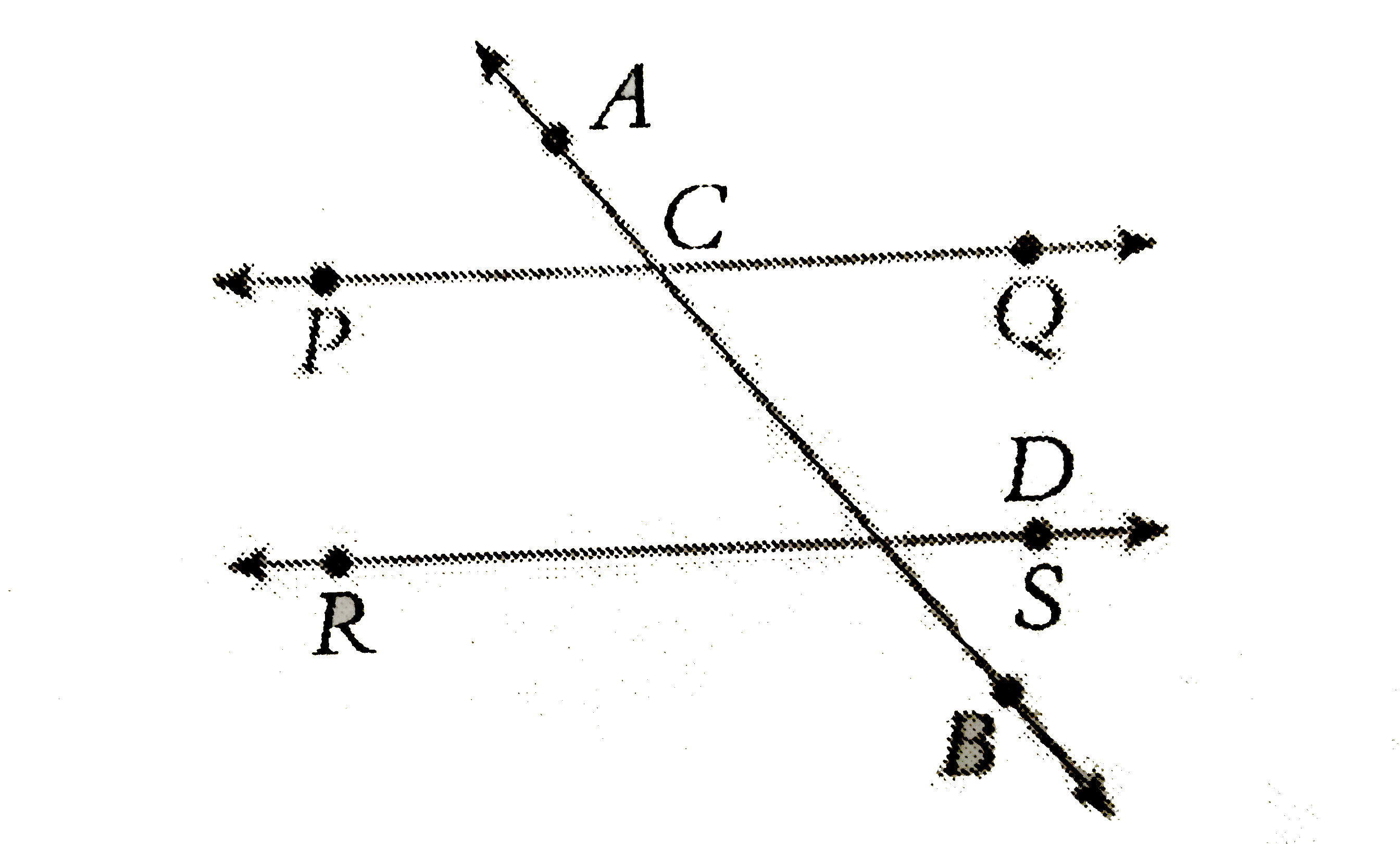
In the figure above, ¯¯¯¯¯¯PQand¯¯¯¯¯RS are parallel. ¯¯¯¯¯¯AC is transversal of ¯¯¯¯¯¯PQand¯¯¯¯¯RS. If ∠(ACP)=5x−70∘and∠BDR=4x+70∘, then find the value of x.
View SolutionIn the following figure, if O is the center of the circle and ¯¯¯¯¯¯AB is the diameter, then find ∠ACB.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E02_009_Q01.png" width="80%"gt
View SolutionIn the following figure, ¯¯¯¯¯¯BD is produced to E. If ¯¯¯¯¯¯AD is the angle bisector of ∠A, then find the ∠BCD.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E03_005_Q01.png" width="80%"gt
View SolutionIn the given figure, ¯¯¯¯¯¯AD and ¯¯¯¯¯¯BE intersect at C, such that BC = CE, ∠ABC=40∘ and ∠DEC=85∘. Find ∠BAC−∠CDE.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E04_027_Q01.png" width="80%"gt
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionIn the figure given below (not to scale), D is a point on the circle with center A and C is a point on the circle with centers B, ¯¯¯¯¯¯AD⊥¯¯¯¯¯¯BD and ¯¯¯¯¯¯BC⊥¯¯¯¯¯¯CA. Then which of the following is true?
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E06_004_Q01.png" width="80%"gt
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R01_E02_023_Q01.png" width="80%"gt
View Solution¯¯¯¯¯¯AC and ¯¯¯¯¯¯BD are the diagonals of the parallelogram ABCD. Prove that,
−−→AC+−−→BD=2−−→BC and −−→AC−−−→BD=2−−→AB
View Solution
