Show that the sum of the vectors represented by the sides ¯¯¯¯¯¯AB,¯¯¯¯¯¯DC of a quadrilateral ABCD as equivalent to the sum of the vectors represented by the diagonals ¯¯¯¯¯¯ACand¯¯¯¯¯¯DB.
To prove that the sum of the vectors represented by the sides ¯¯¯¯¯¯¯¯AB and ¯¯¯¯¯¯¯¯¯DC of a quadrilateral ABCD is equivalent to the sum of the vectors represented by the diagonals ¯¯¯¯¯¯¯¯AC and ¯¯¯¯¯¯¯¯¯DB, we can follow these steps:
1. Assign Vectors to Points:
Let the position vectors of points A,B,C, and D be represented as →A,→B,→C, and →D respectively.
2. Express Vectors:
We can express the vectors ¯¯¯¯¯¯¯¯AB, ¯¯¯¯¯¯¯¯¯DC, ¯¯¯¯¯¯¯¯AC, and ¯¯¯¯¯¯¯¯¯DB in terms of these position vectors:
- ¯¯¯¯¯¯¯¯AB=→B−→A
- ¯¯¯¯¯¯¯¯¯DC=→C−→D
- ¯¯¯¯¯¯¯¯AC=→C−→A
- ¯¯¯¯¯¯¯¯¯DB=→B−→D
3. Set Up the Equation:
We need to show that:
¯¯¯¯¯¯¯¯AB+¯¯¯¯¯¯¯¯¯DC=¯¯¯¯¯¯¯¯AC+¯¯¯¯¯¯¯¯¯DB
Substituting the expressions from step 2:
(→B−→A)+(→C−→D)=(→C−→A)+(→B−→D)
4. Simplify Both Sides:
The left-hand side simplifies to:
→B−→A+→C−→D=→B+→C−→A−→D
The right-hand side simplifies to:
→C−→A+→B−→D=→C+→B−→A−→D
5. Conclusion:
Since both sides are equal:
→B+→C−→A−→D=→C+→B−→A−→D
This confirms that:
¯¯¯¯¯¯¯¯AB+¯¯¯¯¯¯¯¯¯DC=¯¯¯¯¯¯¯¯AC+¯¯¯¯¯¯¯¯¯DB
Hence, we have proved that the sum of the vectors represented by the sides ¯¯¯¯¯¯¯¯AB and ¯¯¯¯¯¯¯¯¯DC is equivalent to the sum of the vectors represented by the diagonals ¯¯¯¯¯¯¯¯AC and ¯¯¯¯¯¯¯¯¯DB.
Let the position vectors of points A,B,C, and D be represented as →A,→B,→C, and →D respectively.
We can express the vectors ¯¯¯¯¯¯¯¯AB, ¯¯¯¯¯¯¯¯¯DC, ¯¯¯¯¯¯¯¯AC, and ¯¯¯¯¯¯¯¯¯DB in terms of these position vectors:
- ¯¯¯¯¯¯¯¯AB=→B−→A
- ¯¯¯¯¯¯¯¯¯DC=→C−→D
- ¯¯¯¯¯¯¯¯AC=→C−→A
- ¯¯¯¯¯¯¯¯¯DB=→B−→D
We need to show that:
¯¯¯¯¯¯¯¯AB+¯¯¯¯¯¯¯¯¯DC=¯¯¯¯¯¯¯¯AC+¯¯¯¯¯¯¯¯¯DB
Substituting the expressions from step 2:
(→B−→A)+(→C−→D)=(→C−→A)+(→B−→D)
The left-hand side simplifies to:
→B−→A+→C−→D=→B+→C−→A−→D
The right-hand side simplifies to:
→C−→A+→B−→D=→C+→B−→A−→D
Since both sides are equal:
→B+→C−→A−→D=→C+→B−→A−→D
This confirms that:
¯¯¯¯¯¯¯¯AB+¯¯¯¯¯¯¯¯¯DC=¯¯¯¯¯¯¯¯AC+¯¯¯¯¯¯¯¯¯DB
Hence, we have proved that the sum of the vectors represented by the sides ¯¯¯¯¯¯¯¯AB and ¯¯¯¯¯¯¯¯¯DC is equivalent to the sum of the vectors represented by the diagonals ¯¯¯¯¯¯¯¯AC and ¯¯¯¯¯¯¯¯¯DB.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC have the same magnitude R. Then the sum of these vectors have magnitude.
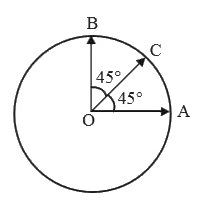 ARB√2RC3RD(1+√2)R
ARB√2RC3RD(1+√2)R - Question 2 - Select One
If D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
A2(¯¯¯¯¯¯AD−¯¯¯¯¯¯BD)B2(¯¯¯¯¯¯DC−¯¯¯¯¯¯BD)C2(¯¯¯¯¯¯BD−¯¯¯¯¯¯CA)D2(¯¯¯¯¯¯BD−¯¯¯¯¯¯AC) - Question 3 - Select One
If ABCD is quadrilateral whose sides represent vectors in cyclic order, →AB is equivalent is
A−−→CA+−−→CBB−−→CDC−−→AD+−−→DC+−−→CBD−−→AD+−−→BD
The vector area of a parallelogram with ¯a and ¯b as adjacent sides is
View SolutionWhat is the angle between ?
(i) ¯¯¯¯¯¯ABand¯¯¯¯¯¯AC
(ii) ¯¯¯¯¯¯ABand¯¯¯¯¯¯BC
 View Solution
View SolutionIf the vector −¯i+¯j−¯k bisects the angles between the vector ¯c and the vector 3¯i+4¯j ,then the unit vector in the direction of ¯c is
View SolutionLet O be the origin and A,B be two points, ¯p,¯q are vectors represented by ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and magnitudes are p,q respectively. Unit vector bisecting ∠AOB is
View SolutionIf the parallelogram ABCD with ¯¯¯¯¯¯AC as the diagonal is completed, then the position vector of the point D is
View Solution

