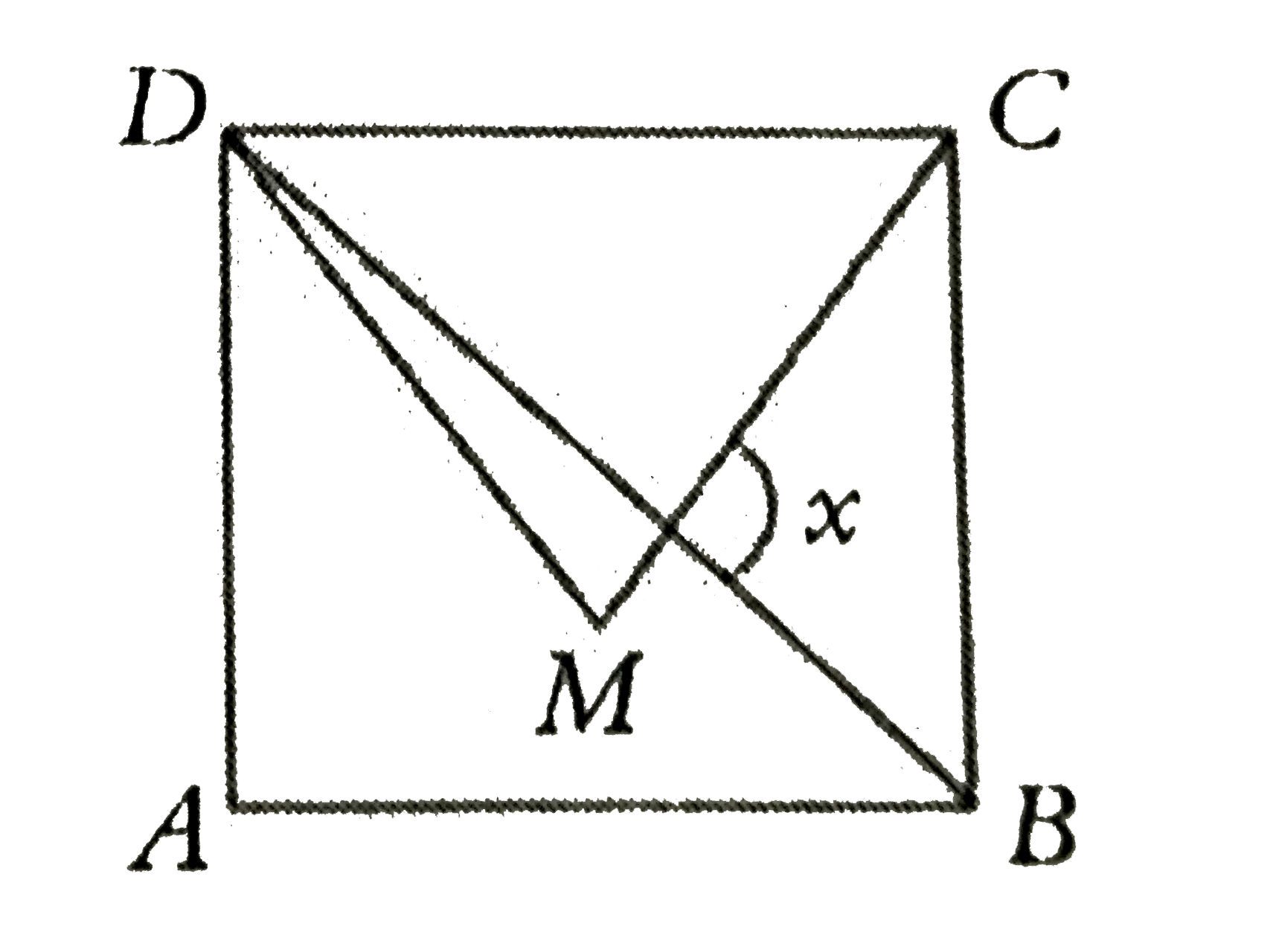
In the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
A
75∘
B
90∘
C
105∘
D
60∘
Video Solution
Text Solution
The correct Answer is:c
(i) The diagonal BD bisects ∠B and ∠D .
(ii) BCD is an isosceles righ angles triangle using this find ∠CBD.
(iiI) Given DMC is equilateral, so use this find ∠MCB.
(iv) Sum of the angles of a triangle is 180∘. Using this find ∠x.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 37videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - TEST YOUR CONCEPTS ( VERY SHORT ANSWER TYPE QUESTIONS)28videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 132videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 37videos
Formulae
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)7videos
INDICES
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a square and AOB is an equilateral triangle. What is the value of ∠DOC?
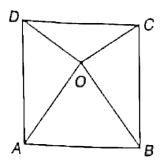 A120∘B150∘C125∘Dcan't be determined
A120∘B150∘C125∘Dcan't be determined - Question 2 - Select One
ABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of these - Question 3 - Select One
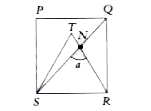
In the given figure, PQRS is a square and SRT is an equliateral triangle. What is the value (in digrees) of ∠SOR ?
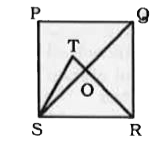 A45B55C60D75
A45B55C60D75
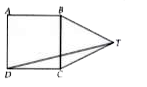
In the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP
 View Solution
View SolutionIn Figure, ABC is an equilateral triangle. Find m ∠BEC
View SolutionIn the given figure, ABCD is a square of side 6 cm and CDE is an equilateral triangle. Find the perimeter of the figure.
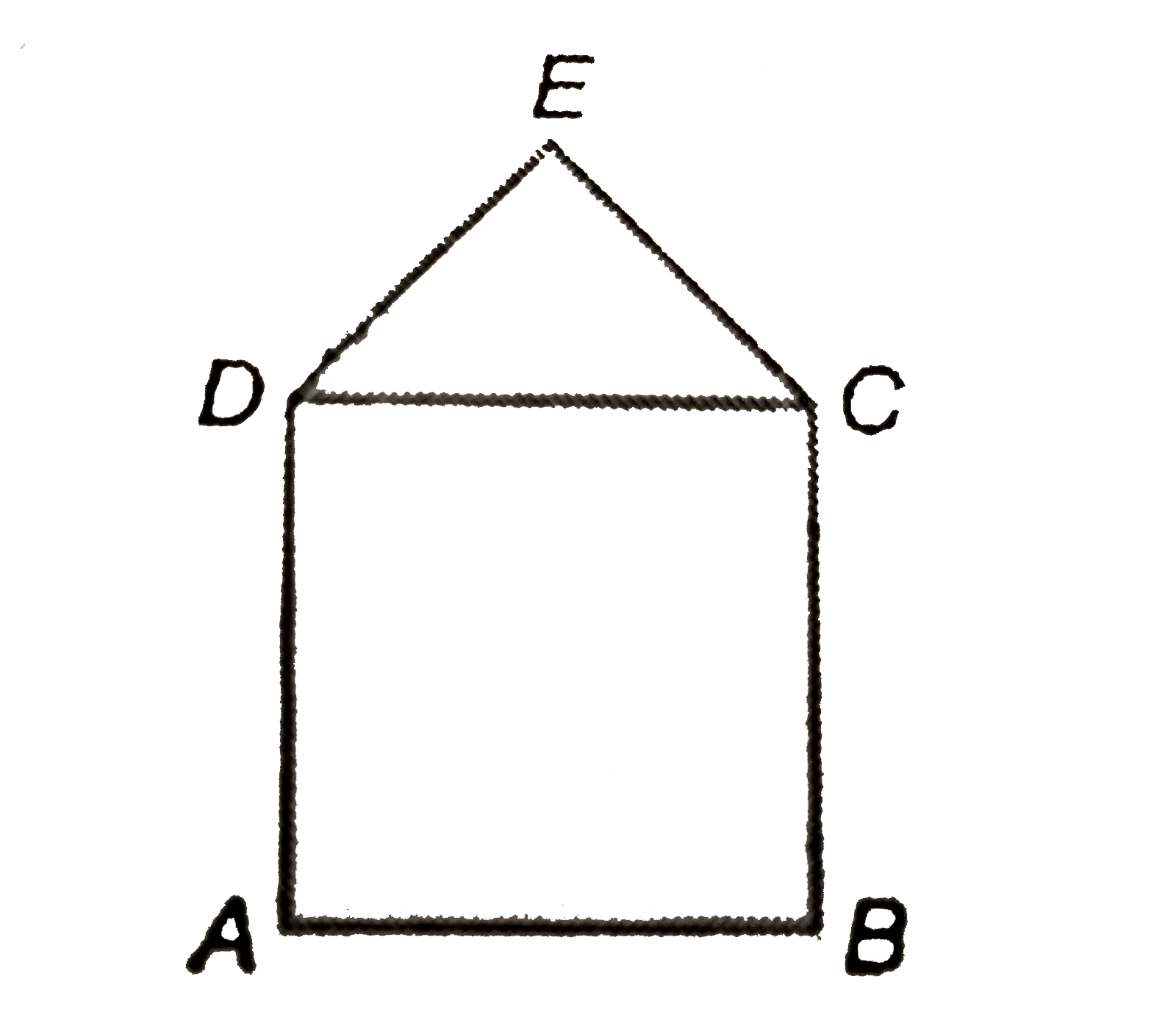 View Solution
View SolutionABCD is a square. Find x
View SolutionABCD is a square. Find x
View Solution