In the figure, chord AB ≅ chord CD
Prove that ,
ar AC ≅ arc BD
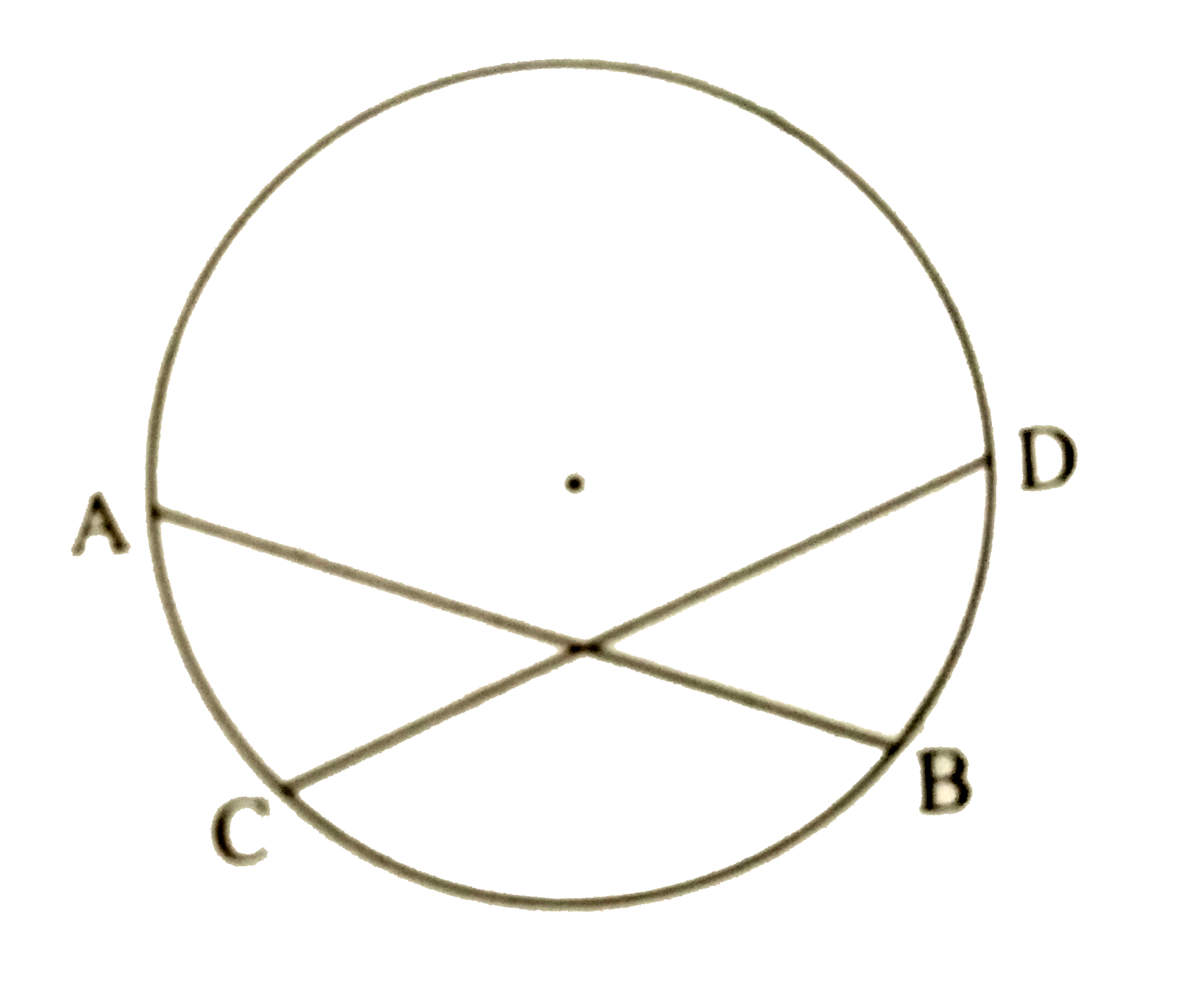
Chord AB≅ chord CD ….(Given )
∴ Arc ACB ≅ arc CBD …(Arcs corresponding to congruent chords )
∴ m (arc ACB ) = m (arc CBD ) ….(1)
But m ( arc ACB ) = m ( arc AC ) + m ( arc CB ) …..(2)
and m (arc CBD ) = m ( arc CB ) + m (arc BD ) ....(Arc addition postulate ) ....(3)
From (1 , (2) and (3) , we get
m (arc AC + m (arc CB ) = m (arc CB ) + m (arc BD )
∴ m (arc AC ) = m ( arc BD )
∴ arc ≅ arc BD.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.4 (1 mark each)9videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.5 (1 mark each)7videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.2 (1 mark each)9videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
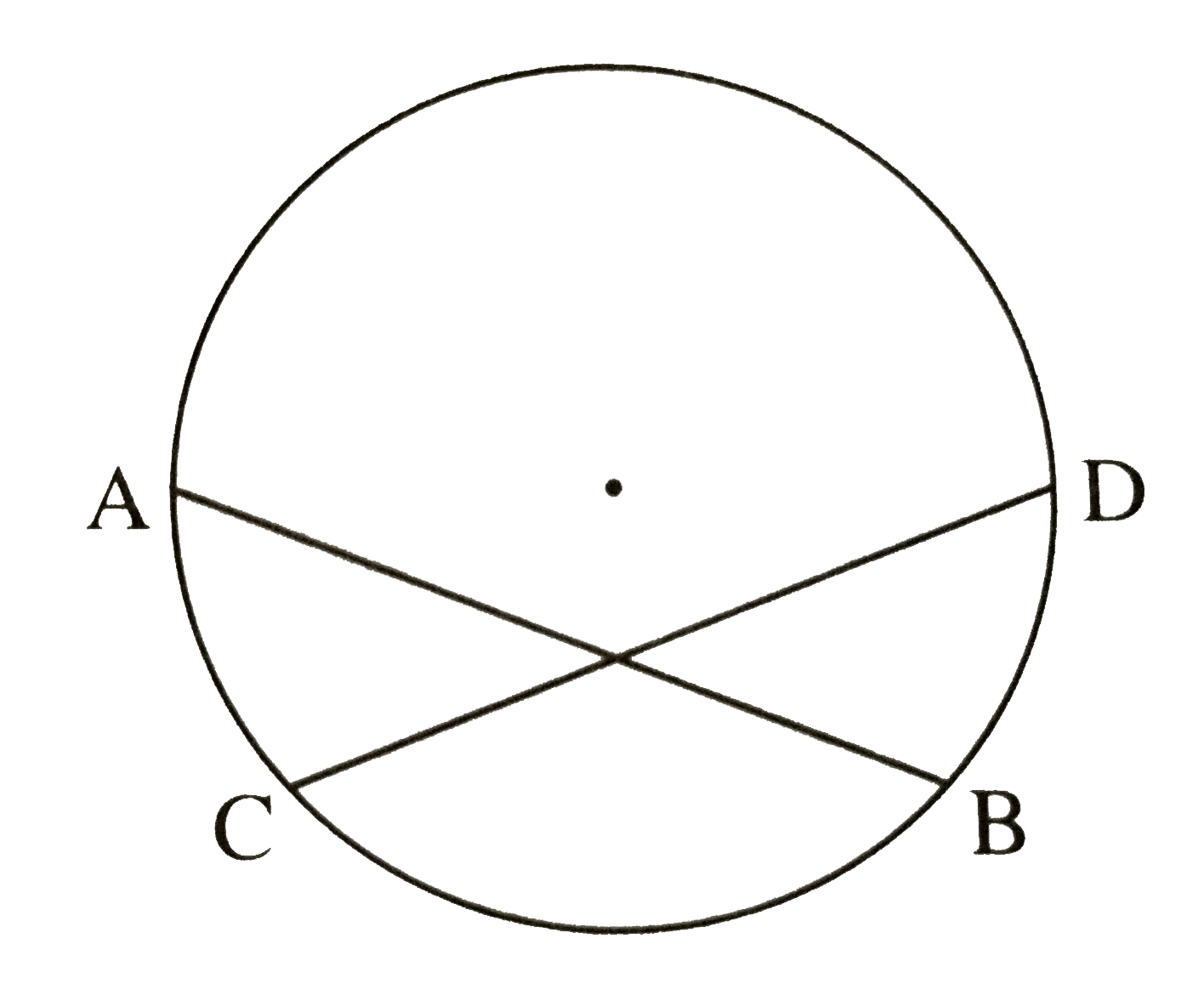
In figure, chord AB ≅ chord CD, Prove that, arc AC ≅ arc BD.
 View Solution
View SolutionIn the given figure, if AC = BD, then prove that AB = CD.
 View Solution
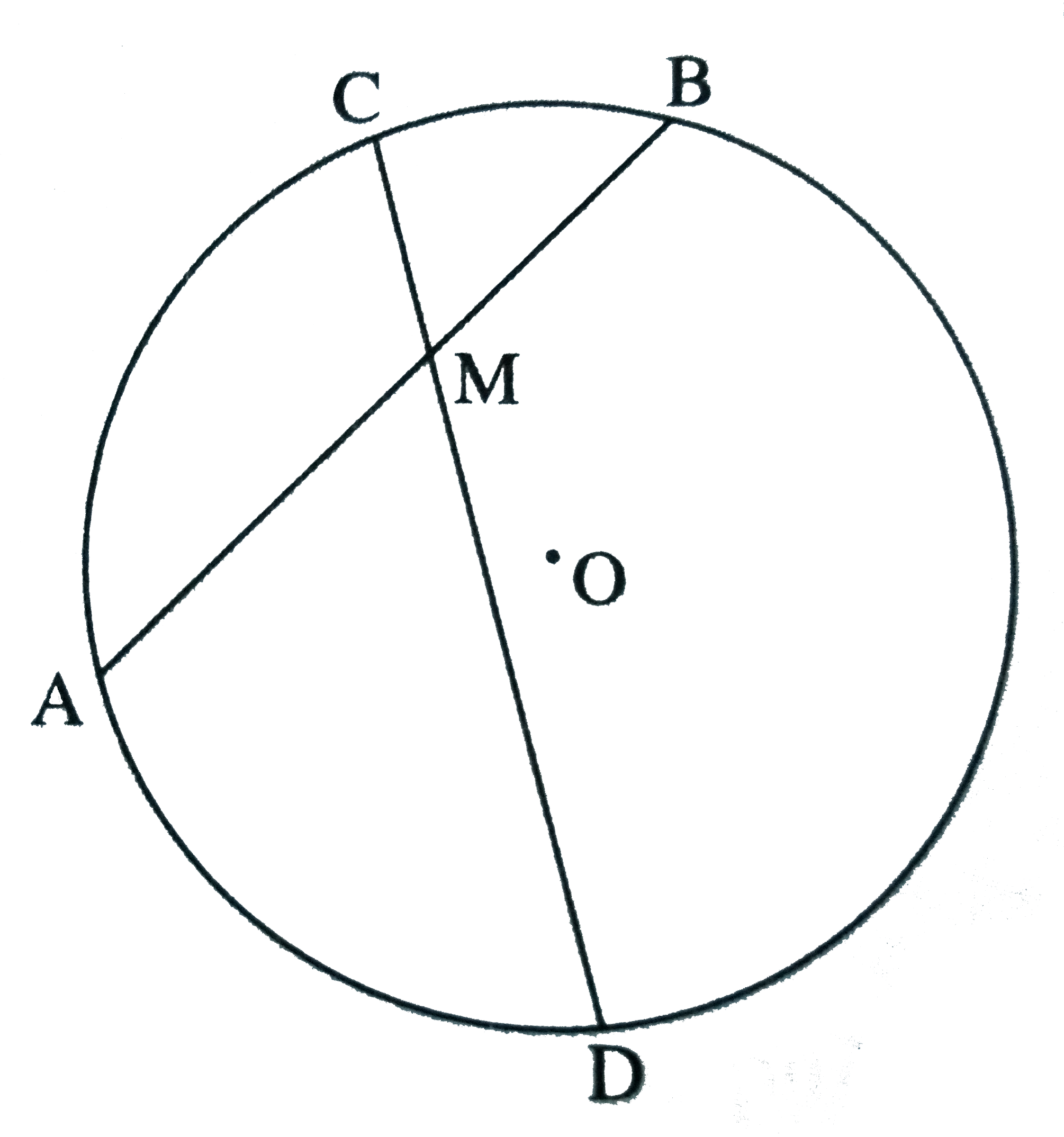
View SolutionIn the figure, chord AB and chord CD intersect at point M inside the circle such that AM=4, BM=3, CM=2, then CD=………
 View Solution
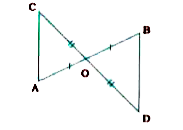
View SolutionIn the given figure AB and CD bisect each other at O. Prove that AC = BD.
 View Solution
View SolutionIn the figure, diameter AB and chord CD intersect in point E.
If m (arc CXB ) = 100∘. Find
(i) ∠ADC
(ii)∠CDB
(iii) ∠ACB
 View Solution
View SolutionIn the given figure below, if AC = BD then prove that AB = CD.
 View Solution
View SolutionIn the following figure, if AB = CD, prove that AC = BD. State the axioms used in proving the result.
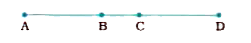 View Solution
View SolutionIn the figure, chords AC and DE intersect at B. If ∠ABE=108∘, m (arc AE ) =95∘, find m (arc DC).
 View Solution
View SolutionIn Figure O is the mid-point of AB and CD. Prove that AOC≅ BOD (b) AC=BD (iii) AC∣∣BD
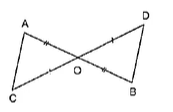 View Solution
View SolutionIn the given figure, two chords AC and BD of a circle intersect at E.If arcAB=arcCD, prove that : BE=EC and AE=ED
View Solution

