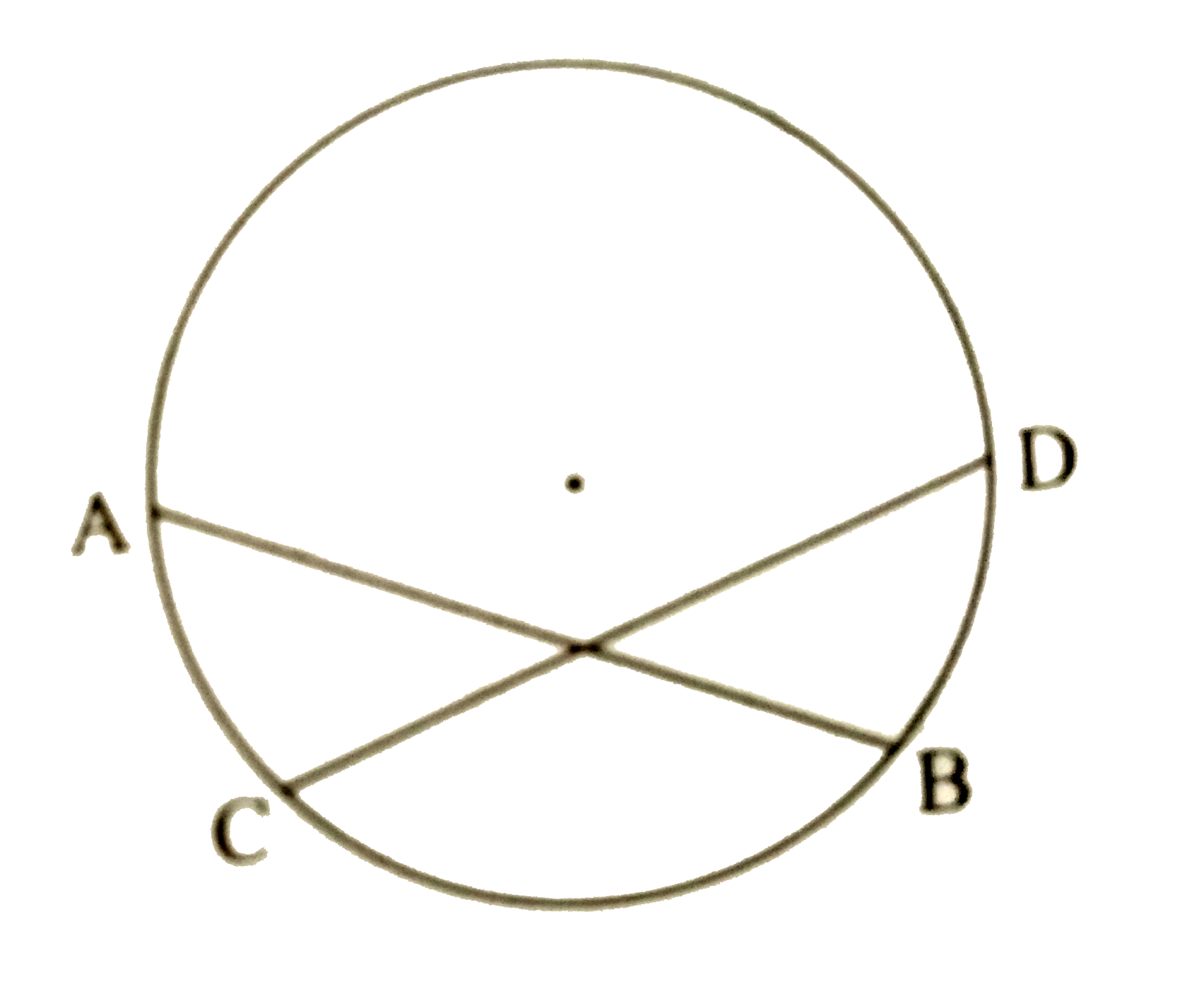
In figure, chord AB ≅ chord CD, Prove that, arc AC ≅ arc BD.
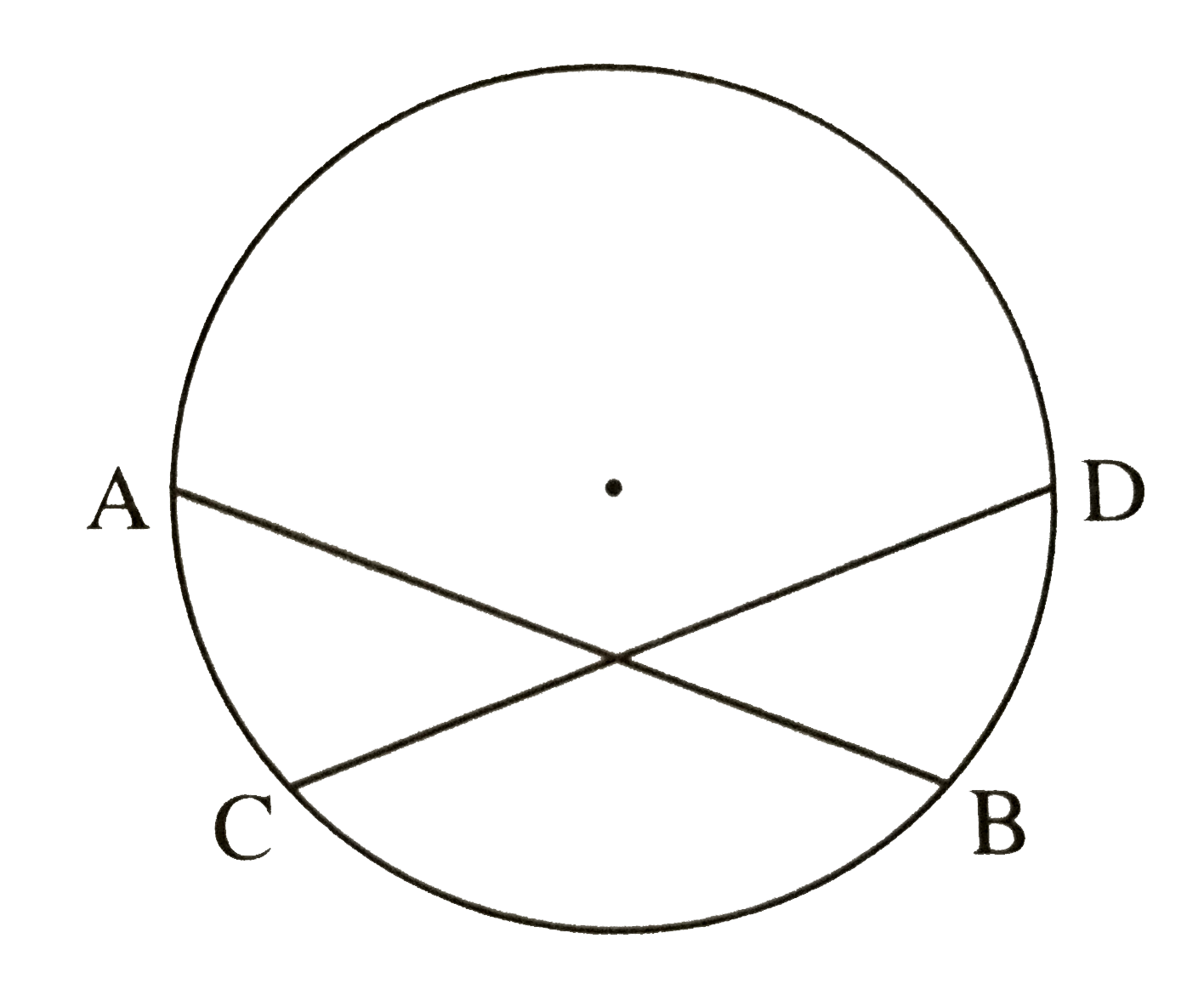
Chord AB ≅ chord CD ………( Given )
∴ArcACB≅arcCBD
………( Arcs corresponding to congruent chords )
∴m(arcACB)=m(arcCBD) ……(1)
But m(arcACB)=m(arcAC)+m(arcCB)……(2)
and m(arcCBD)=m(arcCB)+m(arcBD)……(3)
From (1),(2), and (3), we get,
m(arcAC)+m(arcCB)=m(arcCB)+m(arcBD)
∴m(arcAC)=m(arcBD)
∴arcAC≅arcBD.
Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.4
15 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.5
6 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.2
8 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
Knowledge Check
If AB≅CD then
AAB<CDBAB+CD=0CAB=CDDAB>CD
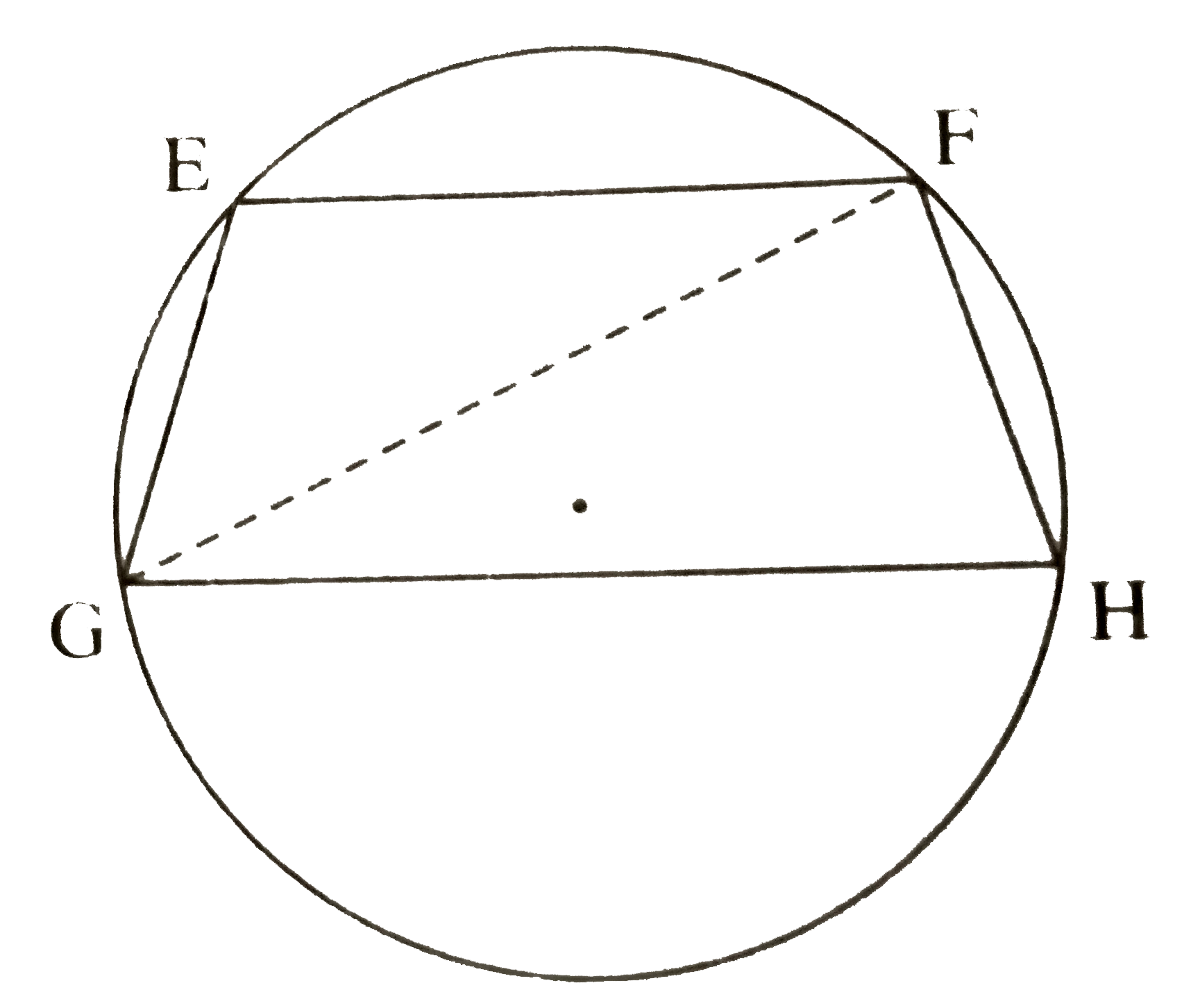
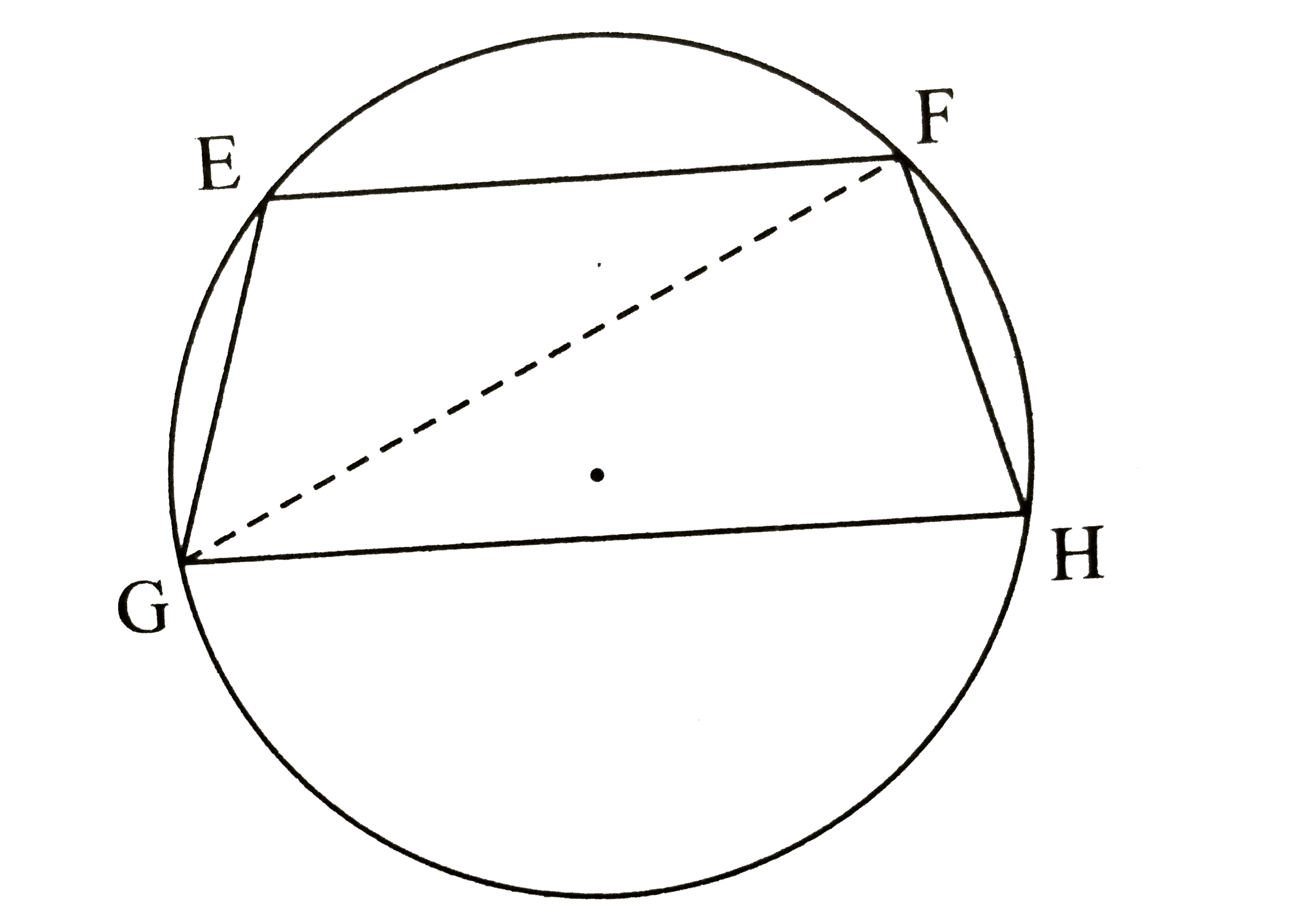
In the adjoining figure ,chord EF ∣∣ chord GH. Prove that, chord EG≅chord FH. Fill in the blanks and write the proof.
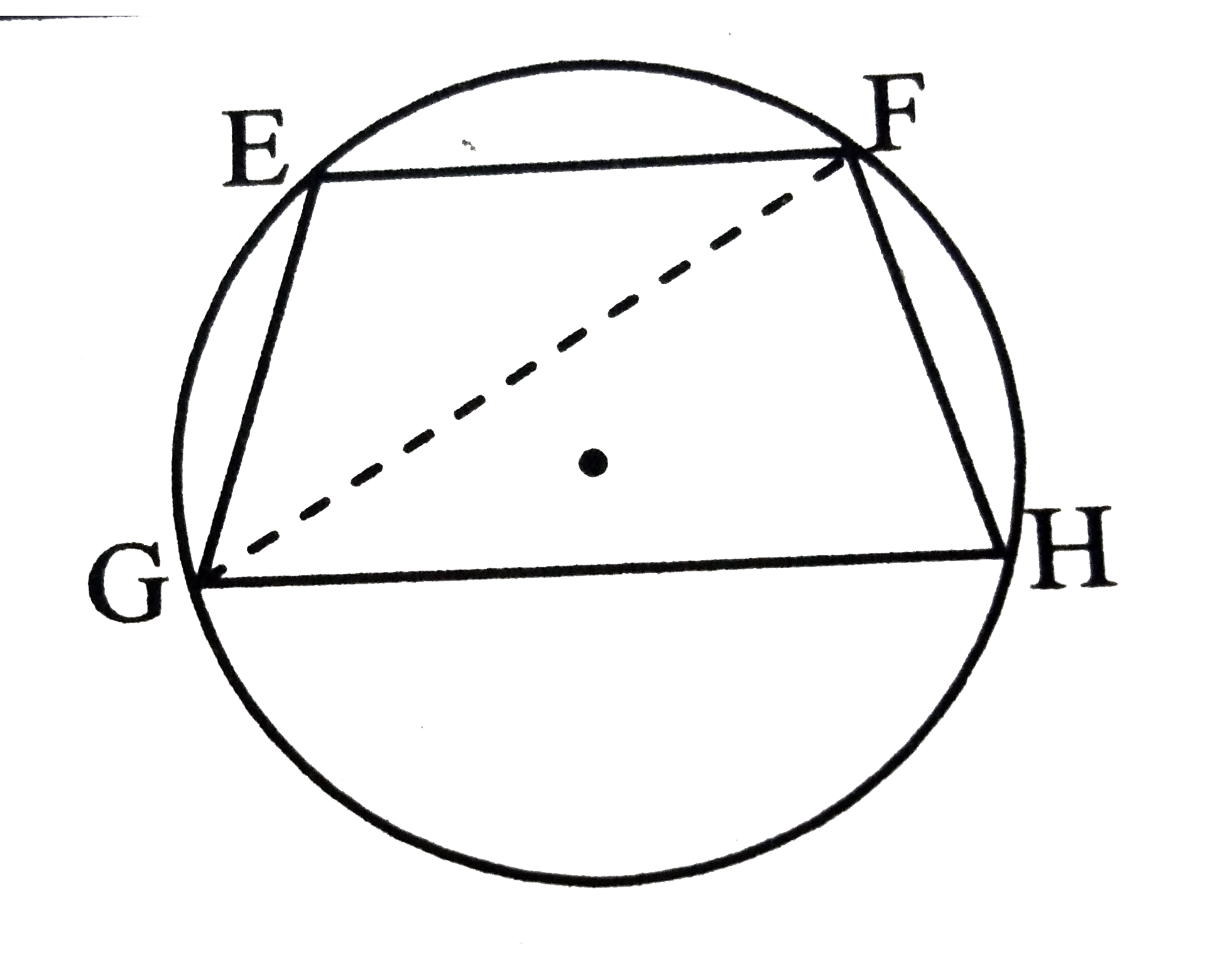
View SolutionIn the figure, chord EF∣∣ chord GH.
Prove that ,
chord EG ≅ chord FH .
Fill in the blanks and write the proof .
Proof : Draw seg GF.
∠EFG=∠FGH ….( □) …..(1)
∠EFG=□ …(Inscribed angle theorem ) ...(2)
∠FGH=□ ....(Inscribed angle theorem ) ...(3) ∴ m ( arc EG ) =□ ....[From (1), (2) and (3) ]
∴ Chord EG ≅ Chord FGH ....(Corresponding chords of congruent arcs )
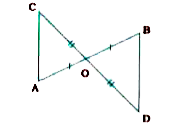
View SolutionIn the given figure AB and CD bisect each other at O. Prove that AC = BD.
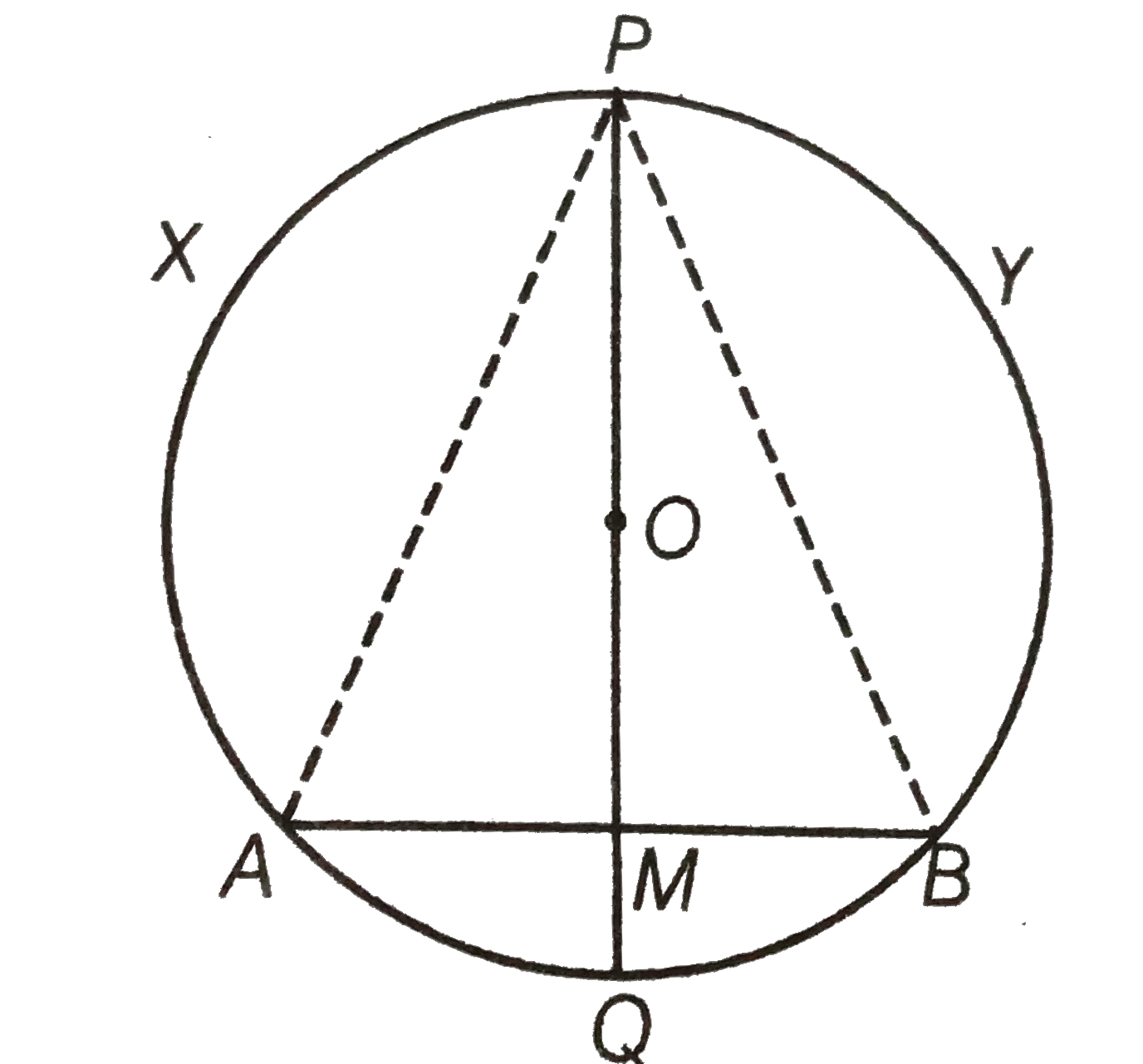
View SolutionIf the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA≅arc PYB.
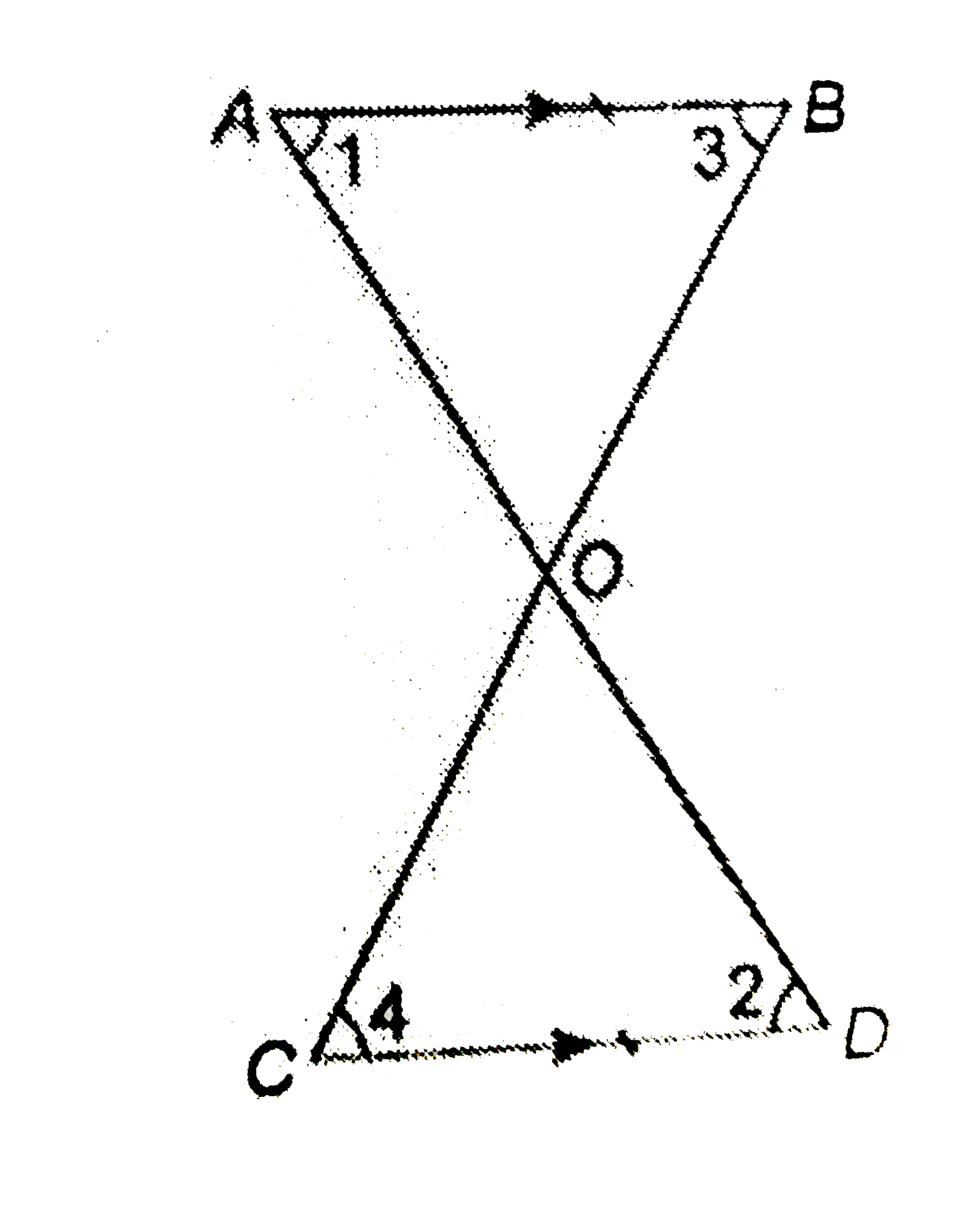
View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) ΔAOB≅ΔDOC
(ii) AD and BC bisect each other at the point O.
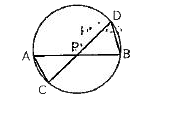
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB
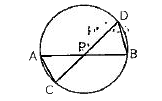
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : AP. PB = CP. DP
View Solution