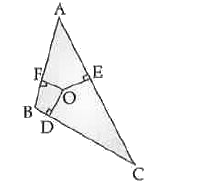
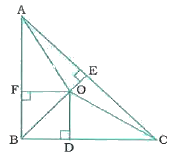
In the figure given below, O is point in the interior of a triangle ABC, OD⊥BC, OE⊥AC and OF⊥AB. Show that
(i) OA2+OB2+OC2+OD2−OE2−OF2=AR2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
 Solution in Kannada
Solution in Kannada
The correct Answer is:AE2+CD2+BF2
Step by step video, text & image solution for In the figure given below, O is point in the interior of a triangle ABC, OD _|_ BC, OE _|_ AC and OF _|_ AB. Show that (i) OA^(2) + OB^(2) + OC^(2) + OD^(2) - OE^(2) - OF^(2) = AR^(2) + BD^(2) + CE^(2) (ii) AF^(2) + BD^(2) + CE^(2) = AE^(2) + CD^(2) + BF^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - OSWAAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TEXTBOOK CORNER (EXERCISE 2.6)10videos
TRIANGLES
- BOOK - OSWAAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TEXTBOOK CORNER (EXERCISE 2.4)8videos
TRIANGLES
- BOOK - OSWAAL PUBLICATIONCHAPTER - SURFACE AREA AND VOLUMESEXERCISE - EXERCISE 15.55videos
SURFACE AREA AND VOLUMES
Similar Questions
In the figure given below, PS is the bisector of ∠QPR of ΔPQR . Prove that QSSR=PQPR
 06:33View Solution
06:33View SolutionLet ΔABC~ΔDEF and their areas be , respectively , 64cm2and121cm2 . If EF = 15.4 cm, find BC
06:26View SolutionA copper wire, 3mm in diameter , is wound about a cylinder whose length is 12cm, and diameter 10cm, so as to cover the curved surface of the cylinder . Find the length and mass of the wire, assuming the density of copper to be 8.88gpercm3
10:40View SolutionFrom a point O in the interior of a ABC , perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: (i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2 (ii) AF2+BD2+CE2=AE2+CD2+BF2
09:28View Solutionआकृति 6 . 54 में ΔABC के अभ्यन्तर में स्थित कोई बिंदु O है तथा OD⊥BC,OE⊥AC और OF⊥AB है दर्शाइए कि
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
 02:54View Solution
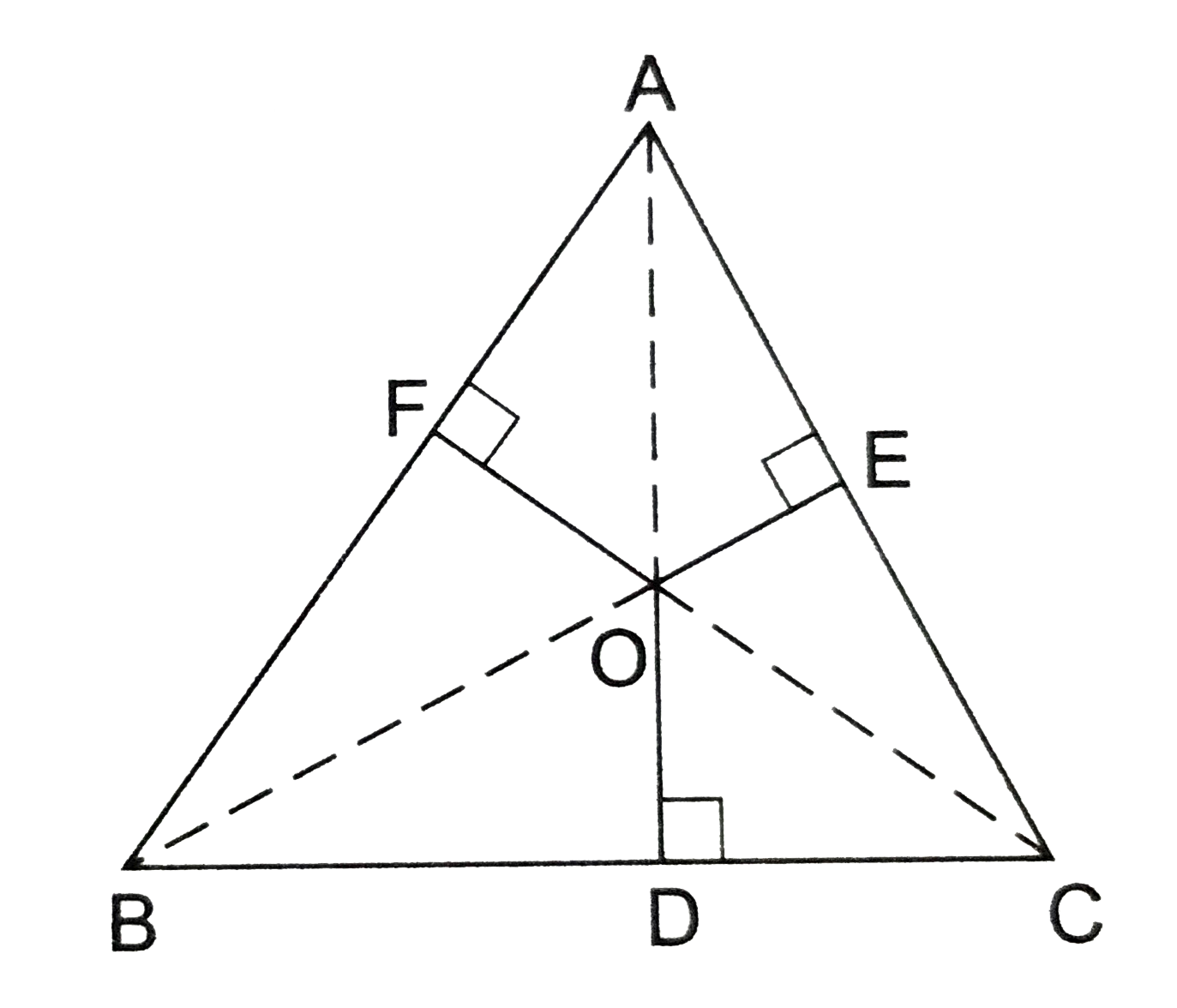
02:54View SolutionO is a point in the interior of ΔABC,OD⊥BC,OE⊥ACandOF⊥AB, as shown in the figure,
Prove that :
(i)OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AD2+BF2+CD204:37View Solution△ABC के एक अन्तः बिंदु O से, भुजा BC,CA तथा AB पर लम्ब क्रमशः OD,OE व OF खींचे गये है | सिद्ध कीजिए कि
(i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2
(ii) AF2+BD2+CE2=AE2+CD2+BF2View SolutionΔABC के अंदर बिंदु O से भुजाओ BC,CA और AB पर क्रमश: लंब OD,OE और OF डाले गए है। सिद्ध कीजिए कि
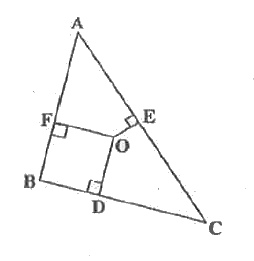
AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2.06:29View SolutionIn Fig. 2.54, o is a point in the interior of a triangle ABC,OD⊥BC,OE⊥ACandof⊥AB. Show that
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2,
 08:10View Solution
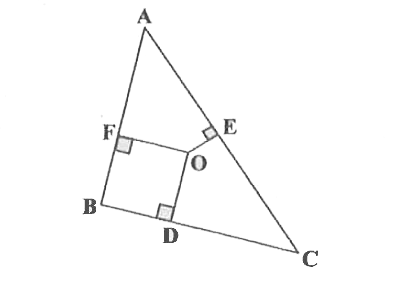
08:10View SolutionIn fig . O is a point in the interior of a triangle ABC , OD ⊥BC,OE⊥ACandOF⊥AB . Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2+AE2+CD2+BF2 .
 07:04View Solution
07:04View Solutionత్రిభుజము ABC అంతరంలో ఏదైనా బిందువు 'O' OD⊥BC,OE⊥AC మరియు OF⊥AB అయిన OA2+OB2+OC2−OD2−OE2−OE2=AE2+BD2+CE2
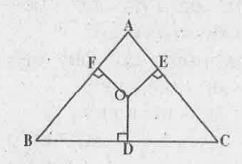 09:25View Solution
09:25View Solutionత్రిభుజము ABC అంతరంలో ఏదైనా బిందువు 'O' OD⊥BC,OE⊥AC మరియు OF⊥AB అయిన AE2+BF2+CD2=AF2+BD2+CE2 అని చూపండి.
 02:18View Solution
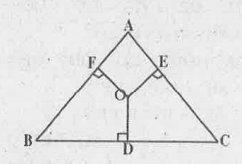
02:18View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
 03:10View Solution
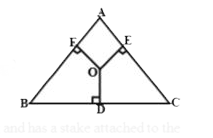
03:10View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
 03:39View Solution
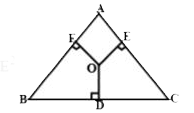
03:39View SolutionIn the given figure, O is a point in the interior of a DeltaABC, OD⊥BC,OE⊥AC and OF⊥AB. Show that :
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2.
 05:32View Solution
05:32View Solution

