In the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
The correct Answer is:20
Topper's Solved these Questions
Similar Questions
Three circles with centres C1,C2andC3 and radii r1,r2andr3 where r1<r2<r3 are placed as shown in the figure
View SolutionCircles C1 and C2 are externally tangent and they are both internally tangent to the circle C_3. The radii of C1 and C2 are 4 and 10, respectively and the centres of the three circles are collinear. A chord of C3 is also a common internal tangent of C1 and C2. Given that the length of the chord is m√np where m,n and p are positive integers, m and p are relatively prime and n is not divisible by the square of any prime, find the value of (m+n+p).
View Solution
Knowledge Check
C1andC2 are two concentric circles with centres at O. Their radii are 12 cm and 3 cm respectively. B is the point of contact of tangents drawn to C2 from a point A lying on the circle C1. Then the area of the triangle OAB is :
A9√152 sq. cmB12√15 sq. cmC9√15 sq. cmD6√15 sq. cmTwo circles with centres at C1,C2 and having radii r1,r2 will intersect each in two real distinct points if , and only if :
Al(C1C2)<r1+r2Bl(C1C2)−|r1−r2|C|r1−r2|<l(C1C2)<r1+r2Dnone of these
Circles C1 and C2 are externally tangent and they are both internally tangent to the circle C3. The radii of C1 and C2 are 4 and 10, respectively and the centres of the three circles are collinear. A chord of C3 is also a common internal tangent of C1 and C2. Given that the length of the chord is m√np where m, n and p are positive integers, m and p are relatively prime and n is not divisible by the square of any prime, find the value of (m + n + p).
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 and C1 Q are in
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
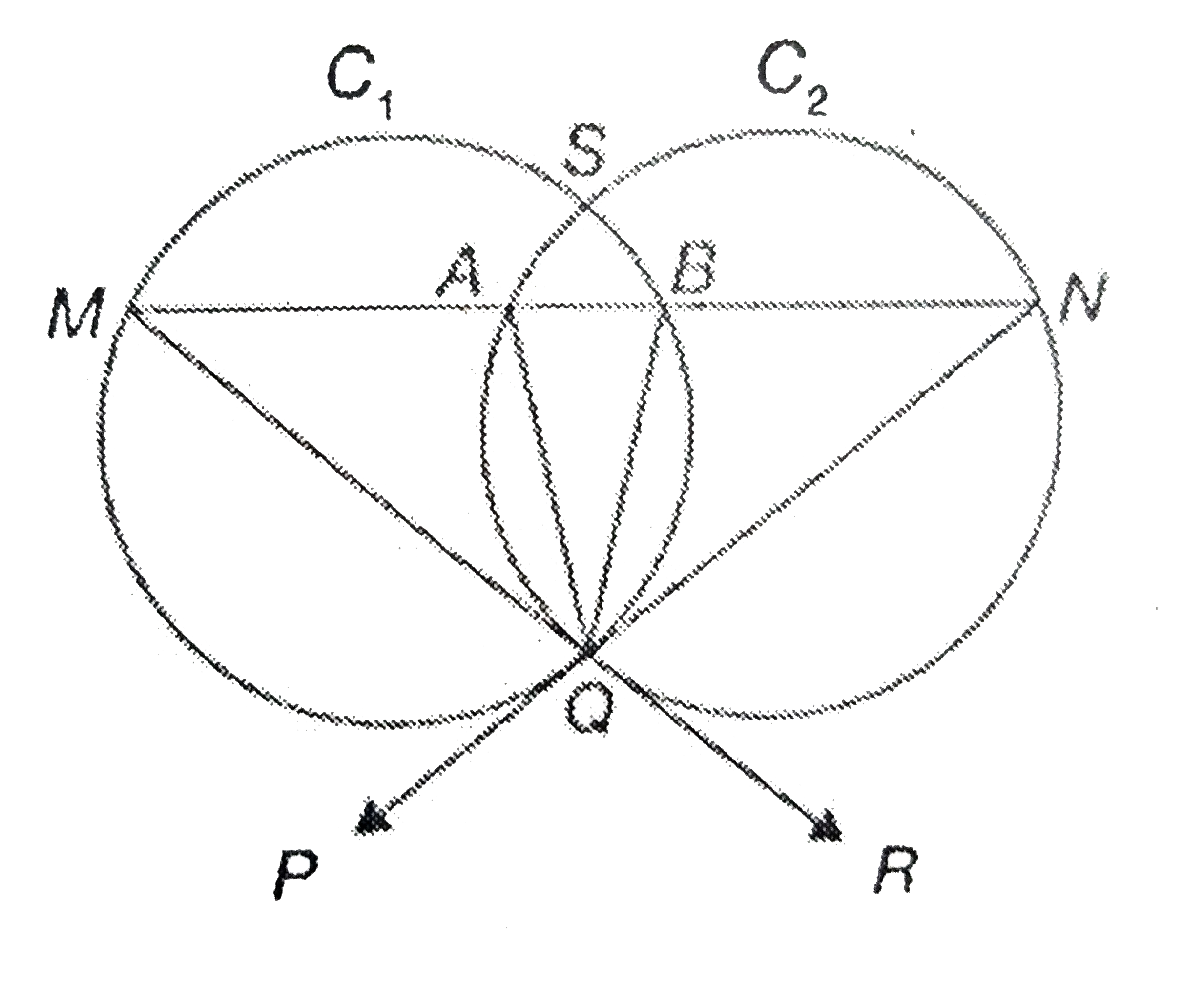
View SolutionIn the given figure (not to scale), two circles C1andC2 intersect at S and Q. PQN and RQM are tangents drawn to C1andC2 respectively at Q. MAB and ABN are the chords of the circles C1andC2. If ∠NQR=85∘, then find ∠AQB.
View SolutionThe line L1≡3x−4y+1=0 touches the circles C1andC2. Centers of C1 and C2 are A1(1,2) and A2(3,1) respectively Then, the length (in units) of the transverse common tangent of C1andC2 is equal to
View SolutionThe line L1≡3x−4y+1=0 touches the circles C1andC2. Centers of C1 and C2 are A1(1,2) and A2(3,1) respectively Then, the length (in units) of the transverse common tangent of C1andC2 is equal to
View Solution
