The internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
To solve the problem, we need to find the relationship between the lengths C1P, C1C2, and C1Q where P is the intersection of the internal tangents and Q is the intersection of the external tangents of two circles with centers C1 and C2.
1. Define the Circles:
Let the center of circle C1 be at the origin (0,0) with radius R1 and the center of circle C2 be at (H,0) with radius R2. The distance between the centers C1 and C2 is C1C2=H.
2. Find the Coordinates of Point P:
The point P, where the internal tangents intersect the line joining C1 and C2, divides the segment C1C2 in the ratio R1:R2. Using the section formula:
P=(R1⋅H+R2⋅0R1+R2,0)=(R1HR1+R2,0)
Therefore, C1P=R1HR1+R2.
3. Find the Coordinates of Point Q:
The point Q, where the external tangents intersect the line joining C1 and C2, divides the segment C1C2 externally in the same ratio R1:R2. Again using the section formula:
Q=(R1⋅H−R2⋅0R1−R2,0)=(R1HR1−R2,0)
Therefore, C1Q=R1HR1−R2.
4. Express the Lengths:
We have:
- C1P=R1HR1+R2
- C1C2=H
- C1Q=R1HR1−R2
5. Reciprocals of the Lengths:
To find the relationship between these lengths, we take the reciprocals:
R1+R2R1H,1H,R1−R2R1H
6. Check for Harmonic Progression:
We need to check if the reciprocals are in harmonic progression (HP). For three quantities a,b,c to be in HP, the condition is:
2b=a+c
Here, let:
- a=R1+R2R1H
- b=1H
- c=R1−R2R1H
Now, we check:
2⋅1H=R1+R2R1H+R1−R2R1H
Simplifying the right-hand side:
(R1+R2)+(R1−R2)R1H=2R1R1H
Thus, we have:
2⋅1H=2R1R1H
This confirms that the three quantities C1P,C1C2,C1Q are in harmonic progression.
Final Result:
The lengths C1P, C1C2, and C1Q are in harmonic progression.
Let the center of circle C1 be at the origin (0,0) with radius R1 and the center of circle C2 be at (H,0) with radius R2. The distance between the centers C1 and C2 is C1C2=H.
The point P, where the internal tangents intersect the line joining C1 and C2, divides the segment C1C2 in the ratio R1:R2. Using the section formula:
P=(R1⋅H+R2⋅0R1+R2,0)=(R1HR1+R2,0)
Therefore, C1P=R1HR1+R2.
The point Q, where the external tangents intersect the line joining C1 and C2, divides the segment C1C2 externally in the same ratio R1:R2. Again using the section formula:
Q=(R1⋅H−R2⋅0R1−R2,0)=(R1HR1−R2,0)
Therefore, C1Q=R1HR1−R2.
We have:
- C1P=R1HR1+R2
- C1C2=H
- C1Q=R1HR1−R2
To find the relationship between these lengths, we take the reciprocals:
R1+R2R1H,1H,R1−R2R1H
We need to check if the reciprocals are in harmonic progression (HP). For three quantities a,b,c to be in HP, the condition is:
2b=a+c
Here, let:
- a=R1+R2R1H
- b=1H
- c=R1−R2R1H
2⋅1H=R1+R2R1H+R1−R2R1H
Simplifying the right-hand side:
(R1+R2)+(R1−R2)R1H=2R1R1H
Thus, we have:
2⋅1H=2R1R1H
This confirms that the three quantities C1P,C1C2,C1Q are in harmonic progression.
The lengths C1P, C1C2, and C1Q are in harmonic progression.
Topper's Solved these Questions
Similar Questions
The internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 and C1 Q are in
View SolutionSuppose that two circles C1 and C2 in a plane have no points in common. Then
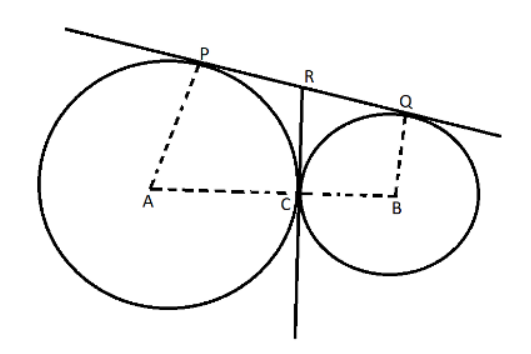
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
View SolutionThe tangent to the curve y=ex drawn at the point (c,ec) intersects the line joining (c−1,ec−1)and(c+1,ec+1) (a) on the left of n=c (b) on the right of n=c (c) at no points (d) at all points
View SolutionFind value of c such that line joining the points (0, 3) and (5, -2) becomes tangent to curve y=cx+1
View SolutionTransverse common tangents are drawn from O to the two circles C1,C2 with 4, 2 respectively. Then the ratio of the areas of triangles formed by the tangents drawn from O to the circles C1andC2 and chord of contacts of O w.r.t the circles C1andC2 respectively is
View SolutionLet C1andC2 are circles defined by x2+y2−20x+64=0 and x2+y2+30x+144=0. The length of the shortest line segment PQ that is tangent to C1 at P and to C2 at Q is
View SolutionLet C1andC2 are circles defined by x2+y2−20x+64=0 and x2+y2+30x+144=0. The length of the shortest line segment PQ that is tangent to C1 at P and to C2 at Q is
View SolutionLet C1andC2 are circles defined by x2+y2−20x+64=0 and x2+y2+30x+144=0. The length of the shortest line segment PQ that is tangent to C1 at P and to C2 at Q is
View Solution
