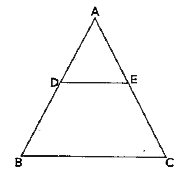
In the figure, sed LM || side BC, AL = x + 3, BL = x - 3, AM = x + 5 and CM = x - 2 then complete the following activity to find the value of x.

Activity :
In ΔABC, sed LM || side BC,
∴ by ________ theorem,
ALLB=AM□
∴x+3x−3=x+5□
∴(x+3)_____=(x+5)(x−3)
x2+x−□=x2+2x−15
∴x=□
Video Solution
Text Solution
In ΔABC, seg LM|| side BC,
∴ by basic proportionality theorem,
ALLB=AMMC
∴x+3x−3=x+5x−2
∴(x+3)(x−2)=(x+5)(x−3)
∴X2+x−6=x2+2x−15
∴X=9
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MODEL QUESTION PAPEREXERCISE - SOLVE ANY TWO OF THE FOLLOWING SUBQUESTIONS:4videos
MODEL QUESTION PAPER
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MODEL QUESTION PAPEREXERCISE - SOLVE ANY TWO THE FOLLOWIN SUBQUESTIONS:3videos
MODEL QUESTION PAPER
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MODEL QUESTION PAPEREXERCISE - SOLVE ANY FOUR THE FOLLOWING SUBQUESTIONS :5videos
MODEL QUESTION PAPER
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MENSURATIONEXERCISE - Assignment 8.58videos
MENSURATION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PRACTICE QUESTION BASEDEXERCISE - STATISTICS13videos
PRACTICE QUESTION BASED
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC, DE || BC. If AD = 2x - 1, AE = 2x + 5, BD = x - 3 and CE = x - 1, then the value of x is:
A8B9C10D11
In ΔABC, when DE || BC and AD = x, DB = 3x + 4, AE = x + 3 and EC = 3x + 19 then value of x is:
 View Solution
View Solutionα and β are the roots of x2−5x−1=0 . Complete the following activity to find the value of x2+β3.
View SolutionIn the figure ΔABC,DE∣∣AB. If AD=2x,DC=x+3,BE=2x−1CE=x then find the value of x.
 View Solution
View SolutionIn figure , DE∣∣BC.If AD=x+1 , DB = x-2 , AE =x+2andEC =x+3 , find the value of x .
 View Solution
View SolutionCompleting the following activity, Evaluate ∫21x+3x(x+2)dx
View SolutionIn the given figure, in ΔABC,DE∣∣BC so that AD=(4x−3)cm,AE=(8x−7)cm,BD=(3x−1)cmandCE=(5x−3)cm . Find the value of x.
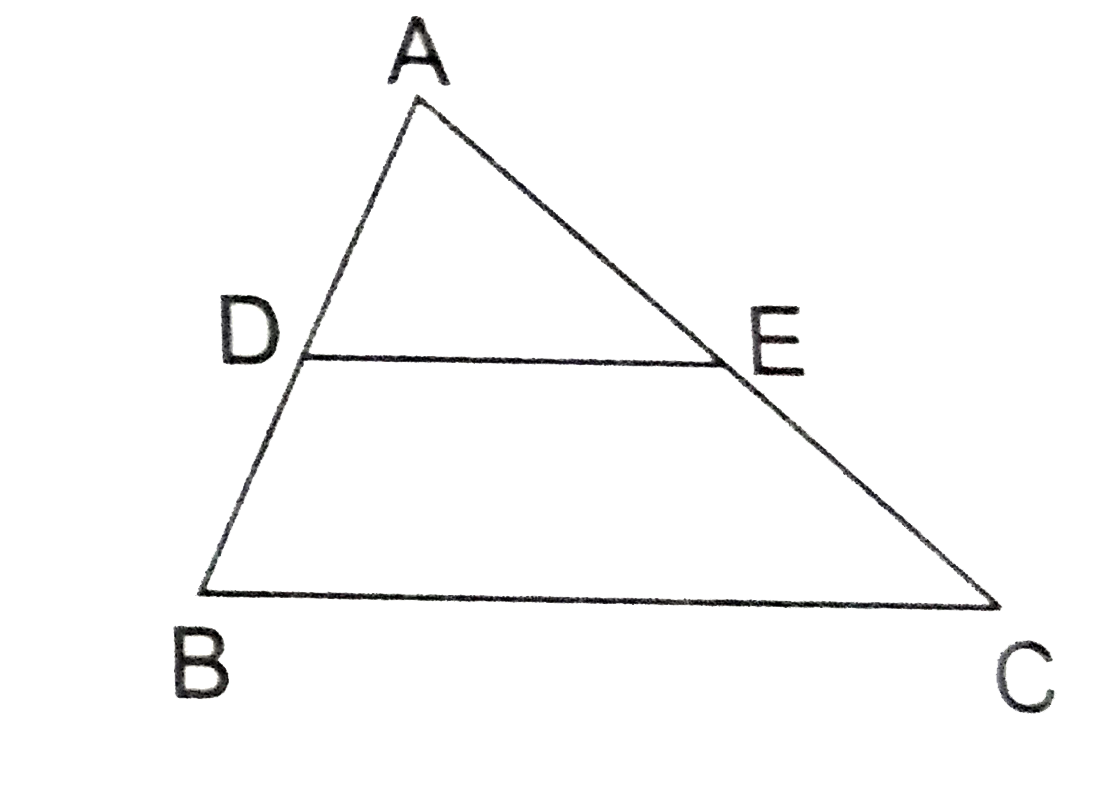
View SolutionIn the given figure, DE∣∣BC such that AD=xcm,DB=(3x+4)cm,AE=(x+3)cmandEC=(3x+19)cm. Find the value of x.
 View Solution
View Solution

