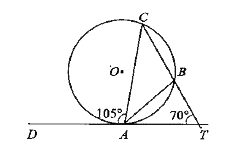
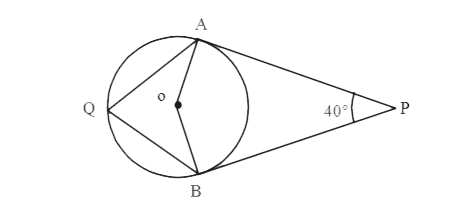
In the figure , TA and TB are tangents to the circles. Find x in both cases.
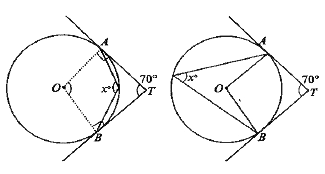
The correct Answer is:x=125∘(b)x=55∘
Topper's Solved these Questions
- TANGENTS TO CIRCLES BOOK - CENGAGECHAPTER - TANGENTS TO CIRCLES EXERCISE - TEST YOURSELF (LEVEL 3)
32 Videos
- TANGENTS TO CIRCLES BOOK - CENGAGECHAPTER - TANGENTS TO CIRCLES EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- TANGENTS TO CIRCLES BOOK - CENGAGECHAPTER - TANGENTS TO CIRCLES EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- STANDARD AND ALLIED ANGLESBOOK - CENGAGECHAPTER - STANDARD AND ALLIED ANGLESEXERCISE - Olympiad And NTSE Level Exercises
10 Videos
- TRANSFORMATIONSBOOK - CENGAGECHAPTER - TRANSFORMATIONSEXERCISE - Olympiad and NTSE level exercises
10 Videos
Similar Questions
Knowledge Check
In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
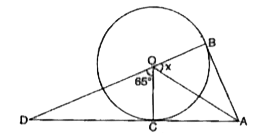 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘TP and TQ are the tangents to a circle, with centre O. Find x.
 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘
In a given figure, TQ and TP are tangents on bigger circle with centre O and TP & TR are tangents on smaller circle with O' then find the ratio of TQ : TR?

View SolutionProve that the length of the tangent drawn from an external point to a circle are equal. Using the above, do the following: TP and TQ are tangents from T to the circle with circle O and R in any point on the circle. If AB is a tangent to the circle at R, prove that TA + AR =TB +BR.

View SolutionIn the given figure PA and PB are tangents to a circle with centre O.If∠APB=(2x+3)∘ and∠AOB=(3x+7)∘ then, find the value of x.
View SolutionIn the given figure PA and PB are tangents to a circle with centre O. if ∠APB=(2x+3)∘ and ∠AOB=(3x+7)∘. then find the value of x.
View SolutionIn the adjoining figure, PA and PB are tangents from P to a circle with center C.If the radius of the circle is 4 cm and PA perpendicular PB.Find the length of the tangent.
View SolutionIn the given figure, PT is a tangent to the circle with centre O. If OT=6cm and OP=10cm, thcn find the length of tangent PT.
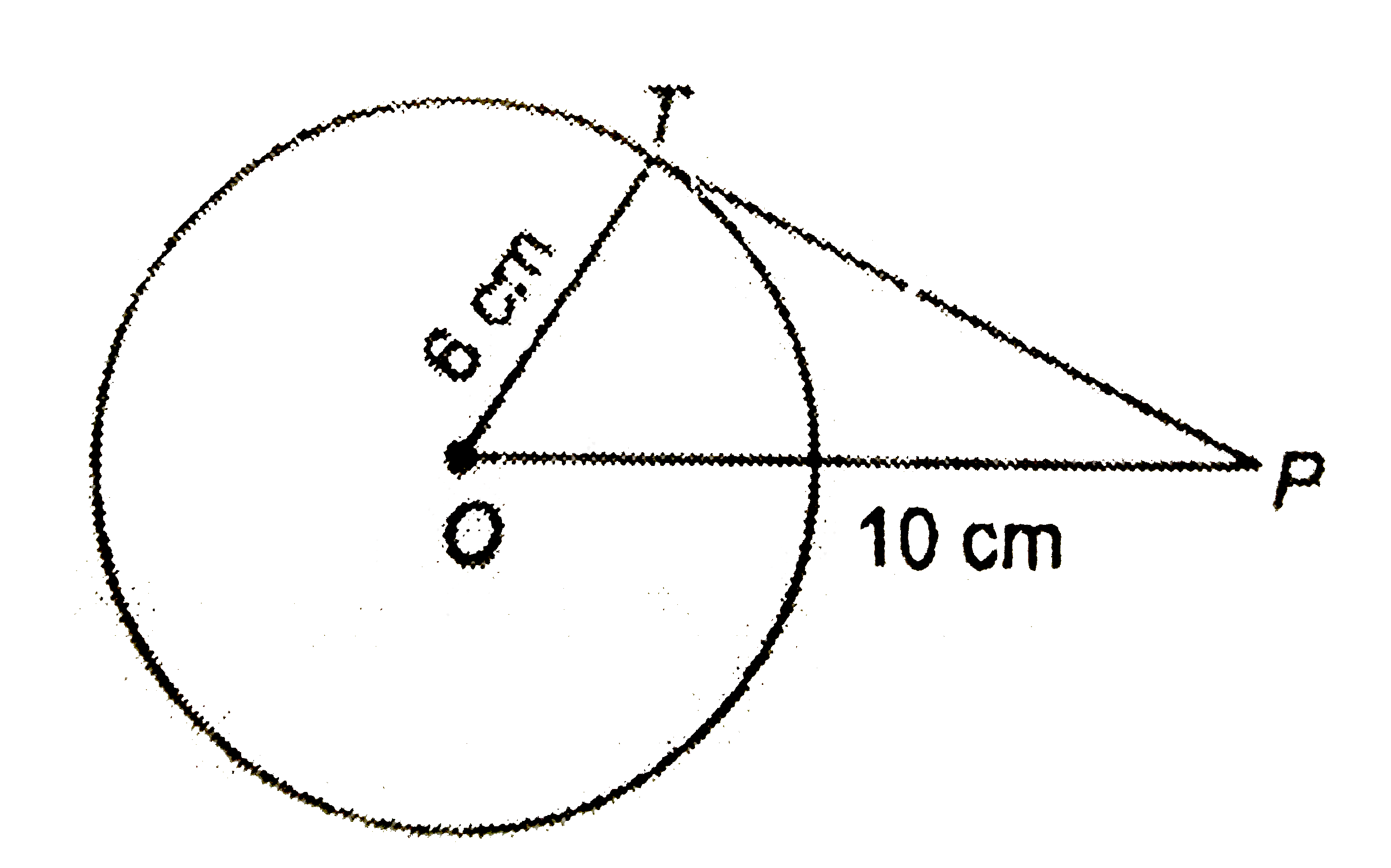
View Solution