In the figure △ABC~△AED. If AD=5 cm , AE= 6 cm, BC= 12 cm and AB = 15 cm. Determine AC and DE.
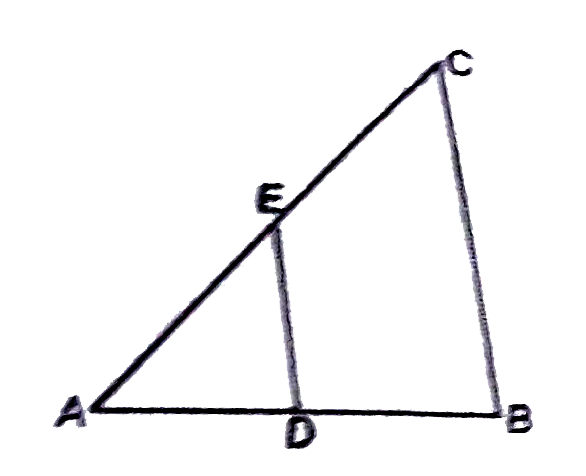
The correct Answer is:11.2 cm
Step by step video & image solution for In the figure triangleABC~triangleAED. If AD=5 cm , AE= 6 cm, BC= 12 cm and AB = 15 cm. Determine AC and DE. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6c
10 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6d
27 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In △ABC right angled at C. AB= 1.7 cm, BC= 1.5 cm, find CA
View SolutionIn the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE
View SolutionIn ΔABC,∠ABC=∠DAC,AB=8cm,AC=4cmandAD=5cm.

Find BC and CD.
View SolutionIn the given figure AD is the bisector of ∠A. If BD= 4 cm , DC = 3 cm and AB = 6cm . Find AC.

View SolutionIn given figure, if ∠A=∠C, AB= 6 cm, BP = 15 cm, AP = 12 cm and CP= 4 cm, then find the lengths of PD and CD.

View SolutionThe following figures shows a right - angled triangle ABC with ∠B=90∘,AB=15 cm and AC = 25 cm. D is a point in side BC and CD = 7 cm. if De ⊥AC, find the length of DE.

View SolutionIn ΔABC,∠ABC=∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
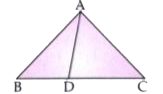
(ii) Find the length of BC and CD.
View SolutionIn the given figure, DE//BC,AE=15cm,EC=9cm,NC=6cmandBN=24cm.
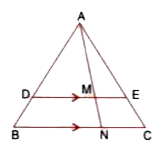
Find lengths of ME and DM.
View SolutionIn the figure given below, AB // EF // CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
AC

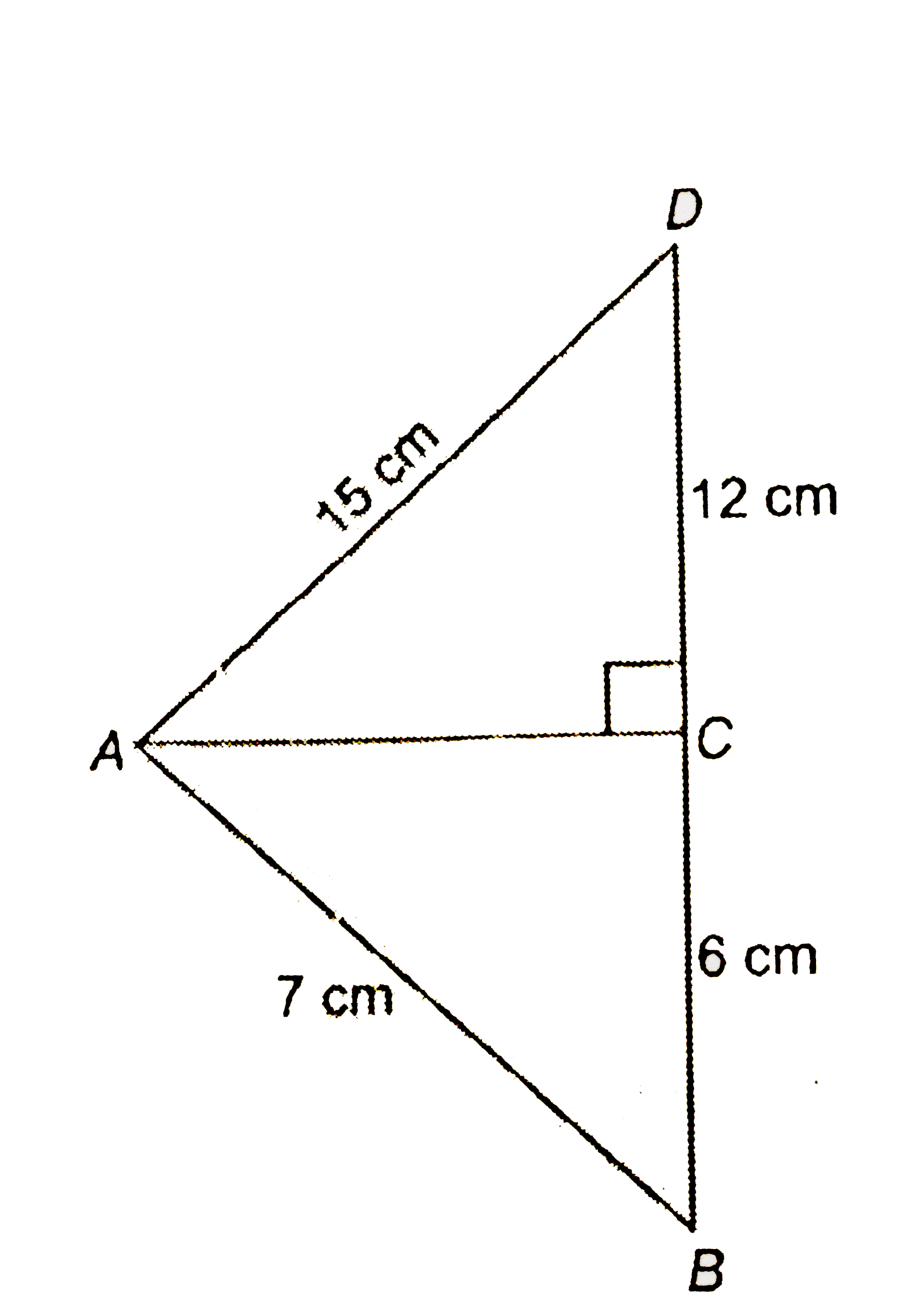
View SolutionIn the given figure ∠ACD=90∘
Ad=15 cm, DC=12 cm, AB=7 cm and BC=6 cm
Find the are of the shaded region.
View Solution
