D is a point on the side BC of △ABC such that ∠ADC=∠BAC, prove that CA2=CB×CD.
Step by step video & image solution for D is a point on the side BC of triangleABC such that angleADC= angleBAC, prove that CA^(2)=CBxxCD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
D is a point on the side BC of a triangle ABC such that ∠ADC=∠BAC. Show that CA2=CB.CD.
View SolutionIf D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
View SolutionP is any point inside the triangle ABC. Prove that : ∠BPC>∠BAC.
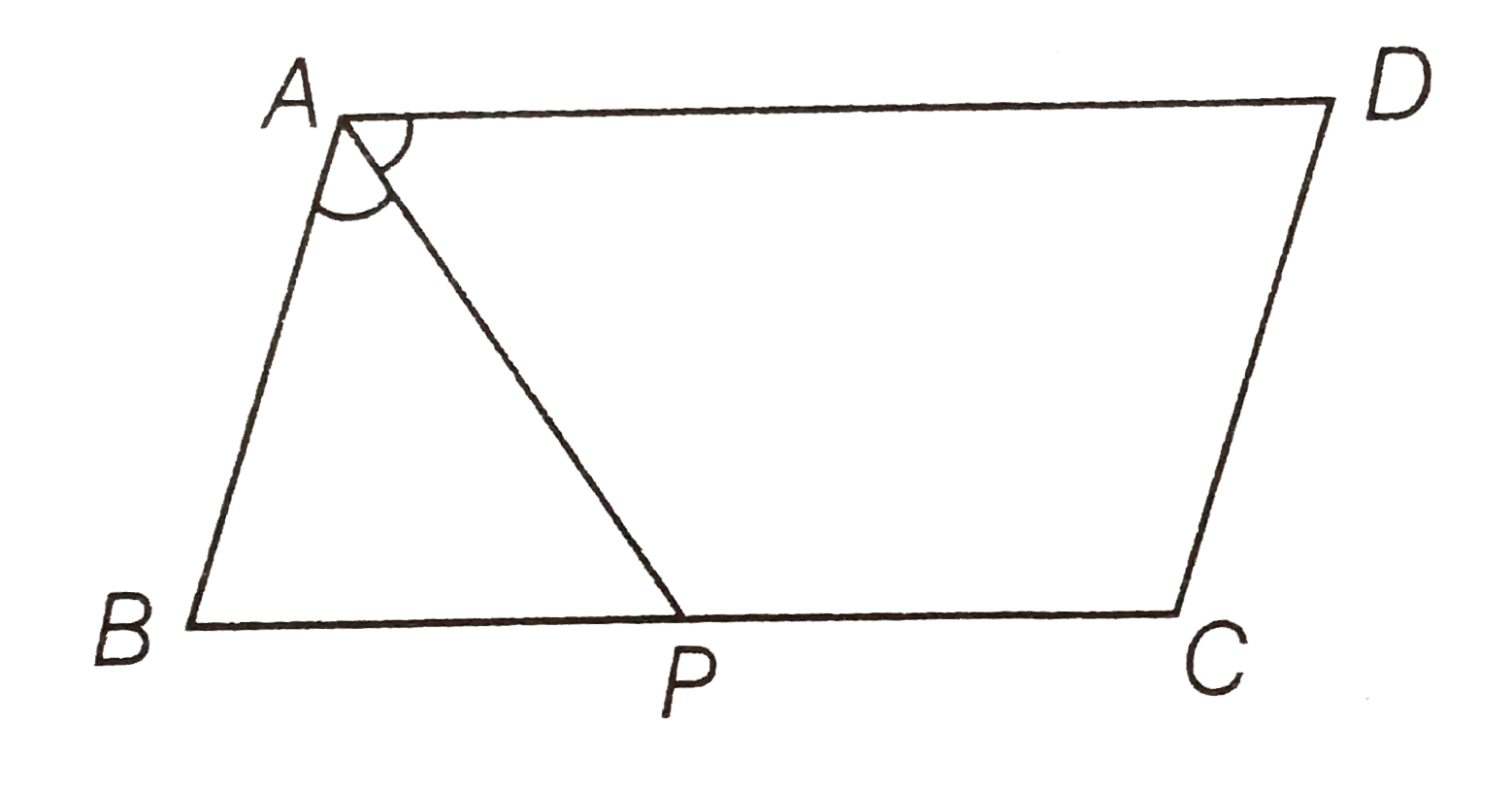
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2+BD2=AB2+DE2 .
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2+BD2=AB2+DE2.
View SolutionIn figure D is a point on side BC of a ΔABCsuch that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.

View SolutionX and Y are points on the sides AB and BC respectively of △ABC such that XY||AC and XY divides △ABC into two parts in area , find AXAB
View SolutionIn △ABC,∠A=60∘ prove that BC2=AB2+AC2−AB.AC
View SolutionLex X by any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA meeting CA, BA in M, N respectively; MN meets BC produced in T, prove that TX2=TB x TC
View Solution
