In the formula ∠A+∠B+∠C=180∘, if ∠A=90∘ and ∠B=55∘, then ∠C=____________ (a) π4 (b) π6 (c) π3 (d) none of these
π/4
π/6
π/3
none of these
The correct Answer is:3
To solve the problem, we need to find the value of angle C given the values of angle A and angle B. We know that the sum of the angles in a triangle is 180 degrees.
1. Write the equation for the sum of angles:
angle A+angle B+angle C=180∘
2. Substitute the known values:
Given that angle A = 90° and angle B = 55°, we substitute these values into the equation:
90∘+55∘+angle C=180∘
3. Combine the known angles:
Add angle A and angle B:
145∘+angle C=180∘
4. Isolate angle C:
To find angle C, subtract 145° from both sides:
angle C=180∘−145∘
angle C=35∘
5. Convert angle C to radians:
To convert degrees to radians, we use the conversion factor π180∘:
angle C=35∘×π180∘
Simplifying this gives:
angle C=35π180=7π36
6. Check the options:
The options provided are:
(a) π4
(b) π6
(c) π3
(d) none of these
Since 7π36 does not match any of the options, the correct answer is:
angle C=7π36(option d: none of these)
Final Answer:
angle C=7π36 (d) none of these.
---
angle A+angle B+angle C=180∘
Given that angle A = 90° and angle B = 55°, we substitute these values into the equation:
90∘+55∘+angle C=180∘
Add angle A and angle B:
145∘+angle C=180∘
To find angle C, subtract 145° from both sides:
angle C=180∘−145∘
angle C=35∘
To convert degrees to radians, we use the conversion factor π180∘:
angle C=35∘×π180∘
Simplifying this gives:
angle C=35π180=7π36
The options provided are:
(a) π4
(b) π6
(c) π3
(d) none of these
angle C=7π36(option d: none of these)
angle C=7π36 (d) none of these.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Multiple correct answers type48videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Numerical Value Type24videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.75videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Find ∠A+∠B+∠C+∠D
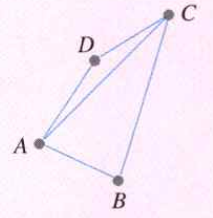 View Solution
View SolutionIn ΔABC,∠A−∠B=16∘and∠C−∠A=34∘=34∘ , find all angles of the triangle
View SolutionIn ΔABC,∠B=90∘,∠A=30∘,b=20cm, find a and c.
View SolutionIn a ΔABC,∠A=2∠B=3∠C, find each of the triangle.
View SolutionIn a △ABC,∠B=900andb+a=4. The area of the triangle is maximum when ∠C is (a)π4 (b) π6 (c)π3 (d) none of these
View SolutionIf tan−1(cotθ)=2 θ , then θ= (a) ±π3 (b) ±π4 (c) ±π6 (d) none of these
View SolutionIn ΔABC,∠A=x+15∘,∠B=xand∠C=2x−35∘ find, each angle of the triangle.
View SolutionIn a triangle ∠A=55∘,∠B=15∘,∠C=110∘. Then c2−a2 is equal to
View SolutionGiven : In quadrilateral ABCD, ∠C=64∘,∠D=∠C−8∘,∠A=5(a+2)∘and∠B=2(2a+7)∘. Calculate ∠A.
View SolutionABCD is a cyclic quadrilateral such that ∠A=90∘,∠B=70∘,∠C=95∘and∠D=105∘.
View Solution

