In a find each of the triangle.
The correct Answer is:
To solve the problem, we need to find the angles of triangle ABC given the relationships between the angles: ∠A=2∠B and ∠A=3∠C.
1. Set Up the Relationships:
We know from the problem statement that:
- ∠A=2∠B (1)
- ∠A=3∠C (2)
2. Express Angles in Terms of Angle B:
From equation (1), we can express ∠A in terms of ∠B:
∠A=2B
From equation (2), we can express ∠C in terms of ∠B:
∠C=23∠B
3. Use the Angle Sum Property:
The sum of the angles in a triangle is always 180 degrees:
∠A+∠B+∠C=180
Substituting the expressions for ∠A and ∠C:
2B+B+23B=180
4. Combine Like Terms:
Combine the terms on the left side:
3B+23B=180
To combine 3B and 23B, we convert 3B into a fraction:
3B=93B
Now we can add:
93B+23B=113B
So we have:
113B=180
5. Solve for Angle B:
Multiply both sides by 311:
B=180×311=54011
Converting this to a mixed number:
B=49111 degrees
6. Find Angle A:
Using ∠A=2B:
A=2×54011=108011
Converting to a mixed number:
A=98211 degrees
7. Find Angle C:
Using ∠C=23B:
C=23×54011=36011
Converting to a mixed number:
C=32811 degrees
Final Angles:
- ∠A=98211 degrees
- ∠B=49111 degrees
- ∠C=32811 degrees
We know from the problem statement that:
- ∠A=2∠B (1)
- ∠A=3∠C (2)
From equation (1), we can express ∠A in terms of ∠B:
∠A=2B
From equation (2), we can express ∠C in terms of ∠B:
∠C=23∠B
The sum of the angles in a triangle is always 180 degrees:
∠A+∠B+∠C=180
Substituting the expressions for ∠A and ∠C:
2B+B+23B=180
Combine the terms on the left side:
3B+23B=180
To combine 3B and 23B, we convert 3B into a fraction:
3B=93B
Now we can add:
93B+23B=113B
So we have:
113B=180
Multiply both sides by 311:
B=180×311=54011
Converting this to a mixed number:
B=49111 degrees
Using ∠A=2B:
A=2×54011=108011
Converting to a mixed number:
A=98211 degrees
Using ∠C=23B:
C=23×54011=36011
Converting to a mixed number:
C=32811 degrees
- ∠A=98211 degrees
- ∠B=49111 degrees
- ∠C=32811 degrees
Topper's Solved these Questions
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Revision Exercise (very Short Answer Questions )
Explore 10 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Revision Exercise (short Answer Questions)
Explore 12 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Exercise 6 B
Explore 16 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Revision Exercise
Explore 12 Videos
- NUMBER SYSTEMBook:NAGEEN PRAKASHAN ENGLISHChapter:NUMBER SYSTEMExercise:Revision Exercise (short Answer Questions)
Explore 10 Videos
Similar Questions
In ΔABC,∠A=600,∠B=45∘, find a:b.
View SolutionIn ΔABC,∠A=x+15∘,∠B=xand∠C=2x−35∘ find, each angle of the triangle.
View SolutionA triangle ABC is such that 3∠A=4∠B=6∠C. Find the three angles.
View SolutionIn ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12A
View SolutionIn ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12
View SolutionFind ∠A+∠B+∠C+∠D
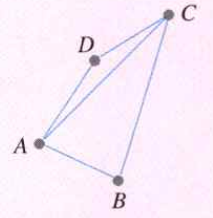
View SolutionIn ΔABC,∠A=60∘,∠B=90∘,∠C=30∘. Let H be its orthocentre, then :
(where symbols used have usual meanings)
View SolutionIn ΔABCandΔPQR , If AB=AC, ∠C=∠P and ∠B=∠Q, then the two triangles are
View SolutionΔABC , ∠A+∠B=65∘, ∠B+∠C=140∘,then ∠B is equal to
View SolutionIn ΔABC,∠C=40∘,BQandAR are the angle bisectors of ∠Band∠A, respectively. Find ∠APQ.
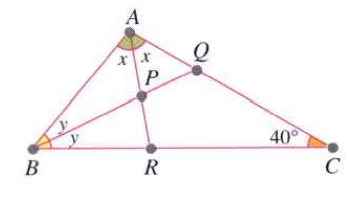
View Solution
