In the given figure, AB is diameter of the circle with centre O. AQ, BP and PRQ are tangents. Prove that OP and OQ are perpendicular to each other.
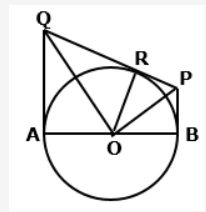
Step by step video & image solution for In the given figure, AB is diameter of the circle with centre O. AQ, BP and PRQ are tangents. Prove that OP and OQ are perpendicular to each other. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
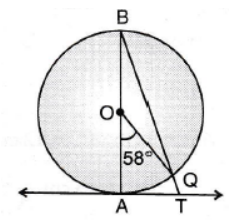
In the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
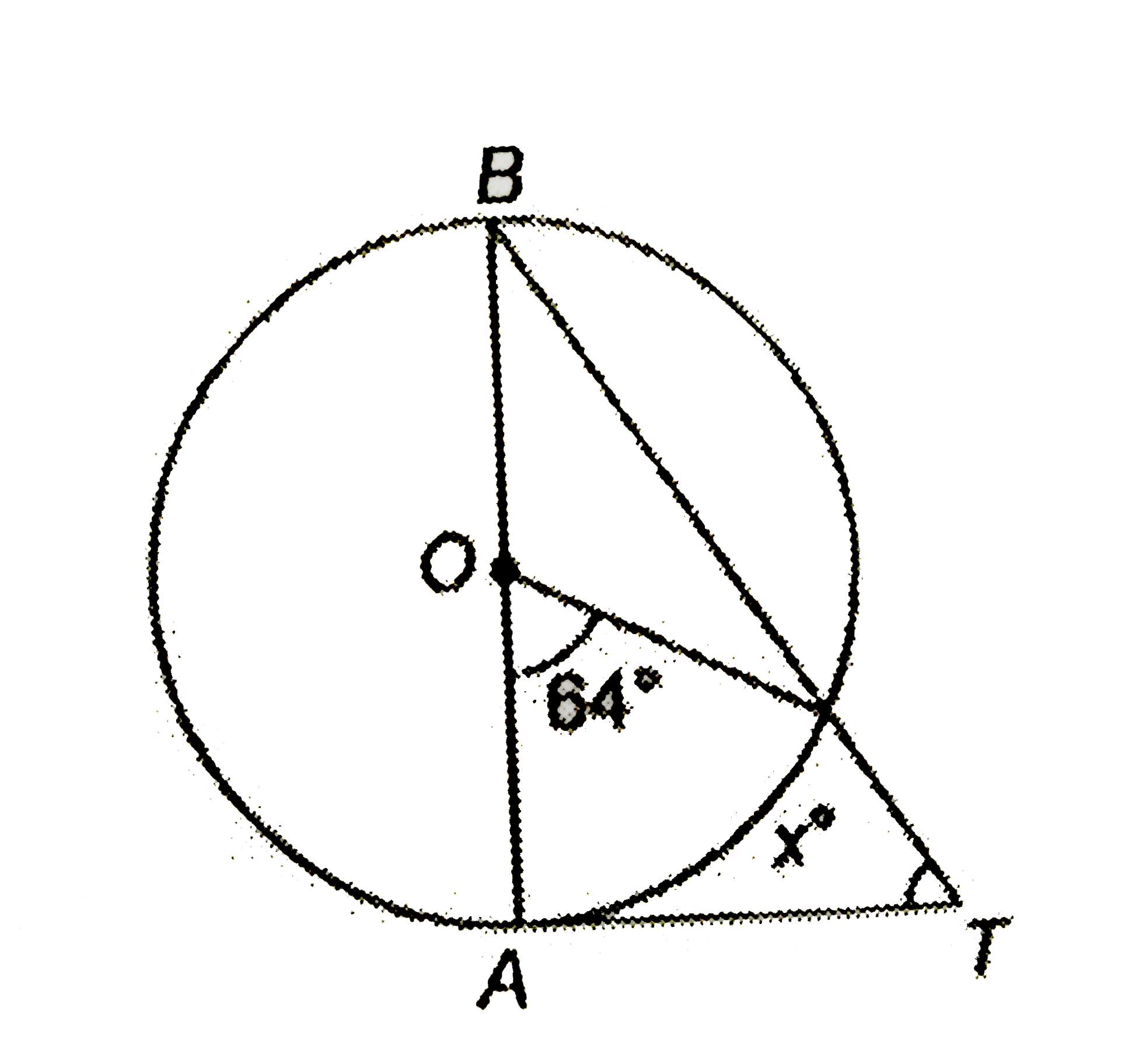
View SolutionIn the giben figure, AB is the diameter of the circle, with centre O and AT is the tangent. Calculate the calue of x.
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
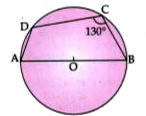
∠BCD=130∘. Find
(i) ∠DAB
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
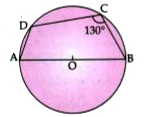
∠BCD=130∘. Find
(ii) ∠DBA
View SolutionIn the figure, PO⊥QO. The tangents to the circle with centre O at P and Q intersect at a point T. Prove that PQ and OT are right bisectors of each other.

View SolutionIn the given figure, PA and PB are tangents to a circle with centre O. Prove that ∠APB and ∠AOB are supplementary.

View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
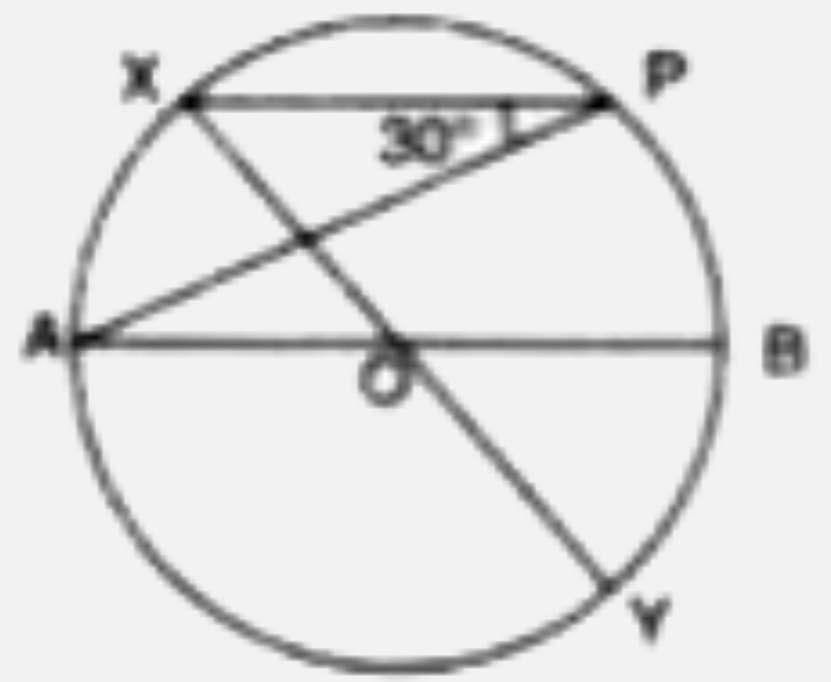
∠AOX
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:

∠APY
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
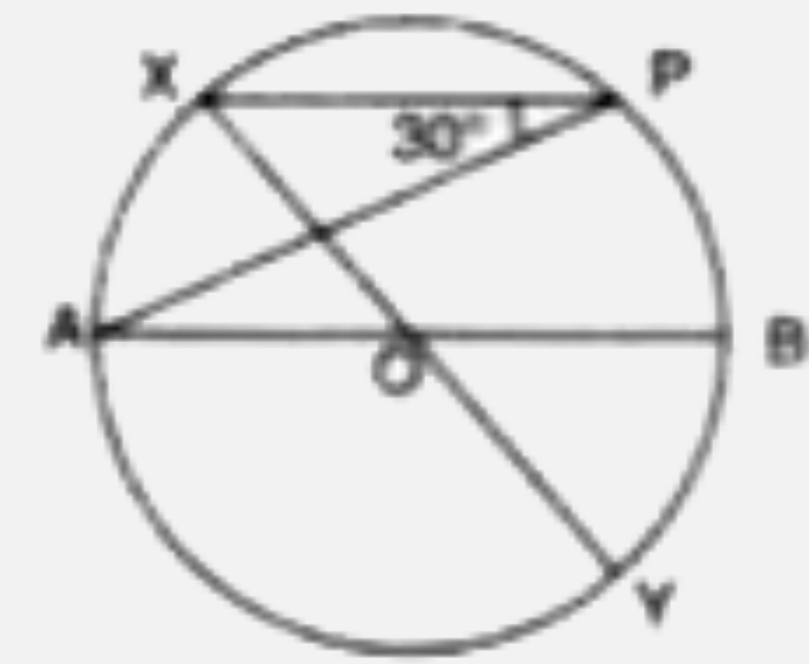
∠BPY
View Solution
